Vous êtes ici

Corrigé BFEM maths 2014

Exercice 1

Dans une petite et moyenne entreprise ou $PMI$ on étudie la répartition des salaires des travailleurs.

Le schéma ci-dessous représente l'histogramme des $E.C.C$ et celui des $E.C.D$ tracés dans un même repère.

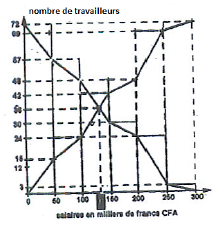
1) D'après le schéma :

a) le caractère étudié est le salaire des travailleurs. Il est de nature quantitative.

b) on décompte 72 travailleurs dans cette $PMI.$

c) 48 travailleurs gagnent au moins $100\:000\;F\;CFA.$

d) 42 travailleurs gagnent moins de $150\:000\;F\;CFA.$

e) 6 travailleurs gagnent entre $150\:000\;F\ $ et $\ 200\:000\;F.$

2) Histogramme des effectifs cumulés croissants

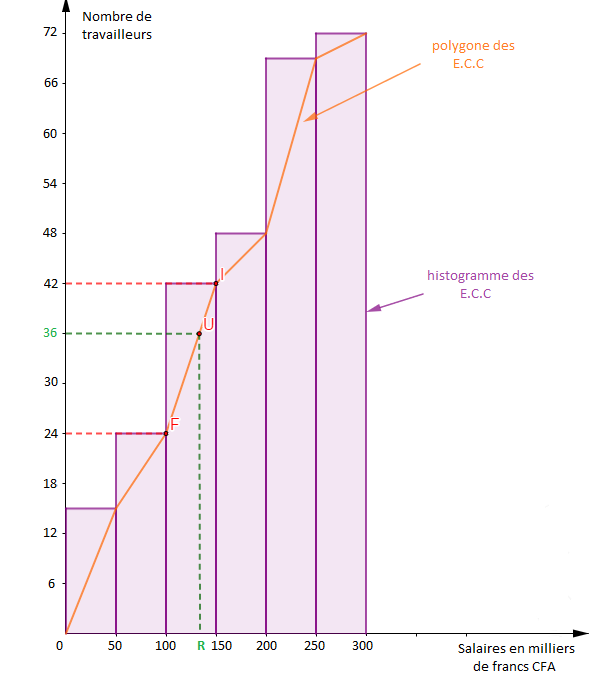
$$\begin{array}{rcl}\text{Échelle }:\ 1\;cm&\longrightarrow&50\:000\;F\\ 0.5\;cm&\longrightarrow&3\text{ travailleurs} \end{array}$$

3) Le salaire $R$ constitue la médiane de la série statistique étudiée. Ce salaire sépare alors la population des travailleurs en deux groupes de même effectif.

4) Calculons la valeur de $R$

$R$ étant la médiane donc, $R$ est l'abscisse du point $U$ d'ordonnée 36.

De plus, on constate que $R\in\;[100\;;\ 150[$ et que $U\in\;[FI]$

On a : $U\in\;[FI]$ alors, les points $F\;,\ U\ $ et $\ I$ sont alignés.

Donc, les vecteurs $\overrightarrow{FI}\begin{pmatrix} 150-100\\42-24\end{pmatrix}\ $ et $\ \overrightarrow{FU}\begin{pmatrix} R-100\\36-24\end{pmatrix}\ $ sont colinéaires.

On a : $\overrightarrow{FI}\begin{pmatrix} 50\\18\end{pmatrix}\ $ et $\ \overrightarrow{FU}\begin{pmatrix} R-100\\12\end{pmatrix}$ colinéaires si, et seulement si, $$50\times 12-18\times(R-100)=0$$

Soit alors, $600-18\times R+1800=0$

Ce qui donne : $18\times R=2400$

d'où, $R=\dfrac{2400}{18}=133.333$

Ainsi, $\boxed{R=133\:000\;F\;CFA}$ à 1 millier de francs près par défaut.

Exercice 2

On donne les réels : $$a=5-2\sqrt{5}\quad b=1+\dfrac{2}{5}\sqrt{5}\quad\text{et}\quad c=\dfrac{-5}{5+2\sqrt{5}}$$

1) Justifions que $a\ $ et $\ b$ sont des inverses l'un de l'autre.

On a : $a$ et $b$ sont inverses si, et seulement si, $a\times b=1$

Donc, calculons le produit $a\times b$

On a :

$\begin{array}{rcl} a\times b&=&(5-2\sqrt{5})\left(1+\dfrac{2}{5}\sqrt{5}\right)\\ \\&=&5\times 1+5\times\dfrac{2}{5}\sqrt{5}-1\times 2\sqrt{5}-(2\sqrt{5})\times\left(\dfrac{2}{5}\sqrt{5}\right) \\\\&=&5+2\sqrt{5}-2\sqrt{5}-4\\\\&=&5-4\\\\&=&1\end{array}$

Ainsi, $a\times b=1$, d'où $a\ $ et $\ b$ sont inverses.

2) Justifions que $a\ $ et $\ c$ sont opposés.

$a\ $ et $\ c$ sont opposés si, et seulement si, $c=-a$ ou encore $a+c=0.$

On a : $c=\dfrac{-5}{5+2\sqrt{5}}$

Rendons rationnel le dénominateur en le multipliant par son expression conjuguée.

On obtient :

$\begin{array}{rcl} c&=&\dfrac{-5}{5+2\sqrt{5}}\\ \\&=&\dfrac{-5(5-2\sqrt{5})}{(5+2\sqrt{5})(5-2\sqrt{5})}\\ \\&=&\dfrac{-25+10\sqrt{5}}{5^{2}-(2\sqrt{5})^{2}}\\ \\&=&\dfrac{-25+10\sqrt{5}}{25-20}\\ \\&=&\dfrac{-25+10\sqrt{5}}{5}\\ \\&=&-5+2\sqrt{5}\ =\ -(5-2\sqrt{5})\end{array}$

donc, on voit bien que $c=-a$

Ce qui montre alors que $a\ $ et $\ c$ sont opposés.

3) Justifions que $c=-\dfrac{1}{b}$

On a : $b=1+\dfrac{2}{5}\sqrt{5}$

donc, en réduisant au même dénominateur on obtient :

$\begin{array}{rcl} b&=&1+\dfrac{2}{5}\sqrt{5}\\ \\&=&\dfrac{5}{5}+\dfrac{2}{5}\sqrt{5}\\ \\&=&\dfrac{5+2\sqrt{5}}{5}\end{array}$

ainsi, $\dfrac{1}{b}=\dfrac{1}{\dfrac{5+2\sqrt{5}}{5}}\ $ or, on sait que $\dfrac{1}{\dfrac{N}{D}}=\dfrac{D}{N}$

par suite : $\dfrac{1}{\dfrac{5+2\sqrt{5}}{5}}=\dfrac{5}{5+2\sqrt{5}}$

ce qui donne alors, $\dfrac{1}{b}=\dfrac{5}{5+2\sqrt{5}}$

par conséquent, $-\dfrac{1}{b}=\dfrac{-5}{5+2\sqrt{5}}=c$

Ce qui montre bien que $c=-\dfrac{1}{b}$

4) Justifions que $b\times c+1=0.$

On a : $c=-\dfrac{1}{b}$ donc, $c\times b=-1$

En ajoutant 1 à chaque membre on obtient :

$c\times b+1=-1+1=0$

5) Encadre $c$ à $10^{-2}$ près sachant que $2.236<\sqrt{5}<2.237$

On a :

$\begin{array}{rcccl} 2.236&<&\sqrt{5}&<&2.237\\ 2\times 2.236&<&2\times\sqrt{5}&<&2\times 2.237\\ 5+2\times 2.236&<&5+2\times\sqrt{5}&<&5+2\times 2.237\\ 9.472&<&5+2\times\sqrt{5}&<&9.474\end{array}$

alors, en inversant chaque membre tout en changeant le sens des inégalités, on obtient : $$\dfrac{1}{9.474}<\dfrac{1}{5+2\sqrt{5}}<\dfrac{1}{9.472}$$

Ce qui donne, après multiplication de chaque membre par $(-5)$, sachant que là encore les inégalités changent de sens : $\dfrac{-5}{9.472}<\dfrac{-5}{5+2\sqrt{5}}<\dfrac{-5}{9.474}$

Soit alors : $-0.5278<\dfrac{-5}{5+2\sqrt{5}}<-0.5277$

Par conséquent, un encadrement de $c$ à $10^{-2}$ près sera donné par : $$-0.53<c<-0.52$$

Exercice 3

1) Faisons une figure

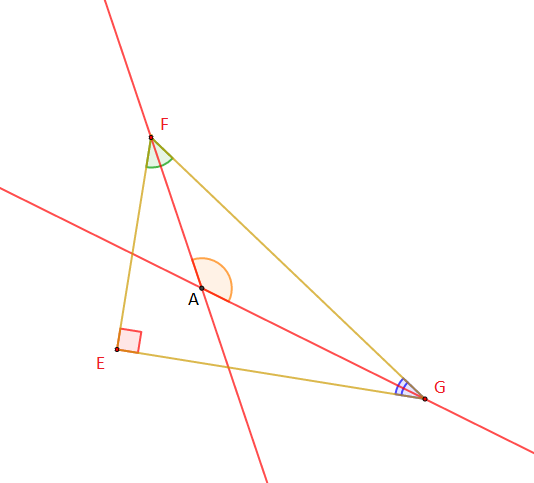
2) Calculons la mesure de l'angle $\widehat{FAG}.$

On sait que dans un triangle rectangle les angles aigus sont complémentaires.

Donc : $$\widehat{EFG}+\widehat{EGF}=90^{\circ}$$

Aussi, dans un triangle la somme des angles fait $180^{\circ}.$

Donc, en considérant le triangle $FAG$ on aura : $$\widehat{AFG}+\widehat{AGF}+\widehat{FAG}=180^{\circ}$$

Or, $\widehat{AFG}=\dfrac{1}{2}\widehat{EFG}\ $ et $\ \widehat{AGF}=\dfrac{1}{2}\widehat{EGF}$

ainsi,

$\begin{array}{rcl} \widehat{FAG}&=&180^{\circ}-(\widehat{AFG}+\widehat{AGF})\\ \\&=&180^{\circ}-\left(\dfrac{1}{2}\widehat{EFG}+\dfrac{1}{2}\widehat{EGF}\right)\\ \\&=&180^{\circ}-\dfrac{1}{2}(\widehat{EFG}+\widehat{EGF})\quad\text{or },\ \widehat{EFG}+\widehat{EGF}=90^{\circ}\\ \\&=&180^{\circ}-\dfrac{1}{2}90^{\circ}\\ \\&=&180^{\circ}-45^{\circ}\ =\ 135^{\circ}\end{array}$

D'où, $\boxed{\widehat{FAG}=135^{\circ}}$

Exercice 4

Une bougie décorative a la forme d'un cône de révolution de sommet $S$, de hauteur $27\;cm.$ Sa base est un disque de centre $O$ et de rayon $15\;cm.$

Cette bougie est formée de trois parties de couleurs différentes séparées par des plans parallèles au plan de sa base et qui coupent sa hauteur respectivement en $M\ $ et $\ N$ tels que $$SM=MN=ON$$

1) a) Montre que la longueur $SM=9\;cm$

On a : $SO=SM+MN+NO\ $ or, $\ SM=MN=ON$

donc, $SO=3SM\ $ d'où : $SM=\dfrac{SO}{3}=\dfrac{27}{3}$

Par conséquent, $SM=9\;cm$

Justifions que le cône de hauteur $SM$ est une réduction de la bougie de coefficient $\dfrac{1}{3}$

En effet, le cône de hauteur $SM$ est obtenu en sectionnant la bougie parallèlement au plan de sa base. Donc, c'est une réduction de la bougie.

Son coefficient de réduction est donné par $$k=\dfrac{SM}{SO}=\dfrac{9}{27}=\dfrac{1}{3}$$

b) Calculons le coefficient de réduction du cône de hauteur $SN.$

Le cône de hauteur $SN$ étant une réduction de la bougie alors, le coefficient de réduction est donné par $k'=\dfrac{SN}{SO}.$

Or, on sait que $SN=SM+MN\ $ et que $\ SM=SN=9\;cm$

Donc, $SN=9+9=18\;cm$

Ainsi, $k'=\dfrac{18}{27}=\dfrac{2}{3}$

2) a) Montre que le rayon de la base du cône de hauteur $SM$ est $5\;cm.$

On sait que dans le cadre d'une réduction de coefficient $k$ les distances sont multipliées par $k$ donc, si $R$ est le rayon de base de la bougie et $r$ celui du cône de hauteur $SM$ alors, on aura : $$r=k\times R$$

Ainsi, $r=\dfrac{1}{3}\times 15=5\;cm$

Ce qui montre que le rayon de la base du cône de hauteur $SM$ est $5\;cm.$

b) Calcule son volume $\mathcal{V}_{1}$

On sait que $$\mathcal{V}_{\text{cône}}=\dfrac{1}{3}\times\pi\times(\text{Rayon de base})^{2}\times(\text{Hauteur})$$

Donc,

$\begin{array}{rcl} \mathcal{V}_{1}&=&\dfrac{1}{3}\times\pi\times r^{2}\times SM\\ \\&=&\dfrac{1}{3}\times\pi\times(5)^{2}\times(9)\\ \\&=&\dfrac{3.14\times 25\times 9}{3}\\ \\&=&235.5\end{array}$

D'où : $\boxed{\mathcal{V}_{1}=235.5\;cm^{3}}$

3) a) Calculons le volume $\mathcal{V}_{2}$ de la partie intermédiaire.

Soit $\mathcal{V}'$ le volume du cône de hauteur $SN$ et de rayon de base $r'.$

On a :

$\begin{array}{rcl} \mathcal{V}'&=&\dfrac{1}{3}\times\pi\times r'^{2}\times SN\quad\text{avec }r'=k'\times R=\dfrac{2}{3}\times 15=10\\ \\&=&\dfrac{1}{3}\times\pi\times(10)^{2}\times(18)\\ \\&=&\dfrac{3.14\times 100\times 18}{3}\\ \\&=&1884\end{array}$

Donc, $\mathcal{V}'=1884\;cm^{3}$

Alors,

$\begin{array}{rcl} \mathcal{V}_{2}&=&\mathcal{V}'-\mathcal{V}_{1}\\\\&=&1884-235.5\\\\&=&1648.5\end{array}$

D'où : $\boxed{\mathcal{V}_{2}=1648.5\;cm^{3}}$

b) Calculons le volume $\mathcal{V}_{3}$ de la partie inférieure.

Calculons d'abord le volume total $\mathcal{V}$ de cette bougie.

On a :

$\begin{array}{rcl} \mathcal{V}&=&\dfrac{1}{3}\times\pi\times R^{2}\times SO\\ \\&=&\dfrac{1}{3}\times\pi\times(15)^{2}\times(27)\\ \\&=&\dfrac{3.14\times 225\times 27}{3}\\ \\&=&6358.5\end{array}$

Donc, $\mathcal{V}=6358.5\;cm^{3}$

Par suite, on aura :

$\begin{array}{rcl}\mathcal{V}_{3}&=&\mathcal{V}-(\mathcal{V}_{1}+\mathcal{V}_{2})\\\\&=&6358-(235.5+1648.5)\\\\&=&6358.5-1884\\\\&=&4474.5\end{array}$

Ainsi, $\boxed{\mathcal{V}_{3}=4474.5\;cm^{3}}$

c) Exprimons $\mathcal{V}_{2}$ et $\mathcal{V}_{3}$ en fonction de $\mathcal{V}_{1}.$

On a : $\mathcal{V}_{2}=\mathcal{V}'-\mathcal{V}_{1}\ $ or $\ \mathcal{V}'=k'^{3}\mathcal{V}\ $ et $\ \mathcal{V}_{1}=k^{3}\mathcal{V}\ $ car dans le cas d'une réduction de coefficient $k$ les volumes sont multipliés par $k^{3}.$

De ces dernières égalités on tire : $\ \mathcal{V}=\dfrac{1}{k^{3}}\mathcal{V}_{1}$

Ainsi,

$\begin{array}{rcl}\mathcal{V}_{2}&=&\mathcal{V}'-\mathcal{V}_{1}\\\\&=&k'^{3}\mathcal{V}-\mathcal{V}_{1}\\ \\&=&\dfrac{k'^{3}}{k^{3}}\mathcal{V}_{1}-\mathcal{V}_{1}\\ \\&=&\left(\dfrac{k'}{k}\right)^{3}\mathcal{V}_{1}-\mathcal{V}_{1}\\ \\&=&\left(\dfrac{\dfrac{2}{3}}{\dfrac{1}{3}}\right)^{3}\mathcal{V}_{1}-\mathcal{V}_{1}\\ \\&=&8\mathcal{V}_{1}-\mathcal{V}_{1}\\ \\&=&7\mathcal{V}_{1}\end{array}$

D'où : $\boxed{\mathcal{V}_{2}=7\mathcal{V}_{1}}$

Aussi, on a : $\mathcal{V}_{3}=\mathcal{V}-(\mathcal{V}_{1}+\mathcal{V}_{2})\ $ or $\ \mathcal{V}=\dfrac{1}{k^{3}}\mathcal{V}_{1}\ $ et $\ \mathcal{V}_{2}=7\mathcal{V}_{1}$

Donc,

$\begin{array}{rcl}\mathcal{V}_{3}&=&\mathcal{V}-(\mathcal{V}_{1}+\mathcal{V}_{2})\\\\&=&\dfrac{1}{k^{3}}\mathcal{V}_{1}-\left(\mathcal{V}_{1}+7\mathcal{V}_{1}\right)\\ \\&=&\dfrac{1}{\left(\dfrac{1}{3}\right)^{3}}\mathcal{V}_{1}-8\mathcal{V}_{1}\\ \\&=&27\mathcal{V}_{1}-8\mathcal{V}_{1}\\ \\&=&19\mathcal{V}_{1}\end{array}$

Ainsi, $\boxed{\mathcal{V}_{3}=19\mathcal{V}_{1}}$

Auteur:

Diny Faye