Corrigé BFEM Maths 2011
Exercice 1
1) $m=1-2\sqrt{3}$ ; montrons que $m$ est négatif.
On sait que $1^{2}=1\;;\ \left(2\sqrt{3}\right)^{2}=2^{2}\times\left(\sqrt{3}\right)^{2}=4\times 3=12.$
Puisque $1<12$ alors, $1^{2}<\left(2\sqrt{3}\right)^{2}.$
Or, 1 est un réel positif et $2\sqrt{3}$ est un réel positif donc, $1<2\sqrt{3}.$
D'où, $1-2\sqrt{3}<0$
Ce qui montre que $m$ est négatif.
2) $m=1-2\sqrt{3}$ ; calculons $m^{2}$
On a :
$\begin{array}{rcl} m^{2}&=& \left(1-2\sqrt{3}\right)^{2}\\&=& 1^{2}-2\times 1\times 2\sqrt{3}+\left(2\sqrt{3}\right)^{2}\\&=& 1-4\sqrt{3}+4\times 3\\&=&13-4\sqrt{3}\end{array}$
Donc, $\boxed{m^{2}=13-4\sqrt{3}}$
Déduisons-en que $p$ et$m$ sont opposés.
On a : $m^{2}=13-4\sqrt{3}\ $ et $\ p=\sqrt{13-4\sqrt{3}}$ donc, $p=\sqrt{m^{2}}=|m|.$
Or, $m$ est négatif donc, $p=-m$
Ce qui signifie que $p$ et$m$ sont opposés.
3) Encadrement de $m\ $ à $\ 10^{-2}$ près
On sait que $1.732<\sqrt{3}<1.733$
donc, $-2\times 1.732>-2\times\sqrt{3}>-2\times 1.733$
par suite, $-3.466<-2\sqrt{3}<-3.464\ $ et $\ -3.466+1<1-2\sqrt{3}<-3.464+1$
ainsi, $-2.466<1-2\sqrt{3}<-2.464$
D'où $-2.47<1-2\sqrt{3}<-2.46$
4) $p=\sqrt{13-4\sqrt{3}}\ $ et $\ q=\sqrt{13+4\sqrt{3}}$ ; montrons que $p\times q=11$
On a :
$\begin{array}{rcl} p\times q&=&\sqrt{13-4\sqrt{3}}\times\sqrt{13+4\sqrt{3}}\\&=&\sqrt{13^{2}-\left(4\sqrt{3}\right)^{2}}\\&=&\sqrt{169-48}\\&=& \sqrt{121}\\&=&11\end{array}$
Donc, $\boxed{p\times q=11}$
Exercice 2
1) Montrons qu'il a 50 lutteurs dans cette écurie
On a :$$\text{Pourcentage d'une modalité}=\dfrac{\text{Effectif partiel d'une modalité}\times 100}{\text{Effectif total de la population}}$$
alors $$\text{Effectif total}=\dfrac{\text{Effectif partiel d'une modalité}\times 100}{\text{Pourcentage d'une modalité}}$$
or l'effectif partiel de la classe $[95\;;\ 110[$ est 6 et le pourcentage correspondant est 12 donc : Effectif total de la population est égal à $\dfrac{6}{12}\times 100=50.$
Il y a donc 50 lutteurs dans cette classe.
2) Montrons que le nombre de lutteurs de la classe $[110\;;\ 125[$ est 5
On a ; dans un diagramme circulaire
$$\text{Angle d'une modalité}=\dfrac{360^{\circ}\times\text{Effectif partiel de la modalité}}{\text{Effectif total de la population}}$$
alors
$$\text{Effectif partiel}=\dfrac{\text{Angle de la modalité}\times\text{Effectif total de la population}}{360^{\circ}}$$
or, l'angle de la représentation de la classe $[110\;;\ 125[$ dans le diagramme circulaire de la série est $36^{\circ}$ et l'effectif total de l'écurie est 50 donc l'effectif partiel de cette classe est égal à $\dfrac{36^{\circ}\times 50}{360^{\circ}}=5$
3) Vérifions que la classe $[125\;;\ 140[$ compte 15 lutteurs
On a :
$$\text{Effectif partiel d'une modalité}=\text{Fréquence d'une modalité}\times\text{Effectif total}$$
Or la fréquence de la classe $[125\;;\ 140[$ est $0.3$ et l'effectif total est 50 donc
$$\text{Effectif partiel}=0.3\times 50=15$$
4) Montrons qu'il y a 6 lutteurs dans la classe $[140\;;\ 155[$
Calculons l'effectif total de lutteurs dans les classes $[95\;;\ 110[\;,\ [110\;;\ 125[$ et $[125\;;\ 140[\ :$
on a : $6+5+15=26$
or, l'effectif total est 50 alors le nombre de lutteurs dans les classes $[80\;;\ 95[$ et $[140\;;\ 155[$ est $50-26=24$
Soit $x$ l'effectif de la classe $[80\;;\ 95[$ donc l'effectif de la classe $[140\;;\ 155[$ est $\dfrac{x}{3}$
Par conséquent, $x+\dfrac{x}{3}=24$ alors $\dfrac{3x+x}{3}=24$ donc $x=18$
D'où, l'effectif de la classe $[80\;;\ 95[$ est 18 et l'effectif de la classe $[140\;;\ 155[$ est $\dfrac{18}{3}=6$
Établissons le tableau des effectifs cumulés croissants
$$\begin{array}{|c|c|c|c|c|c|}\hline\text{Classe de poids} & [80\;;\ 95[ & [95\;;\ 110[ & [110\;;\ 125[ & [125\;;\ 140[ & [140\;;\ 155[ \\ \hline\text{Effectifs} & 18 & 6 & 5 & 15 & 6 \\ \hline\text{Effectif cumulé} & 18 & 24 & 29 & 44 & 50 \\ \text{croissant} & & & & & \\ \hline\end{array}$$
La moitié de l'effectif total est $\dfrac{50}{2}=25.$
Donc, d'après la ligne des effectifs cumulés croissants 25 apparient à la classe $[110\;;\ 125[.$
Par conséquent, la classe médiane est la classe $[110\;;\ 125[.$
Exercice 3
1) $(D_{1})\ :\ y=-x+1\;;\ \vec{u}(1\;;\ -1)\;;\ \vec{u}$ est un vecteur directeur de $(D_{1})$
$(D_{2})\ :\ x-y+3=0\;;\ \vec{v}(-(-1)\;;\ 1)\;;\ \vec{v}$ est un vecteur directeur de $(D_{2})$
$\vec{u}\ $ et $\ \vec{v}$ sont orthogonaux si, et seulement si, $$x_{\vec{u}}.x_{\vec{v}}+y_{\vec{u}}.y_{\vec{v}}=0$$
On a : $1\times 1+(-1)\times 1=1-1=0$
donc, les vecteurs $\vec{u}\ $ et $\ \vec{v}$ sont orthogonaux.
Par conséquent, les droites $(D_{1})$ et $(D_{2})$ sont perpendiculaires.
Autre Méthode : utiliser le produit des coefficients directeurs qui est égal à $-1.$
2) a) Construisons les droites $(D_{1})$ et $(D_{2})$ dans un repère orthonormal $(O\;;\ I\;;\ J)$
Soit $(D_{1})\ :\ y=-x+1$
Si $x=0$ alors $y=1\;,\quad A(0\;;\ 1)$
Si $x=1$ alors $y=0\;,\quad B(1\;;\ 0)$
Soit $(D_{2})\ :\ x-y+3=0$
Si $x=0$ alors $y=3\;,\quad C(0\;;\ 3)$
Si $x=1$ alors $y=4\;,\quad D(1\;;\ 4)$
Plaçons les points $A\;,\ B\;,\ C$ et $D$ dans le repère orthonormal.
$(D_{1})$ passe par les points $A$ et $B$ et $(D_{2})$ passe par les ponts $C$ et $D$
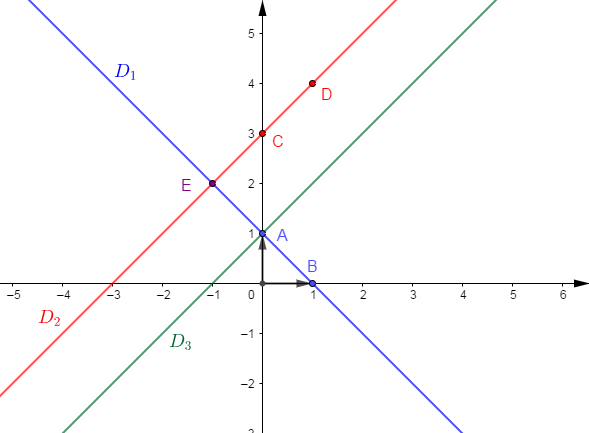
b) $(D_{1})\ :\ y=-x+1$ et $J(0\;;\ 1)$
on a $-0+1=1$ donc $J\in(D_{1})$
c) Le point $E$, point d'intersection des droites $(D_{1})$ et $(D_{2})$, a pour couple de coordonnées le couple de réels solution du système d'équations formé par les équations de droites $(D_{1})$ et $(D_{2})$
$$\left\lbrace\begin{array}{rcl} y &=& -x+1 \\ x-y+3 &=& 0\end{array}\right.$$ résolvons ce système $\left\lbrace\begin{array}{rcl} x+y-1 &=& 0 \\ x-y+3 &=& 0\end{array}\right.$
En additionnant les deux équations on obtient alors, $2x+2=0$
donc, $x=-1\ $ et $\ y=-(-1)+1=2$
Le couple de réels $(-1\;;\ 2)$ est solution du système d'équations.
D'où, $E(-1\;;\ 2)$
d) Calculons la distance $EJ$
On a :
$\begin{array}{rcl} EJ&=&\sqrt{(0-(-1))^{2}+(1-2)^{2}}\\&=&\sqrt{1+1}\\&=&\sqrt{2}\end{array}$
e) Déterminons une équation de la droite $(D_{3})$ passant par $J$ et parallèle à $(D_{2})$
$(D_{2})\ :\ x-y+3=0\;;\quad (D_{2})\ :\ y=x+3$ le coefficient directeur de $(D_{2})$ est 1.
La droite $(D_{3})$ est parallèle à la droite $(D_{2})$ donc elle a le même coefficient directeur 1.
Par conséquent, $(D_{3})\ :\ y=x+b$
or, $J(0\;;\ 1)\in(D_{3})$ donc, $1=0+b$
par suite, $b=1$
Ainsi, $(D_{3})\ :\ y=x+1$
f) Déterminons la position relative de $(D_{3})\ $ et $\ (D_{1})$
Les droites $(D_{3})\ $ et $\ (D_{1})$ sont parallèles et la droite $(D_{1})$ est perpendiculaire à $(D_{2})$ donc, $(D_{1})$ est perpendiculaire à $(D_{3})$
Autre Méthode : le produit de leur coefficient directeur est $-1$
Exercice 4
On considère la figure codée ci-dessous
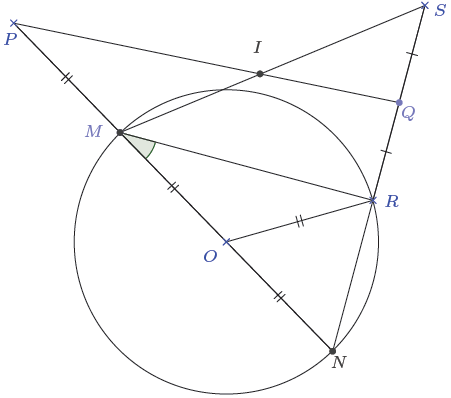
$MR=8\;cm\;;\ NR=6\;cm$
1) Le segment $[MN]$ est un diamètre du cercle et $R$ est un point du cercle donc le triangle $MNR$ est rectangle en $R.$
Autre Méthode : D'après le codage le point $O$ est milieu de $[MN]$ et le point $O$ est à égale distance des trois sommets du triangle $NRM$ donc le triangle $NRM$ est rectangle en $R.$
Autre Méthode : Le point $O$ est le milieu de $[MN]$ et $O$ est le centre du cercle dont l'angle au centre $\widehat{MON}$ est un angle plat et mesure $180^{\circ}.$
$\widehat{MRN}$ est un angle inscrit qui intercepte le même arc de cercle que l'angle au centre $\widehat{MON}$
donc,
$\begin{array}{rcl} {MRN}&=&\dfrac{\widehat{MON}}{2}\\ \\ &=&\dfrac{180^{\circ}}{2}\\ \\&=&90^{\circ}\end{array}$
d'où, $MRN$ est un triangle rectangle en $R.$
2) Calculons $MN$
Le triangle $NRM$ est rectangle en $R$ alors, d'après le théorème de Pythagore on a :
$\begin{array}{rcl} MN^{2}&=&MR^{2}+NR^{2}\\&=&8^{2}+6^{2}\\&=&64+36\\&=&100\end{array}$
donc, $\boxed{MN=10\;cm}$
3) Calculons $\tan\widehat{RMN}$
On a :
$\begin{array}{rcl}\tan\widehat{RMN}&=&\dfrac{NR}{MR}\\ \\&=&\dfrac{6}{8}\\ \\&=&0.75\end{array}$
donc, $\boxed{\tan\widehat{RMN}=0.75}$
4) Démontrons que $I$ est le milieu de $[MS]$
Les points $N\;,\ R\;,\ Q$ et $S$ sont alignés et $NRM$ est un triangle rectangle en $R$ donc $(MR)$ est perpendiculaire à $(RS).$
D'après le codage $(IQ)$ est perpendiculaire à $(RS)$ et $Q$ est milieu de $[RS].$
$(MR)$ est perpendiculaire à $(RS)$ et $(IQ)$ est perpendiculaire à $(RS)$ donc $(MR)$ est parallèle à $(IQ).$
$MRS$ est un triangle ; $Q$ est le milieu de $[RS]$ ; $(MR)$ est parallèle à $(IQ)$ et $I\in[MS]$ donc, d'après le théorème de la droite des milieux $I$ est le milieu de $[MS]$
Autre Méthode : utiliser le théorème de Thalès avec les triangles $SIQ$ et $SMR$ qui sont en position de Thalès
$\dfrac{SI}{SM}=\dfrac{SQ}{SR}$
or, $\dfrac{SQ}{SR}=\dfrac{1}{2}$
donc, $SI=\dfrac{1}{2}SM$
d'où, $I$ est le milieu de $[MS]$
5) Montrons que $NQ=9\;cm$
$(MR)$ parallèle à $(IQ)$ et $P\in(IQ)$ donc, $(MR)$ parallèle à $(PQ)$
$R\in[NQ]$ et $M\in[NP]$ donc, $(MR)$ parallèle à $(PQ)$
Par conséquent, les triangles $NRM$ et $NPQ$ sont en position de Thalès.
D'après le théorème de Thalès on a : $\dfrac{NR}{NQ}=\dfrac{NM}{NP}$ alors, $NR\times NP=NM\times NQ$
D'où, $NQ=\dfrac{NR\times NP}{NM}$
D'après le codage $NO=OM=MP$
or, $NO=\dfrac{MN}{2}=\dfrac{10}{2}=5\;cm$ et $NP=NO+OM+MP$
donc, $NP=3\times NO=3\times 5=15\;cm$
Par conséquent,
$\begin{array}{rcl} NQ&=&\dfrac{NR\times NP}{NM}\\ \\&=&\dfrac{6\times 15}{10}\\ \\&=&\dfrac{90}{10}\\ \\&=&9\;cm\end{array}$
6) Démontrons que la droite $(OR)$ est parallèle à la droite $(MS)$
Calculons les rapports $\dfrac{NR}{NS}$ et $\dfrac{NO}{NM}$
$NR=6\;cm$ et $NM=10\;cm$ calculons les distances $NO$ et $NS$
$O$ est le milieu de $[MN]$
donc,
$\begin{array}{rcl} NO&=&\dfrac{MN}{2}\\ \\&=&\dfrac{10}{2}\\ \\&=&5\;cm\end{array}$
$R\in[NQ]\;;\ NR=6\;cm$ et $NQ=9\;cm$
donc, $RQ=NQ-NR=9\;cm-6\;cm=3\;cm$
$Q$ est le milieu de $[RS]$ et $RQ=3\;cm$
donc, $RS=2\times 3=6\;cm$ et $NS=NR+RS=6+6=12\;cm$
ainsi, $NS=12\;cm$
$\begin{array}{rcl} \dfrac{NR}{NS}&=&\dfrac{6}{12}\\ \\&=&\dfrac{1}{2}\end{array}\quad\text{ et }\quad\begin{array}{rcl} \dfrac{NO}{NM}&=&\dfrac{5}{10}\\ \\&=&\dfrac{1}{2}\end{array}$
donc, $\dfrac{NR}{NS}=\dfrac{NO}{NM}$
Les points $N\;,\ R$ et $S$ d'une part et les points $N\;,\ O$ et $P$ d'autre part sont alignés dans le même ordre et $\dfrac{NR}{NS}=\dfrac{NO}{NM}$ donc d'après la réciproque du théorème de Thalès les droites $(OR)$ et $(MS)$ sont parallèles.
Auteur:
Abdoulaye Ba

Commentaires
Anonyme (non vérifié)
jeu, 01/21/2021 - 21:17
Permalien
Merci pour votre réponse
Anonyme (non vérifié)
jeu, 01/21/2021 - 21:18
Permalien
Merci pour votre réponse
Anonyme (non vérifié)
ven, 06/21/2024 - 18:12
Permalien
Vous avez trompé au niveau d
Ajouter un commentaire