Corrigé BFEM maths 2010
Exercice 1
Le schéma ci-dessous représente le patron d'un cône de révolution de sommet $S$, de rayon de base $r.$
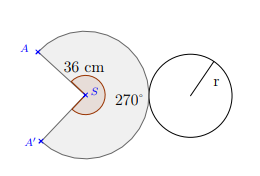
La génératrice $[SA]$ a pour longueur $36\;cm.$
1) Justifions que la circonférence de sa base mesure $54\pi\;cm$
Soit $p$ le périmètre de base de la cône.
On constate alors que la longueur de l'arc $\overset{\displaystyle\frown}{AA'}$ est égale au périmètre de la base du cône.
Or, la longueur de l'arc $\overset{\displaystyle\frown}{AA'}$ est donnée par :
$$\overset{\displaystyle\frown}{AB}=SA\times mes\,\hat{S}$$
Donc, $p=SA\times 270^{\circ}$
Par ailleurs,
$\begin{array}{rcl} 270^{\circ}&=&180^{\circ}+90^{\circ}\\ \\&=&\pi+\dfrac{\pi}{2}\\ \\&=&\dfrac{2\pi+\pi}{2}\\ \\&=&\dfrac{3\pi}{2}\end{array}$
Donc, $270^{\circ}=\dfrac{3\pi}{2}$
Puis, en remplaçant dans l'expression de $p$, on obtient :
$\begin{array}{rcl} p&=&SA\times\dfrac{3\pi}{2}\\ \\&=&36\times\dfrac{3\pi}{2}\\ \\&=&\dfrac{108\pi}{2}\\ \\&=&54\pi\end{array}$
D'où, $\boxed{p=54\pi\;cm}$
2) Montrons que son rayon de base $r$ vaut $27\;cm$
Soit $p=2\pi r\ \Rightarrow\ r=\dfrac{p}{2\pi}$
Or, $p=54\pi\;cm$ donc, $r=\dfrac{54\pi}{2\pi}=27$
Ainsi, $\boxed{r=27\;cm}$
3) Justifions que la hauteur de ce cône est égale à $9\sqrt{7}\;cm$
En considérant la figure ci-dessous représentant le cône, on voit que la génératrice $[SA]$, la hauteur $h=SO$ et le rayon $r=OA$ forment un triangle rectangle $SOA$ en $O.$
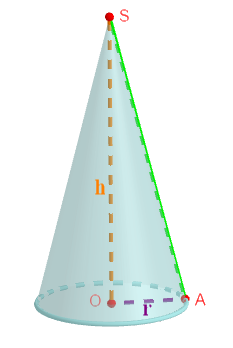
Donc, d'après le théorème de Pythagore, on a :
$$SA^{2}=SO^{2}+OA^{2}$$
Par suite,
$\begin{array}{rcrcl} SO^{2}=SA^{2}-OA^{2}&\Rightarrow&SO&=&\sqrt{SA^{2}-OA^{2}}\\ \\&\Rightarrow&SO&=&\sqrt{(36)^{2}-(27)^{2}}\\ \\&\Rightarrow&SO&=&\sqrt{1296-729}\\ \\&\Rightarrow&SO&=&\sqrt{567}\\ \\&\Rightarrow&SO&=&\sqrt{81\times 7}\\ \\&\Rightarrow&SO&=&9\sqrt{7}\end{array}$
D'où, $\boxed{h=SO=9\sqrt{7}\;cm}$
4) Calculons l'aire totale de ce cône.
Soit : $\mathcal{A}$ l'aire totale du cône alors, on a :
$$\mathcal{A}=\mathcal{A}_{_{L}}+\mathcal{A}_{_{B}}$$
avec, $\mathcal{A}_{_{L}}=\pi\times SA\times r$ aire latérale et $\mathcal{A}_{_{B}}=\pi\times r^{2}$ aire de base.
Par suite,
$\begin{array}{rcl}\mathcal{A}&=&\pi\times SA\times r+\pi\times r^{2}\\ \\&=&3.14\times 36\times 27+3.14\times(27)^{2}\\ \\&=&3052.08+2289.06\\ \\&=&5341.14\end{array}$
Ainsi, $\boxed{\mathcal{A}=5341.14\;cm^{2}}$
Exercice 2
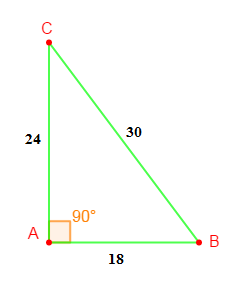
$ABC$ est un triangle rectangle en $A$ tel que :
$$AB+AC+BC=72\;cm\text{ et }4AB=3AC$$
1) Sans calculer les longueurs des côtés du triangle $ABC$,
a) montrons que $7AB+3BC=216\;cm$
On a : $AB+AC+BC=72\;cm$ donc, en multipliant cette relation par $3$, on obtient :
$\begin{array}{rcl} 3\times(AB+AC+BC)=3AB+3AC+3BC&=&3\times 72\;cm\\ \\&=&216\;cm\end{array}$
Ainsi, $3AB+3AC+3BC=216\;cm$
Or, par hypothèse on a : $3AC=4AB$ donc, en remplaçant dans la dernière relation, on trouve :
$\begin{array}{rcrcl} 3AB+3AC+3BC=216\;cm&\Leftrightarrow&3AB+4AB+3BC&=&216\;cm\\ \\&\Leftrightarrow&7AB+3BC&=&216\;cm\end{array}$
D'où, $\boxed{7AB+3BC=216\;cm}$
b) montrons que $3BC-5AB=0$
$ABC$ étant un triangle rectangle en $A$ alors, en appliquant le théorème de Pythagore, on obtient :
$$BC^{2}=AB^{2}+AC^{2}$$
Par suite, $BC=\sqrt{AB^{2}+AC^{2}}$
Mais, par hypothèse on a : $3AC=4AB$
Ce qui entraine : $AC=\dfrac{4}{3}AB$
Donc, en remplaçant on obtient :
$\begin{array}{rcl} BC&=&\sqrt{AB^{2}+\left(\dfrac{4}{3}AB\right)^{2}}\\ \\&=&\sqrt{AB^{2}+\dfrac{16}{9}AB^{2}}\\ \\&=&\sqrt{\dfrac{9+16}{9}AB^{2}}\\ \\&=&\sqrt{\dfrac{25}{9}AB^{2}}\\ \\&=&\dfrac{5}{3}AB\end{array}$
Ainsi, $BC=\dfrac{5}{3}AB\ \Rightarrow\ 3BC=5AB$
D'où, $\boxed{3BC-5AB=0}$
2) En utilisant les résultats de la question 1), calculons $AB\ $ et $\ BC$
D'après les résultats de la question 1), on obtient le système d'équations suivant :
$$\left\lbrace\begin{array}{rcl} 7AB+3BC&=&216\\3BC-5AB&=&0\end{array}\right.$$
On reconnait alors un système de deux équations à deux inconnues $AB\ $ et $\ BC.$
On peut donc procéder par addition pour déterminer les inconnues $AB\ $ et $\ BC.$
En multipliant la deuxième équation par $-1$, on a :
$$\left\lbrace\begin{array}{rcl} 7AB+3BC&=&216\\-3BC+5AB&=&0\end{array}\right.$$
Puis, en additionnant les deux équations, on obtient :
$\begin{array}{rcrcl} 7AB+3BC-3BC+5AB=216+0&\Rightarrow&12AB&=&216\\ \\&\Rightarrow&AB&=&\dfrac{216}{12}\\ \\&\Rightarrow&AB&=&18\end{array}$
D'où, $\boxed{AB=18\;cm}$
En reportant dans la deuxième équation, on obtient :
$\begin{array}{rcrcl} 3BC-5AB=0&\Rightarrow&BC&=&\dfrac{5}{3}AB\\ \\&\Rightarrow&BC&=&\dfrac{5\times 18}{3}\\ \\&\Rightarrow&BC&=&\dfrac{90}{3}\\ \\&\Rightarrow&BC&=&30\end{array}$
Ainsi, $\boxed{BC=30\;cm}$
Déduisons-en $AC.$
Comme $3AC=4AB$ alors, $AC=\dfrac{4}{3}AB$
Donc, $AC=\dfrac{4\times 18}{3}=\dfrac{72}{3}=24$
D'où, $\boxed{AC=24\;cm}$

Exercice 3
Un commerçant fixe le prix de vente de chacun de ses articles en prévoyant un bénéfice de $25$ pour cent.
Soit $x$ le prix d'achat d'un article et $p$ son prix de vente.
1) Justifions que :
$$p=\dfrac{5}{4}x$$
En effet, le commerçant prévoit un bénéfice de $25$ pour cent pour chaque article. Cela signifie que ce bénéfice représente $\dfrac{25}{100}$ du prix d'achat de l'article considéré.
Soit $x$ le prix d'achat d'un article et $B$ le bénéfice réalisé sur cet article.
Alors, on a : $B=\dfrac{25}{100}x$
Par suite,
$\begin{array}{rcl} p&=&x+B\\ \\&=&x+\dfrac{25}{100}x\\ \\&=&x+\dfrac{1\times 25}{4\times 25}x\\ \\&=&x+\dfrac{1}{4}x\\ \\&=&\dfrac{4}{4}x+\dfrac{1}{4}x\\ \\&=&\dfrac{5}{4}x\end{array}$
D'où, $\boxed{p=\dfrac{5}{4}x}$
2) Calculons le prix de vente d'un article acheté à $400\text{ F}.$
On a : $p=\dfrac{5}{4}x$ avec, $x=400\text{ F}.$
Donc,
$\begin{array}{rcl} p&=&\dfrac{5}{4}\times 400\\ \\&=&\dfrac{5\times 400}{4}\\ \\&=&500\end{array}$
Ainsi, $\boxed{p=500\text{ F}}$
3) Calculons le prix d'achat d'un article vendu à $1250\text{ F}.$
Comme $p=\dfrac{5}{4}x$ alors, $4p=5x$
Ce qui donne : $x=\dfrac{4}{5}p$
Donc, si $p=1250\text{ F}$ alors,
$\begin{array}{rcl} x&=&\dfrac{4}{5}\times 1250\\ \\&=&\dfrac{4\times 1250}{5}\\ \\&=&1000\end{array}$
D'où, $\boxed{x=1000\text{ F}}$
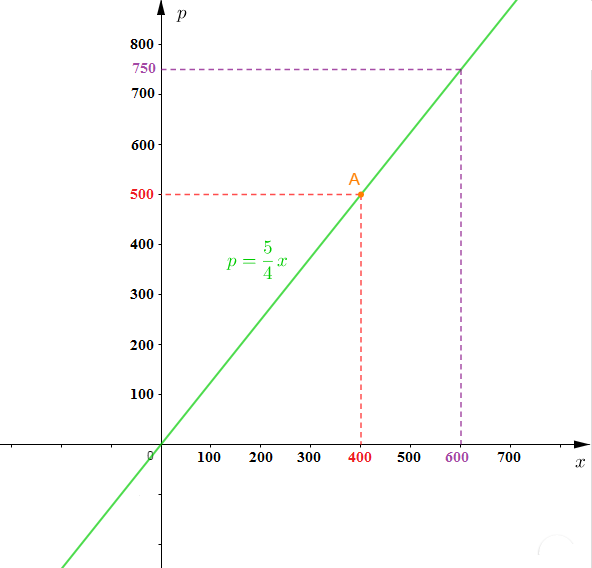
4) Représentons graphiquement dans un repère orthonormal $(O\;,\ \vec{i}\;,\ \vec{j})$, l'application qui à $x$ associe $p.$
Soit $p=\dfrac{5}{4}x$
$p$ est une application linéaire de coefficient linéaire $\dfrac{5}{4}.$
Donc, représenter $p$ revient à tracer la droite passant par $O$ origine du repère et par le point $A(400\;;\ 500)$

$$\text{Échelle :}\ 1\;cm\ \longrightarrow\ 100\text{ F}$$
5) Déterminons graphiquement le prix d'achat d'un article vendu à $750\text{ F}.$
Pour se faire, on projette cette valeur de $p$ sur la courbe parallèlement à l'axe des abscisses et à partir de la courbe on procède à une deuxième projection sur l'axe des abscisses parallèlement à l'axe des ordonnées.
Cela correspond alors à $600.$
Par conséquent, le prix d'achat d'un article vendu à $750\text{ F}$ est de $600\text{ F}.$
Exercice 4
On donne l'expression
$$A(x)=(2x+1)(5x+1)-(4x+2)(x-2)$$
1) Développons et réduisons $A(x).$
On a :
$\begin{array}{rcl} A(x)&=&(2x+1)(5x+1)-(4x+2)(x-2)\\ \\&=&(10x^{2}+2x+5x+1)-(4x^{2}-8x+2x-4)\\ \\&=&10x^{2}+7x+1-4x^{2}+6x+4\\ \\&=&10x^{2}-4x^{2}+7x+6x+1+4\\ \\&=&6x^{2}+13x+5\end{array}$
Ainsi, $\boxed{A(x)=6x^{2}+13x+5}$
2) Factorisons $A(x).$
On a :
$\begin{array}{rcl} A(x)&=&(2x+1)(5x+1)-(4x+2)(x-2)\\ \\&=&(2x+1)(5x+1)-2(2x+1)(x-2)\\ \\&=&(2x+1)[(5x+1)-2(x-2)]\\ \\&=&(2x+1)(5x+1-2x+4)\\ \\&=&(2x+1)(3x+5)\end{array}$
D'où, $\boxed{A(x)=(2x+1)(3x+5)}$
3) Résolvons dans $\mathbb{R}$ l'inéquation :
$$(2x+1)(3x+5)\leq 0$$
On a :
$2x+1=0\ \Leftrightarrow\ x=-\dfrac{1}{2}$
$3x+5=0\ \Leftrightarrow\ x=-\dfrac{5}{3}$
De plus :
$\begin{array}{rcrcl} 2x+1\geq 0&\Leftrightarrow&2x&\geq&-1\\ \\&\Leftrightarrow&x&\geq&-\dfrac{1}{2}\end{array}$
Donc, si $x\geq-\dfrac{1}{2}$ alors, $2x+1\geq 0$
et si $x\leq-\dfrac{1}{2}$ alors, $2x+1\leq 0$
De même,
$\begin{array}{rcrcl} 3x+5\geq 0&\Leftrightarrow&3x&\geq&-5\\ \\&\Leftrightarrow&x&\geq&-\dfrac{5}{3}\end{array}$
Ainsi, pour $x\geq-\dfrac{5}{3}$ on aura, $3x+5\geq 0$
et si $x\leq-\dfrac{5}{3}$ alors, $3x+5\leq 0$
Considérons le tableau de signes suivant :
$$\begin{array}{|c|lcccccr|}\hline x&-\infty&&-\tfrac{5}{3}&&-\tfrac{1}{2}&&+\infty\\ \hline 2x+1&&-&|&-&0&+&\\ \hline 3x+5&&-&0&+&|&+&\\ \hline (2x+1)(3x+5)&&+&0&-&0&+&\\ \hline\end{array}$$
On remarque que $(2x+1)(3x+5)\leq 0$ lorsque $x\in\left[-\dfrac{5}{3}\;;\ -\dfrac{1}{2}\right]$
D'où,
$$S=\left[-\dfrac{5}{3}\;;\ -\dfrac{1}{2}\right]$$
Auteur:
Diny Faye

Commentaires
Bassirou diaw (non vérifié)
sam, 08/15/2020 - 16:19
Permalien
Signaler une erreur
fdini
sam, 08/15/2020 - 17:35
Permalien
Merci Bassirou pour le retour
Merci Bassirou pour le retour
Cheikh (non vérifié)
dim, 08/30/2020 - 17:43
Permalien
Erreur
fdini
dim, 08/30/2020 - 19:00
Permalien
sur l'énoncé qu'on a c'est
sur l'énoncé qu'on a c'est bien $(2x+1)$
Anonyme (non vérifié)
lun, 07/10/2023 - 17:19
Permalien
AZERTY
Ajouter un commentaire