Corrigé Bac Maths S2 1er groupe 2014

1. Soit $z$ un nombre complexe non nul donné.

- L'écriture algébrique de $z$ est de la forme : $z=a+\mathrm{i}b$, avec $a$ sa partie réelle et $b$ sa partie imaginaire.

- L'écriture exponentielle de $z$ est de la forme : $z=r\mathrm{e}^{i\theta}$, avec $r$ son module et $\theta$ un de ses arguments.

- L'écriture trigonométrique de $z$ est de la forme : $z=r(\cos\theta+\mathrm{i}\sin\theta)$, avec $r$ son module et $\theta$ un de ses arguments.

 

2. Soient $K(z_{0})\;,\ M(z)$ et $M'(z')$ et soit $r$ la rotation de centre $K(z_{0})$ qui transforme $M(z)$ en $M'(z')$ on a : $$\left\{\begin{array}{lcl} KM' &=& KM \\ (\overrightarrow{KM},\ \overrightarrow{KM'}) &=& \theta\ [2\pi] \end{array}\right.\qquad (1)$$

Ce qui est équivalent à $$\left\{\begin{array}{lcl} |z'-z_{0}| &=& |z-z_{0}| \\ \\ arg\left(\dfrac{z'-z_{0}}{z-z_{0}}\right) &\equiv & \theta\ [2\pi] \end{array}\right.\qquad (2)$$

D'où $z'=\mathrm{e}^{\mathrm{i}\theta}z+z_{0}\left(1-\mathrm{e}^{\mathrm{i}\theta}\right)$

 

B) Soit $z_{0}=1-\mathrm{i}\sqrt{3}$

 

1. Écriture trigonométrique de $z_{0}$.

On a $|z_{0}|=\sqrt{1+3}=2$,

Soit $\theta$ un argument de $z_{0}$ alors $\cos\theta=\dfrac{1}{2}$ et $\sin\theta=-\dfrac{\sqrt{3}}{2}$ ce qui donne $\theta=-\dfrac{\pi}{3}\ [2\pi]$ d'où $$z_{0}=2\left(\cos\dfrac{\pi}{3}-\mathrm{i}\sin\dfrac{\pi}{3}\right)$$ 

 

2. Calculons $z_{0}^{4}$.

$z_{0}^{4}=\left[2\left(\cos\dfrac{\pi}{3}-\mathrm{i}\sin\dfrac{\pi}{3}\right)\right]^{4}=16\left(\cos\dfrac{4\pi}{3}-\mathrm{i}\sin\dfrac{4\pi}{3}\right)=16\left(-\dfrac{1}{2}+\mathrm{i}\dfrac{\sqrt{3}}{2}\right)$

 

D'où $$z_{0}^{4}=-8+\mathrm{i}8\sqrt{3}$$

 

3. Résolvons l'équation $z^{4}=1$

 

$z^{4}=1$ implique $|z|^{4}=1\ $ et $\ 4\;arg\;z=0\ [2\pi]$ ce qui donne $$|z|=1\quad\text{ et }\quad arg\;z=k\dfrac{\pi}{2}\;,\quad k\in\mathbb{Z}$$

d'où l'ensemble des solutions $S$ de l'équation $z^{4}=1$ est $$S=\{-1;\ 1;\ \mathrm{i};\ -\mathrm{i}\}$$

 

4. Déduisons-en les solutions de $(E)\ :\ z^{4}=-8+8\mathrm{i}\sqrt{3}.$

$z^{4}=-8+8\mathrm{i}\sqrt{3}$ est équivalent à $$\dfrac{z^{4}}{-8+8\mathrm{i}\sqrt{3}}=1$$

ce qui est équivalent, d'après B) 2), à $$\left(\dfrac{z}{1-\mathrm{i}\sqrt{3}}\right)^{4}=1$$

Ce qui donne d'après B) 3) les solutions suivantes :

- Sous forme algébrique : $$z_{0}=1-\mathrm{i}\sqrt{3}\;,\ z_{1}=-1+\mathrm{i}\sqrt{3}\;,\ z_{2}=\sqrt{3}+\mathrm{i}\;,\ z_{3}=-\sqrt{3}-\mathrm{i}$$

- Sous forme trigonométrique : $$z_{0}=2\left(\cos\dfrac{\pi}{3}-\mathrm{i}\sin\dfrac{\pi}{3}\right)\;,\ z_{1}=2\left(\cos\dfrac{2\pi}{3}+\mathrm{i}\sin\dfrac{2\pi}{3}\right)\;,\ z_{2}=2\left(\cos\dfrac{\pi}{6}+\mathrm{i}\sin\dfrac{\pi}{6}\right)\;,\ z_{3}=2\left(\cos\dfrac{7\pi}{6}+\mathrm{i}\sin\dfrac{7\pi}{6}\right)$$ 

 

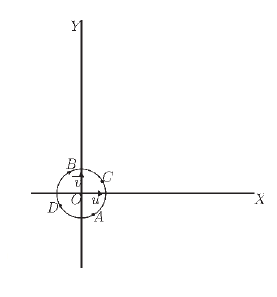
5. 

 

6. Soit $r$ la rotation de centre $O$ et d'angle $\dfrac{\pi}{2}$

D'après A) 2) si $M'(z')$ est l'image de $M(z)$ par $r$ alors $$z'=z\mathrm{e}^{\mathrm{i}\frac{\pi}{2}}$$

 

7. Soient les points $A\;,\ B\;,\ C$ et $D$ d'affixes respectives $z_{A}=z_{0}\;,\ z_{B}=z_{1}\;,\ z_{C}=z_{2}$ et $z_{D}=z_{3}.$

Vérifions que $r(A)=C$.

$$z_{A}\mathrm{e}^{\mathrm{i}\frac{\pi}{2}}=2\mathrm{e}^{-\mathrm{i}\frac{\pi}{3}}\mathrm{e}^{\mathrm{i}\frac{\pi}{2}}=2\mathrm{e}^{\mathrm{i}\frac{\pi}{6}}=z_{C}$$

d'où $r(A)=C$.

Vérifions que $r(C)=B$.

$$z_{C}\mathrm{e}^{\mathrm{i}\frac{\pi}{2}}=2\mathrm{e}^{\mathrm{i}\frac{\pi}{6}}\mathrm{e}^{\mathrm{i}\frac{\pi}{2}}=2\mathrm{e}^{\mathrm{i}\frac{4\pi}{6}}=2\mathrm{e}^{\mathrm{i}\frac{2\pi}{3}}=z_{B}$$

d'où $r(C)=B$.

Vérifions que $r(B)=D$.

$$z_{B}\mathrm{e}^{\mathrm{i}\frac{\pi}{2}}=2\mathrm{e}^{\mathrm{i}\frac{2\pi}{3}}\mathrm{e}^{\mathrm{i}\frac{\pi}{2}}=2\mathrm{e}^{\mathrm{i}\frac{7\pi}{6}}=z_{D}$$

d'où $r(B)=D$.

 

8. $r(A)=C$ implique $|z_{A}|=|z_{C}|$,

$r(C)=B$ implique $|z_{C}|=|z_{B}|$,

$r(B)=D$ implique $|z_{B}|=|z_{D}|$

D'où $$|z_{A}|=|z_{C}|=|z_{B}|=|z_{D}|=2$$

Ce qui est équivalent à $$OA=OB=OC=OD=2$$

D'où les points $A\;,\ B\;,\ C$ et $D$ sont situés sur le même cercle de centre $O$ et de rayon 2.

Une boîte contient 8 cubes indiscernables au toucher : $R_{1}\;,\ R_{2}\;,\ R_{2}\;,\ R_{2}\;,\ V_{1}\;,\ V_{1}\;,\ V_{2}\;,\ J_{2}.$

$R$ représente la couleur rouge, $V$ la couleur verte, $J$ la couleur jaune, 1 et 2

les numéros des couleurs.

A) Soit $(\Omega,\ \mathcal{P}(\Omega),\ p)$ un espace probabilisé. Soient $A$ et $B$ deux événements de cet espace probabilisé.

$A$ et $B$ sont indépendants si et seulement si $p(A\cap B)=p(A)\times p(B)$

 

B) On choisit successivement et sans remise 2 cubes de la boîte.

 

1. Soient les événements $A$ : "Obtenir des cubes de couleurs différentes" et

$B$ : "Obtenir au plus un cube portant le numéro 2"

 

a) $p(A)=\dfrac{A_{4}^{1}\times A_{4}^{1}+ A_{3}^{1}\times A_{5}^{1}+A_{1}^{1}\times A_{7}^{1}}{A_{8}^{2}}=\dfrac{19}{28}$

 

b) $p(\overline{B})=\dfrac{A_{5}^{2}}{A_{8}^{2}}=\dfrac{5}{14}$ d'où $p(B)=\dfrac{9}{14}$ 

 

c) Calculons $p(A\cap B)$ et comparons-le avec $p(A)\times p(B)$

$A\cap B$, l'événement : "Obtenir des cubes de couleurs différentes avec au plus un portant le numéro 2".

Les différentes possibilités sont :

$(R_{1}\;,\ V_{1})\;,\ (R_{1}\;,\ V_{1})\;,\ (V_{1}\;,\ R_{1})\;,\ (V_{1}\;,\ R_{1})$
$(R_{2}\;,\ V_{1})\;,\  (V_{1}\;,\ R_{2})\;,\  (R_{2}\;,\ V_{1})\;,\ (V_{1}\;,\ R_{2})\;,\ (R_{2}\;,\ V_{1})\;,\ (V_{1}\;,\ R_{2})$
$(R_{2}\;,\ V_{1})\;,\ (V_{1}\;,\ R_{2})\;,\ (R_{2}\;,\ V_{1})\;,\ (V_{1}\;,\ R_{2})\;,\  (R_{2}\;,\  V_{1})\;,\ (V_{1}\;,\ R_{2})\;,\ (R_{1}\;,\ J_{2})$
$(J_{2}\;,\ R_{1})\;,\ (V_{1}\;,\ J_{2})\;,\ (J_{2}\;,\ V_{1})\;,\ (V_{1}\;,\ J_{2})\;,\ (J_{2}\;,\ V_{1})\;,\ (R_{1}\;,\  V_{2})\;,\  (V_{2}\;,\ R_{1})$ 

 

Donc $p(A\cap B)=\dfrac{3}{7}$ 

 

Ou encore $p(A\cap B)=\dfrac{C_{2}^{1}\times A_{2}^{2}+ C_{3}^{1}\times C_{2}^{1}\times A_{2}^{2}+A_{2}^{2}+C_{2}^{1}\times A_{2}^{2}+A_{2}^{2}}{A_{8}^{2}}=\dfrac{3}{7}$

Or $p(A)\times p(B)=\dfrac{9}{14}\times\dfrac{19}{28}$ qui est différent de 3 d'où $A$ et $B$ ne sont pas indépendants.

 

2. Les valeurs prises par $X$ :

$X=\{0\;,\ 1\;,\ 2\}$

 

a) La loi de probabilité de $X$ :

$$\begin{array}{|c|c|c|c|} \hline X=a_{i} & 0 & 1 & 2   \\ \hline p(X=a_{i}) & \dfrac{3}{14} & \dfrac{4}{7} & \dfrac{3}{14} \\ \hline \end{array}$$

 

b) Espérance mathématique $E(X)$ de $X$ :

$E(X)=\sum_{j=1}^{m}x_{j}p(X=x_{j})$,

$E(X)=\dfrac{4}{7}+2\times\dfrac{3}{14}=1$ 

 

c) Variance V (X) de X :

$V(X)=\sum_{j=1}^{m}x_{j}^{2}p(X=x_{j})-(E(X))^{2}$,

$V(X)=\dfrac{4}{7}+4\times\dfrac{3}{14}-1=\dfrac{3}{7}$

 

C) Tirage simultané de 3 cubes de la boîte :

 

a) $p(C)=\dfrac{C_{3}^{3}\times C_{3}^{2}\times C_{5}^{1}}{C_{8}^{5}}=\dfrac{2}{7}$ 

 

b) $p_{n}=p(D_{n})=1-\left(\dfrac{5}{7}\right)^{n}$

 

c)  $(p_{n})_{n\in\mathbb{N}}$ est strictement croissante et $$\lim_{n\rightarrow +\infty}p_{n}=1$$

PARTIE A

1. a) $g(x)$ existe si $=\neq 1$ avec $x>0$

$$D_{g}=]0\;;\ 1[\cup]1\;;\ +\infty[$$

 

b) $\lim_{x\rightarrow 0^{+}}g(x)=0\;;\ \lim_{x\rightarrow +\infty}g(x)=-\infty$

 

$\lim_{x\rightarrow 1^{-}}g(x)=\lim_{x\rightarrow 1^{-}}\dfrac{x}{x-1}-\ln|x-1|=\lim_{x\rightarrow 1^{-}}\dfrac{x-(x-1)\ln(1-x)}{x-1}=-\infty$

 

$\lim_{x\rightarrow 1^{+}}g(x)=\lim_{x\rightarrow 1^{+}}\dfrac{x}{x-1}-\ln|x-1|=\lim_{x\rightarrow 1^{+}}\dfrac{x-(x-1)\ln(x-1)}{x-1}=+\infty$

 

2) $x\mapsto\ \dfrac{x}{x-1}$ et $x\mapsto\ \ln|x-1|$ sont dérivables pour tout $x\neq 1$ d'où $g$ est dérivable sur $D_{g}$ et $$g'(x)=\dfrac{-1}{(x-1)^{2}}-\dfrac{1}{x-1}=-\dfrac{x}{(x-1)^{2}}$$

 

Sur $D_{g}$,  $g'(x)<0$.

Tableau de variations de $g$ :

 

$$\begin{array}{|c|lcr||lcr|} \hline x  & 0 &  &  & 1 &  & +\infty \\ \hline g'(x) &  & - &  &  & - &    \\ \hline  & 0  &  &  & +\infty  &   &    \\ g &   &  \searrow &  &  & \searrow &   \\  &   &  & -\infty &  &  &  -\infty  \\ \hline \end{array}$$

 

3. Sur $]1\;;\ +\infty[$, $g$ est dérivable et strictement décroissante donc elle réalise

une bijection de $]1\;;\ +\infty[$ vers $]-\infty\;;\ +\infty[.$

Or $0\in\mathbb{R}$ il existe donc $\alpha\in\;]1\;;\ +\infty[$ tel que $g(\alpha)=0.$

Montrons que $4<\alpha<5$.

$g(4)\simeq 0.23$ et $g(5)\simeq -0.14$

$g(4)\times g(5)<0$ donc $4<\alpha<5$.

 

4. Sur $]1\;;\ \alpha[\ g(x)>0$ et sur $]\alpha\;;\ +\infty[\ g(x)<0$

 

PARTIE B

 

Soit

$$f(x)=\left\{\begin{array}{ll} \dfrac{\ln|x-1|}{x}\;,\quad \text{si }x>0 \\ \\ \dfrac{-6\mathrm{e}^{x}}{\mathrm{e}^{2x}+3\mathrm{e}^{x}+2}\;,\quad\text{si }x\leq 0 \end{array}\right.\qquad (3)$$

 

1. a) $x\mapsto\ \dfrac{\ln|x-1|}{x}$ est définie si $x\neq 0$ et $x\neq 1$,

d'où elle est définie sur $]0\;;\ 1[\cup]1\;;\ +\infty[.$

$\dfrac{-6\mathrm{e}^{x}}{\mathrm{e}^{2x}+3\mathrm{e}^{x}+2}$ est définie pour tout $x\in\mathbb{R}$, d'où elle est définie sur $]-\infty\;;\ 0].$

Donc $D_{f}=]-\infty\;;\ 0]\cup]0\;;\ 1[\cup]1\;;\ +\infty[=\mathbb{R}\setminus\{1\}$

 

$\lim_{x\rightarrow -\infty}f(x)=\lim_{x\rightarrow -\infty}\dfrac{-6\mathrm{e}^{x}}{\mathrm{e}^{2x}+3\mathrm{e}^{x}+2}=0\;;\ \lim_{x\rightarrow +\infty}f(x)=\lim_{x\rightarrow +\infty}\dfrac{\ln|x-1|}{x}=0$

 

$\lim_{x\rightarrow 1^{-}}f(x)=\lim_{x\rightarrow 1^{-}}\dfrac{\ln(1-x)}{x}=-\infty\;;\ \lim_{x\rightarrow 1^{+}}f(x)=\lim_{x\rightarrow 1^{+}}\dfrac{\ln(x-1)}{x}=-\infty$

 

b) La droite d'équation $x=1$ est une asymptote verticale à la courbe

$(\mathcal{C}_{f})$ de $f$ et la droite d'équation $y=0$ est une asymptote horizontale à la courbe $(\mathcal{C}_{f})$ de $f$ aux voisinages de $-\infty$ et $+\infty.$

 

2. a) $\lim_{x\rightarrow 0^{-}}f(x)=\lim_{x\rightarrow 0^{-}}\dfrac{-6\mathrm{e}^{x}}{\mathrm{e}^{2x}+3\mathrm{e}^{x}+2}=-1\;;\ \lim_{x\rightarrow 0^{+}}f(x)=\lim_{x\rightarrow 0^{+}}\dfrac{\ln(1-x)}{x}=-1$

 

on a aussi $f(0)=\dfrac{-6\mathrm{e}^{0}}{\mathrm{e}^{0}+3\mathrm{e}^{0}+2}=-1$

 

$\lim_{x\rightarrow 0^{-}}f(x)=\lim_{x\rightarrow 0^{+}}f(x)=f(0)$

 

Donc $f$ est continue en 0.

 

b) On admet que $\lim_{x\rightarrow 0^{+}}\dfrac{\ln(1-x)+x}{x^{2}}=\dfrac{-1}{2}$. 

 

Et on a $\lim_{x\rightarrow 0^{-}}\dfrac{f(x)-f(0)}{x-0}=\dfrac{\dfrac{-6\mathrm{e}^{x}}{\mathrm{e}^{2x}+3\mathrm{e}^{x}+2}+1}{x}=\lim_{x\rightarrow 0^{-}}\dfrac{\mathrm{e}^{2x}-3\mathrm{e}^{x}+2}{x(\mathrm{e}^{2x}+3\mathrm{e}^{x}+2)}=\lim_{x\rightarrow 0^{-}}\dfrac{\dfrac{\mathrm{e}^{2x}-3\mathrm{e}^{x}+2}{x}}{\mathrm{e}^{2x}+3\mathrm{e}^{x}+2}$

 

Or $\lim_{x\rightarrow 0^{-}}\dfrac{\mathrm{e}^{2x}-3\mathrm{e}^{x}+2}{x}=\mathrm{e}^{2\times 0}-3\mathrm{e}^{0}=-1$

 

d'où $\lim_{x\rightarrow 0^{-}}\dfrac{f(x)-f(0)}{x-0}=-\dfrac{1}{6}$.

 

$f'_{d}(0)=-\dfrac{1}{2}$ et $f'_{g}(0)=-\dfrac{1}{6}\;,\ f'_{d}(0)\neq f'_{g}(0)$ d'où $(\mathcal{C}_{f})$ admet deux demi-tangentes au point d'abscisse 0.

 

3. a) $f(\alpha)=\dfrac{\ln(\alpha-1)}{\alpha}$ or $g(\alpha)=0$ nous donne $\dfrac{\alpha}{\alpha-1}=\ln(\alpha-1)$ d'où $f(\alpha)=\dfrac{\alpha}{\alpha-1}\times\dfrac{1}{\alpha}=\dfrac{1}{\alpha-1}$.

 

b) Sur $]0\;;\ 1[\cup]1\;;\ +\infty[\;,\ f'(x)=\dfrac{\dfrac{1}{x-1}x-\ln|x-1|}{x^{2}}=\dfrac{\dfrac{x}{x-1}-\ln|x-1|}{x^{2}}=\dfrac{g(x)}{x^{2}}$

 

Sur $]-\infty\;;\ 0[\;,\ f'(x)=\dfrac{-6\mathrm{e}^{x}(3\mathrm{e}^{2x}+6\mathrm{e}^{x}+2)}{(\mathrm{e}^{2x}+3\mathrm{e}^{x}+2)^{2}}$

 

Sur $]0\;;\ 1[\cup]1\;;\ +\infty[\;,\ f'(x)$ a le même signe que $g(x)$, 

 

Sur $]-\infty\;;\ 0[\;,\ f'(x)<0$.

 

Dressons le tableau de variations de la fonction $f$.

 

$$\begin{array}{|c|lcrlcr||lcccr|} \hline x  & -\infty &  &  & 0 &  &  & 1 & & \alpha &  & +\infty \\ \hline f'(x) &  & - & -\frac{1}{6} & ||-\frac{1}{2} & - &  &  & + & 0 & - &  \\ \hline  & 0 &  &  &  &  &  &  &  & \frac{1}{\alpha-1} &   &    \\ f(x) &   &  \searrow &  &  &  &   \\  &  &   &  & -1 &  &  &  & \nearrow &  & \searrow &  \\   &  &  &  &  & \searrow &  &  &  &  &  &  \\  &  &  &  &  &  & -\infty & -\infty &  &  &  & 0  \\ \hline \end{array}$$

 

4. Traçons la courbe $(\mathcal{C}_{f})$ de $f$ dans un repère orthonormé $(0;\ \vec{i},\ \vec{j})$ d'unité graphique $2\;cm.$

 

 

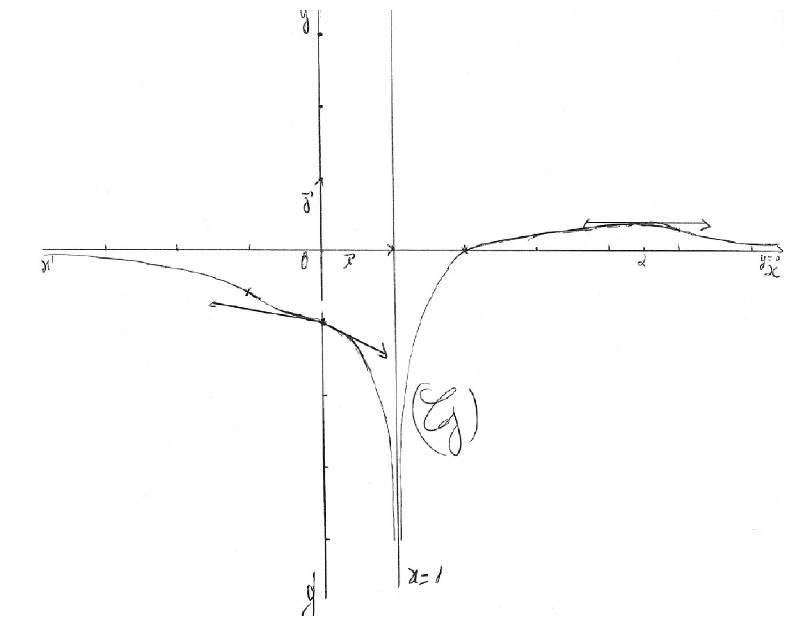
5. a) $\dfrac{-6x}{x^{2}+3x+2}=\dfrac{a}{x+2}+\dfrac{b}{x+1}$ nous donne $a=-12$ et $b=6$, 

d'où $\dfrac{-6x}{x^{2}+3x+2}=\dfrac{-12}{x+2}+\dfrac{6}{x+1}$.

 

b) D'après a) $\dfrac{-6\mathrm{e}^{x}}{\mathrm{e}^{2x}+3\mathrm{e}^{x}+2}=\dfrac{-12}{\mathrm{e}^{x}+2}+\dfrac{6}{\mathrm{e}^{x}+1}=\dfrac{-12}{\mathrm{e}^{x}(1+2\mathrm{e}^{-x})}+\dfrac{6}{\mathrm{e}^{x}(1+\mathrm{e}^{-x})}$

 

D'où $\dfrac{-6\mathrm{e}^{x}}{\mathrm{e}^{2x}+3\mathrm{e}^{x}+2}=\dfrac{-12\mathrm{e}^{-x}}{1+2\mathrm{e}^{-x}}+\dfrac{6\mathrm{e}^{-x}}{1+\mathrm{e}^{-x}}$

 

c) Soit $\mathcal{A}$ l'aire du domaine délimité par l'axe des abscisses, la courbe,

les droites d'équations $x=-\ln 2$ et $x=0.$

$\mathcal{A}=\int_{-\ln 2}^{0}-f(x)\mathrm{d}x\times u.a=\int_{-\ln 2}^{0}-\dfrac{-6\mathrm{e}^{x}}{\mathrm{e}^{2x}+3\mathrm{e}^{x}+2}\mathrm{d}x\times u.a$

 

$=\int_{-\ln 2}^{0}\dfrac{12\mathrm{e}^{-x}}{1+2\mathrm{e}^{-x}}-\dfrac{6\mathrm{e}^{-x}}{1+\mathrm{e}^{-x}}\mathrm{d}x=[-6\ln(1+2\mathrm{e}^{-x})+6\ln(1+\mathrm{e}^{-x})]_{-\ln 2}^{0}\times 4\;cm^{2}$

 

d'où $\mathcal{A}=24\ln\dfrac{10}{9}\;cm^{2}$