Série d'exercices : Oscillations mécaniques libres - Ts
Classe:
Terminale
Exercice 1
Pendule élastique horizontal
On considère un ressort dont une extrémité est fixe et dont l'autre est reliée à un corps $M$ qui peut glisser sans frottement sur un plan horizontal (figure 1).
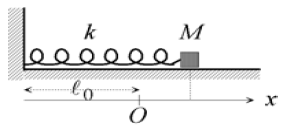
Le corps $M$ est assimilé à une masse ponctuelle $m.$
Le ressort, de raideur $k$ et de masse négligeable, a une longueur au repos $\ell_{0}.$
1) Établir l'équation différentielle du mouvement du corps $M.$
On utilisera un axe $Ox$ dont l'origine $O$ correspond à la position de $M$ lorsque le ressort est au repos.
2) On considère les conditions initiales de mouvement suivantes :
a) $t=0$ le corps $M$ est en $x=x_{0}>0$ et la vitesse initiale de $M$ est nulle.
b) $t=0$ le corps $M$ est en $x=x_{0}$ et la vitesse de $M$ est $\overrightarrow{v_{0}}=v_{0}\overrightarrow{\mathrm{e_{x}}}$ avec $v_{0}>0.$
Déterminer l'équation horaire du mouvement du corps $M$ dans les cas a) et b).
Pendule élastique vertical
Un ressort identique à celui du 1) est lié à un corps $M$, supposé ponctuel et de masse $m$, qui peut se déplacer verticalement dans le champ de pesanteur terrestre.
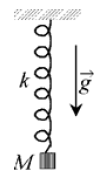
1) Déterminer la position d'équilibre du corps $M.$
2) Établir l'équation différentielle du mouvement de $M.$
Exercice 2
Oscillations d'un pendule simple
Un pendule simple est constitué d'une masse $m$ suspendue à un fil non élastique, de masse négligeable, de longueur $\ell.$
Il est écarté de sa position d'équilibre d'un angle $\theta_{0}$ et lâché sans vitesse initiale.
On note $\theta$ l'angle que fait à l'instant $t$ la direction du pendule $OM$ avec l'axe $Ox$ (voir schéma).
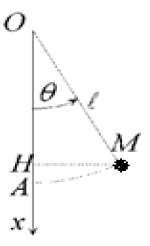
1) Conservation de l'énergie
a) Donner l'expression de l'énergie cinétique $E_{c}(\dot{\theta})$, de l'énergie potentielle de pesanteur $E_{p}(\theta)$ et celle de l'énergie totale $E$ en tenant compte des conditions initiales.
On prendra la référence de l'énergie potentielle à la position d'équilibre.
b) Établir l'équation différentielle du mouvement.
2) Petites oscillations
Dans tout ce qui suit, on se place dans le cas de petites oscillations : $\theta_{0}$ est suffisamment petit pour que l'on puisse poser $\sin\theta\approx\theta$ et $\cos\theta\approx 1-\dfrac{\theta^{2}}{2}.$
a) Résoudre l'équation différentielle vérifiée par $\theta(t)$ en tenant compte des conditions initiales.
Quelle est la période des oscillations du pendule ?
b) Donner l'expression de l'énergie cinétique $E_{c}(t)$ et de l'énergie potentielle $E_{p}(t)$ en fonction du temps et vérifier la conservation de l'énergie.
Montrer qu'en valeur moyenne dans le temps on a équipartition de l'énergie : $(E_{c})=(E_{p}).$
3) Amortissement du pendule
On tient compte maintenant de la viscosité de l'air qui est responsable d'une force de frottement de sens opposé à la vitesse : $\overrightarrow{F}=f\overrightarrow{v}$ où le nombre positif $f$ est le coefficient de frottement visqueux.
a) Donner la projection de l'équation fondamentale de la dynamique sur la base orthonormale $\overrightarrow{e_{r}}$ et $\overrightarrow{e_{\theta}}$ des coordonnées polaires du point $M$ (voir schéma) et en déduire l'équation différentielle du mouvement.
Montrer que l'équation vérifiée par $\theta$ pour des mouvements de faible amplitude est de la forme :
$$\ddot{\theta}+\dfrac{\omega_{0}}{Q}\dot{\theta}+\omega_{0}^{2}\theta=0$$
où $Q$ est un nombre sans dimension appelé facteur de qualité de l'oscillateur et $\omega_{0}$ est la pulsation des oscillations non amorties.
b) Montrer que la solution de cette équation différentielle, avec les mêmes conditions initiales peut traduire différents comportements du pendule suivant la valeur du coefficient de frottement $f$ ; on examinera les cas suivants et on tracera le graphe de $\theta(t)$ :
$(i)\qquad\qquad Q>\dfrac{1}{2}\qquad (amortissement\ faible\ : \ régime\ oscillatoire)$
$(ii)\qquad\qquad Q<\dfrac{1}{2}\qquad (amortissement\ fort\ :\ régime\ hypercritique)$
$(iii)\qquad\qquad Q=\dfrac{1}{2}\qquad (régime\ critique)$
c) Bilan énergétique
Utiliser le théorème de l'énergie cinétique entre deux instants voisins $t$ et $t+\mathrm{d}t$ pour montrer que l'énergie du système $E=E_{c}+E_{p}$ diminue au cours du temps et interpréter ce résultat.
Exercice 3

Un solide, de masse $m=400g$, glisse sans frottements sur une table à coussin d'air horizontale.
Il est relié d'un côté à un ressort $R_{1}$ dont l'extrémité $A_{1}$ est fixe et de l'autre côté à $R_{2}$ dont l'extrémité $A_{2}$ est fixe.
Le ressort $R_{1}$, à l'équilibre, est allongé de $10\,cm$, $R_{2}$ est allongé de $8\,cm.$
1) Quelle est la constante de raideur $k_{2}$ de $R_{2}$, sachant que celle de $R_{1}$, $k_{1}$, est $40\,N\cdot m^{-1}.$
Le solide accomplit des oscillations de translation, parallèlement à $A_{1}A_{2}.$
2) a) Montrer que l'oscillateur est harmonique.
b) Calculer sa pulsation propre.
Le solide est écarté de $2\,cm$ de sa position d'équilibre, vers $A_{2}.$
De là, à $t=0$, on le lance vers $A_{1}$ à la vitesse de $0.1\,m\cdot s^{-1}.$
3) Quelle est la loi horaire du mouvement ?
L'état de référence pour l'énergie potentielle des deux ressorts est la position d'équilibre.
L'oscillateur est excité.
4) Calculer son énergie mécanique.
Exercice 4
Une tige homogène $OA$ de longueur $\ell=1m$, de masse $m=100\,g$ et de moment d'inertie par rapport à $\Delta$ $J=\dfrac{1}{3}m\cdot\ell^{2}$ peut osciller autour d'un axe horizontal $\Delta$, passant par son extrémité supérieure $O.$
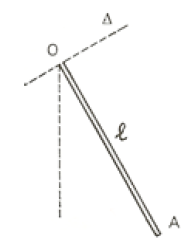
1) Montrer que, si les l'amplitude des oscillations est suffisamment faible, ces dernières sont forcément harmoniques.
2) Déterminer la pulsation propre de cet oscillateur.
A l'extrémité de la tige, en $A$, on fixe une masse pratiquement ponctuelle, $m'.$
La période des oscillations de faible amplitude est $T'=1.83s.$
3) Déterminer $m'.$
On retire la masse $m'.$
La tige est soudée en $O$ à un fil de torsion $OO'$, colinéaire à $\Delta$, l'axe de rotation horizontal de la barre.
Le fil $OO'$ a pour constante de torsion $C=0.2\,N\cdot m\cdot rad^{-1}$, il n'est pas tordu lorsque $OA$ est verticale.
4) a) Montrer que cet oscillateur n'est pas harmonique, mais qu'il peut être linéarisé.
b) Calculer dans ce cas sa pulsation propre.
Exercice 5 : Pendule et ressort
On considère une masse ponctuelle accrochée à l'extrémité d'un ressort de longueur $l$ dont le point de suspension est fixé en $O$, Cette masse $m$ est de plus accrochée à l'extrémité d'un ressort de raideur $k$ dont l'autre extrémité au point $A.$
A l'équilibre le ressort est horizontal et la masse est située en $O$ à la verticale du point de suspension du pendule (voir figure)
On supposera que le mouvement du pendule a lieu dans un plan (SCHEMA)
1 a) Établir l'équation différentielle qui régit le mouvement de la masse ponctuelle dans l'approximation des petits angles
b) En déduire les expressions de la période de la période et de la pulsation propre
2 a) Exprimer l'énergie potentielle du pendule supposé seul en fonction de l'angle $\theta$
On prendra l'origine de l'énergie potentielle à l'équilibre
b) Exprimer l'énergie potentielle du ressort supposé seul lorsqu'on écarte de l'angle $\theta$
c) Sachant que l'énergie potentielle totale est la somme de deux termes calculés précédemment ; déduire son expression dans l'approximation des petits angles $(\cos\theta\approx 1-\theta^{2}/2\;,\ \sin\theta\approx\theta)$
d) Exprimer l'énergie cinétique du pendule en fonction de l'angle $\theta.$
En déduire une expression de l'énergie totale du système dans l'approximation des petits angles
e) En déduire l'équation différentielle du mouvement.
Déterminer la pulsation du mouvement de la masse $m$ dans l'approximation des petits angles.
Exercice 6
Un solide $(S)$ de masse $m$ est attaché à l'une des extrémités d'un ressort horizontal parfaitement élastique, de constante de raideur $k$ et de masse négligeable devant celle du solide $(S).$
L'autre extrémité du ressort est fixe.
On écarte le solide $(S)$ de sa position d'équilibre de $x_{0}$ à un instant qu'on prend comme origine des dates, puis on l'abandonne sans vitesse.
On néglige les frottements et on étudie le mouvement du solide $(S)$ relativement à un repère galiléen $(O\;,\ \vec{i})$ d'origine $O$, la position du centre d'inertie de $(S)$ à l'équilibre et d'axe $ox$ horizontal (figure 1).
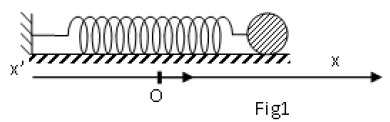
1) a) A une date $t$ quelconque, le centre d'inertie $G$ de $(S)$ a une élongation $x$ et sa vitesse instantanée est $v.$
Établir l'expression de l'énergie mécanique $E$ du système $\{$solide $(S)$, ressort$\}$ en fonction de $x$, $v$, $k$ et $m.$
b) Montrer que cette énergie mécanique $E$ est constante.
Exprimer sa valeur en fonction de $k$ et $x_{0}.$
c) En déduire que le mouvement de $(S)$ est rectiligne sinusoïdal
2) A l'aide d'un dispositif approprié, on mesure la vitesse instantanée $v$ du solide $(S)$ pour différentes élongations $x$ du centre d'inertie $G$ de $(S).$
Les résultats des mesures ont permis de tracer la courbe $v^{2}=f(x^{2})$ (figure 2)
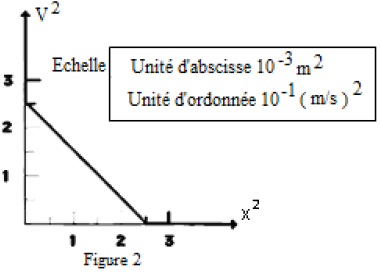
a) Justifier théoriquement l'allure de la courbe en établissant l'expression de $v^{2}.$
b) En déduire les valeurs de :
$-\ $ la pulsation $\omega_{0}$ et l'amplitude $x_{0}$ du mouvement de $(S)$,
c) Établir l'équation horaire du mouvement.
d) Sachant que l'énergie mécanique $E$ du système est égale à $0.0625\,J$, calculer les valeurs de la constante de raideur $k$ du ressort et la masse $m$ du solide
Exercice 7
Partie A :
Un pendule élastique horizontal est constitué par un solide $(S)$ de masse $m=500\,g$, attaché à l'une des extrémités d'un ressort horizontal, parfaitement élastique, de raideur $K$ et de masse négligeable par rapport à celle du solide, l'autre extrémité du ressort étant fixe (figure 1).
On néglige tout type de frottement et on étudie le mouvement du solide $(S)$ relativement à un repère galiléen $(O\;,\ \vec{i})$ horizontal, d'origine $O$ coïncidant avec la position d'équilibre du centre d'inertie du solide.
On écarte le solide $(S)$ de sa position d'équilibre d'une distance $X_{m}$ puis on le lâche sans vitesse.
Lorsque le solide passe par sa position d'abscisse $x_{0}$ $(x_{0}\neq 0)$ avec une vitesse initiale $v_{0}$ $(v_{0}\neq 0)$ en se dirigeant dans le sens positif, on déclenche le chronomètre $($c'est l'instant $t=0s)$ pour commencer l'étude du mouvement.
1) a) En appliquant la relation fondamentale de la dynamique au solide $(S)$, établir l'équation différentielle de son mouvement.
Quelle est la nature de ce mouvement ?
b) Montrer que $x(t)=X_{m}\sin(\omega_{0}t+\varphi_{x})$ est une solution de l'équation différentielle précédente à condition que la pulsation $\omega_{0}$ vérifie une expression qu'on donnera en fonction de $K$ et $m.$
Donner l'expression de la période propre $T_{0}$ des oscillations du solide $(S).$
c) Déduire l'expression de la vitesse du solide en fonction de $X_{m}$, $\omega_{0}$, $t$ et $\varphi_{x}.$
2) Montrer que $x_{0}$ et $v_{0}$ vérifient la relation $x_{02}+\dfrac{v_{0}^{2}}{\omega_{0}^{2}}=X_{m}^{2}$
3) Un ordinateur muni d'une interface et d'un capteur a enregistré les variations de l'énergie cinétique du solide $(S)$ au cours du temps $t$, le graphe obtenu sur l'écran de l'ordinateur est donné par la figure 2.
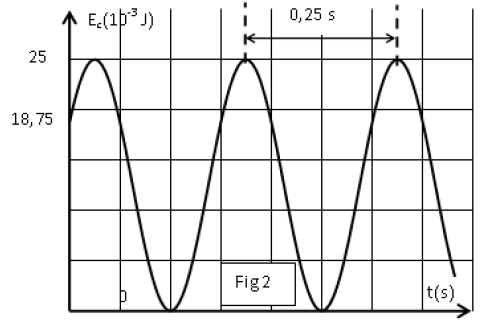
a) Donner l'expression de l'énergie mécanique $E$ du système $S_{0}=\{(S)+\text{ressort}\}$ en fonction de $x$, $v$, $K$ et $m$ avec $x$ élongation du solide $(S)$ et $v$ sa vitesse à un instant $t$ quelconque.
Montrer que l'énergie $E$ est constante puis donner son expression en fonction de $m$ et $V_{m}$ ; $V_{m}$ amplitude de la vitesse $v$ du solide.
Établir l'expression de l'énergie cinétique du solide $(S)$ en fonction $m$, $V_{m}$, $\omega_{0}$, $t$ et $\varphi.$
Montrer qu'on peut l'écrire sous la forme : $$E_{c}=\dfrac{E_{c\,max}}{2}(1+\cos(2\omega_{0}t+2\varphi_{x}))$$
b) En utilisant le graphe, trouver :
$-\ $ L'amplitude de la vitesse $V_{m}.$
$-\ $ La période propre $T_{0}.$
En déduire $X_{m}.$
$-\ $ La phase initiale $\varphi_{x}$ de l'élongation $x(t).$
c) Écrire la loi horaire du mouvement.
d) Calculer l'abscisse initiale $x_{0}(x(t=0))$ du solide $(S)$ dans le repère $(O\;,\ \vec{i})$, déduire sa vitesse initiale $v_{0}.$
Dans quel sens débute le mouvement du solide $(S)$ ?
e) Calculer la raideur $K$ du ressort.
Partie B :
Dans cette partie, le solide $(S)$ est soumis à une force de frottement visqueux $f=-h\overrightarrow{v}$ ou $h$ est une constante positive $h$ $(h=0.2$ u.s.i$).$
1) Donner le nom et l'unité de $h.$
2) Établir l'équation différentielle du mouvement du solide $(S)$ régissant les variations de son élongation $x(t).$
3) Montrer que l'énergie totale du système $S_{0}=\{(S)+\text{ressort}\}$ diminue au cours du temps.
4) À l'aide d'un dispositif approprié, on a enregistré les variations de la vitesse du solide en fonction du temps ; on a trouvé le graphe de la figure 3 :
Calculer l'énergie dissipée par la force de frottement entre les instants $t_{1}$ et $t_{2}.$
Exercice 8
Un pendule élastique est constitué d'un ressort à spires non jointives, de masse négligeable et de constante de raideur $K$, et d'un solide $(S)$ supposé ponctuel de masse $m.$
Le solide $(S)$ peut se déplacer sans frottement sur un plan horizontal.
Sa position est repérée par son abscisse $x$ dans le repère $(O\;,\ \vec{i})$ avec $O$ la position d'équilibre de $(S)$ (figure 1).
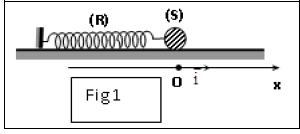
On soumet $(S)$ à une force excitatrice $\overrightarrow{F}=\overrightarrow{F}\cdot\vec{i}=F_{m}\sin(\omega\,t+\varphi_{F})\vec{i}$ et à une force de frottement $\overrightarrow{f}=-h\overrightarrow{v}$ avec $\overrightarrow{v}$ la vitesse de $(S)$ et $h$ une constante positive.
1) Établir l'équation différentielle régissant les variations de l'élongation $x.$
Pour une certaine valeur $h_{1}$ de $h$ et une valeur $\omega_{1}$ de $\omega$, on obtient les courbes de variations de $F$ et de $x$ en fonction de temps (figure 2).
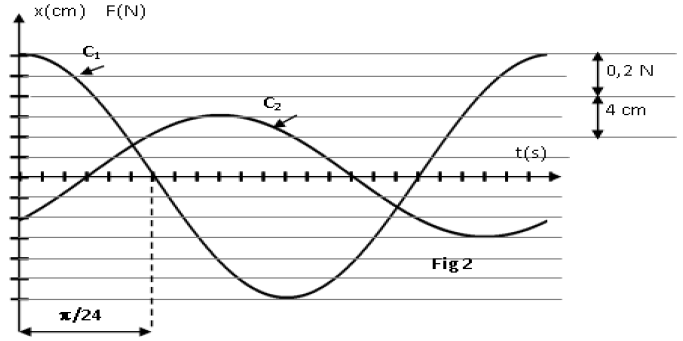
a) Montrer que la courbe $\mathcal{C_{1}}$ correspond à $F(t).$
b) Déterminer la valeur de $\omega_{1}$, $F_{m}$, $X_{m}$, et $\varphi_{F}-\varphi_{x}.$
c) Quelle est la valeur de $\varphi_{F}$ ?
Déduire celle de $\varphi_{x}.$
d) Faire la construction de Fresnel correspondante.
Déduire les expressions de $X_{m}$ et de $\sin(\varphi_{F}-\varphi_{x}).$
Calculer $h_{1}.$
Pour une certaine valeur $\omega_{r}$ de $\omega$, on constate que $X_{m}$ prend sa valeur la plus élevée.
a) Dans quel état se trouve l'oscillateur ?
b) On donne la courbe de variation de $\omega_{r}^{2}$ en fonction de $h^{2}$ (figure 3) ainsi que l'expression de $\omega_{r}=\sqrt{-\dfrac{h^{2}}{2m^{2}}+\dfrac{K}{m}}.$
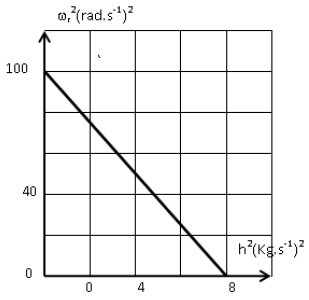
Déterminer $K$ et $m.$
2) En précisant l'analogie utilisée donner :
a) Le schéma du montage du circuit électrique analogue à l'oscillateur mécanique précédent.
b) L'expression de la charge maximale $Q_{m}$ du condensateur.
c) L'expression de la pulsation $\omega_{r}$ correspondant à la valeur la plus élevée de $Q_{m}.$
Exercice 9
Un solide $(C)$ supposé ponctuel de masse $m$ est accroché libre d'un ressort de masse négligeable et de constante de raideur $K$
On écarte verticalement $(C)$ d'une distance $a$ par rapport à sa position d'équilibre et on l'abandonne à lui-même sans vitesse à l'instant $t=0s$
La position de $(C)$ est repérée par rapport à sa position d'équilibre ; à l'instant $t$ par l'abscisse $x$ (figure 1)
1) Montrer que l'énergie potentielle du système $S$ $(C$, Terre ; ressort$)$ à l'instant sous la forme $E_{p}=\dfrac{1}{2}\left(x^{2}+\Delta\,l_{0}^{2}\right)$ avec $\Delta\,l_{0}$ étant l'allongement du ressort à l'équilibre
2) On donne la représentation graphique $E_{p}=f(x^{2})$ ( figure 2)
a) Déterminer graphiquement $a$, $k$, $\Delta\,l_{0}$
b) En déduire $m$
3) a) Montrer que le système est conservatif.
b) Exprimer l'énergie mécanique du système $(S)$ en fonction de ; $a$ et $k.$
c) En déduire l'énergie cinétique de $(S)$ à l'instant $t$ en fonction $k$, $a$ et $x.$
Exercice 10
Une masse $m$ est susceptible de se déplacer sans frottements sur un axe horizontal.
Elle est soumise à l'action de $2$ ressorts de même longueur à vide $l_{0}=20cm$ et de constantes de raideur différentes $k_{1}$ et $k_{2}.$
On donne :
$m=4kg$ ; $k_{1}=100N\cdot m^{-1}$ ; $k_{2}=300N\cdot m{-1}$ et $d=60cm.$
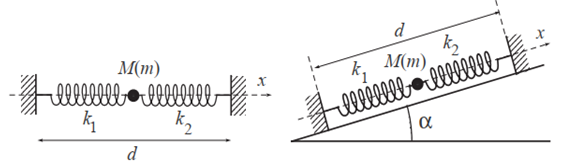
1. Déterminer les longueurs $l_{1}$ et $l_{2}$ des $2$ ressorts à l'équilibre.
2. On écarte la masse $m$ d'une distance $x$ à partir de sa position d'équilibre.
Déterminer l'équation différentielle du mouvement en prenant la position d'équilibre comme origine des abscisses.
2.1 Calculer la période et la fréquence des oscillations.
2.2 Donner l'expression de l'énergie mécanique de la masse.
On prendra la position d'équilibre comme état de référence pour l'énergie potentielle de pesanteur et la position du ressort à vide pour l'énergie potentielle élastique
2.3 Retrouver l'équation différentielle en utilisant la conservation de l'énergie mécanique
3. Les ressorts sont tendus le long d'un plan incliné de $\alpha=30^{\circ}$ avec l'horizontale
Mêmes questions.
Exercice 11
Un solide $(S)$ de masse $m$ est attaché à l'une des extrémités d'un ressort horizontal parfaitement élastique, de constante de raideur $k$ et de masse négligeable devant celle du solide $(S).$
L'autre extrémité du ressort est fixe.
On écarte le solide $(S)$ de sa position d'équilibre de $x_{0}$ à un instant qu'on prend comme origine des dates, puis on l'abandonne sans vitesse.
On néglige les frottements et on étudie le mouvement du solide $(S)$ relativement à un repère galiléen $(O\;,\ \vec{i})$ d'origine $O$, la position du centre d'inertie de $(S)$ à l'équilibre et d'axe $ox$ horizontal (fig. 1).
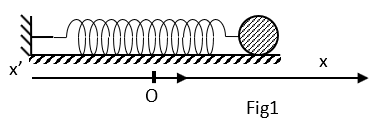
1) a) A une date $t$ quelconque, le centre d'inertie $G$ de $(S)$ a une élongation $x$ et sa vitesse instantanée est $v.$
Établir l'expression de l'énergie mécanique $E$ du système $\{\text{solide (S), ressort}\}$ en fonction de $x$, $v$, $k$ et $m.$
b) Montrer que cette énergie mécanique $E$ est constante.
Exprimer sa valeur en fonction de $k$ et $x_{0}.$
c) En déduire que le mouvement de $(S)$ est rectiligne sinusoïdal.
2) A l'aide d'un dispositif approprié, on mesure la vitesse instantanée $v$ du solide $(S)$ pour différentes élongations $x$ du centre d'inertie $G$ de $(S).$
Les résultats des mesures ont permis de tracer la courbe $v^{2}=f(x^{2})$ (fig. 2).
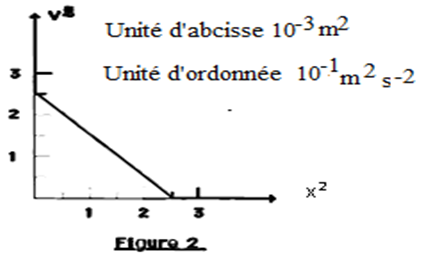
a) Justifier théoriquement l'allure de la courbe en établissant l'expression de$v^{2}.$
b) En déduire les valeurs de la pulsation $\omega_{0}$ et l'amplitude $x_{0}$ du mouvement de $(S)$
c) Établir l'équation horaire du mouvement.
d) Sachant que l'énergie mécanique $E$ du système est égale à $0.0625J$, calculer les valeurs de la constante de raideur $k$ du ressort et la masse $m$ du solide
Exercice 12
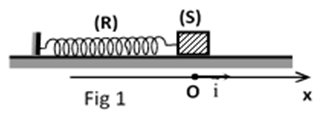
Le pendule élastique horizontal de la figure 1 est constitué par un solide $(S)$ de masse $m=0.2Kg$ soudé à l'une des extrémités d'un ressort $(R)$ à spires non jointives de masse négligeable et de constante de raideur $K$, l'autre extrémité est attaché à un support fixe.
A l'équilibre, le centre d'inertie $(G)$ du solide $(S)$ coïncide avec l'origine $O$ d'un repère espace horizontal $(O\;,\ \vec{i}).$
Partie A
A partir du point $O$, on écarte le solide $(S)$ vers un point $A$ d'abscisse $x_{A}$ et à la date $t=0s$, on l'abandonne à lui-même sans vitesse initiale.
Au cours de son mouvement, le solide $(S)$ se déplace sans frottement et son centre d'inertie $(G)$ est repéré par l'élongation $OG=x(t).$
Un système d'acquisition de données, enregistre les variations de l'élongation $x$ au cours du temps (Voir figure 2).
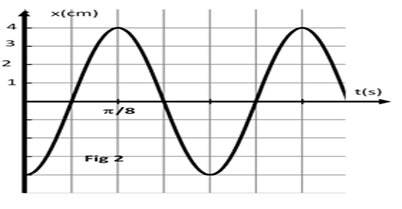
1) En utilisant le graphe
a) Préciser la nature de mouvement de $(S).$
b) Déterminer l'abscisse initiale $x_{A}$ du solide $(S)$ et la constante de raideur $K$ du ressort.
c) Dans quel sens, débute le mouvement du solide $(S).$
2) Écrire la loi horaire $x=f(t)$ de mouvement du solide.
Déduire l'équation différentielle du mouvement.
3) L'énergie cinétique du solide $E_{c}=\dfrac{mv^{2}}{2}$ varie au cours du temps selon une fonction sinusoïdale de période $T$
a) Établir l'expression de $E_{C}$ en fonction du temps.
b) Donner la valeur de $T.$
4) L'énergie mécanique du système $=\{\text{solide + ressort}\}$ est $E=E_{c}+E_{p}$ avec $E_{p}=\dfrac{Kx^{2}}{2}.$
a) Montrer que cette énergie est constante.
b) Comment apparaît cette énergie aux instants $t_{1}=0s$, $t_{2}=\dfrac{\pi}{16}s\ $ et $\ t_{3}=\dfrac{\pi}{8}s.$
Partie B
L'oscillateur est maintenant soumis à des forces de frottements visqueux équivalents à une force unique $\overrightarrow{f}=-h\overrightarrow{V}.$
Avec $h$ est une constante positive.
1) Établir l'équation différentielle vérifiée par l'élongation $x$ de $(G).$
2) Montrer que l'énergie totale du système $=\{\text{solide + ressort}\}$ diminue au cours du temps.
3) A l'aide d'un dispositif approprié, on a enregistré le diagramme d'espace de mouvement du solide, le résultat est donné par le graphe de la figure 3.
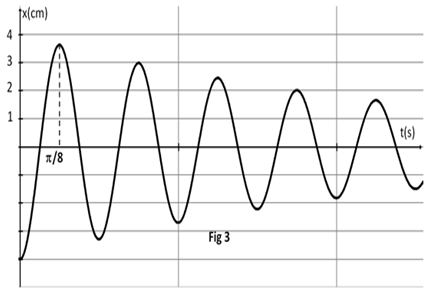
a) Quel est le nom du régime d'oscillations ?
b) Sachant que la variation de l'énergie totale du système $\{\text{solide + ressort}\}$ est égal au travail de la force de frottement.
Calculer ce travail entre les instants $t_{1}=0s$ et $t_{2}=\dfrac{7\pi}{8}$
Exercice 13
Un ressort à spire non jointives, de constante de raideur $K$, de masse négligeable, est posé sur un plan horizontal.
L'une des extrémités du ressort est fixe, l'autre est attachée à un solide $(S)$ de masse $m.$
Au cours de son mouvement, le solide $(S)$ est soumis à une force de frottement de la forme $\overrightarrow{f}=-h\overrightarrow{v}=(h$ : est une constante positive de valeur $h=0.1$ U.S.I$)$
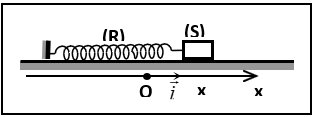
1) L'abscisse $x$ du solide $(S)$ dans le repère $(O\;,\ \vec{i})$ vérifie l'équation différentielle $$0.5\cdot \dfrac{d^{2}x}{\mathrm{d}t^{2}}+0.05\cdot\dfrac{\mathrm{d}x}{\mathrm{d}t}+5\cdot x=0$$
a) Que représente $h$ ?
Préciser son unité dans le système international.
b) Déterminer la masse $m$ du solide $(S)$ et la raideur $K$ du ressort.
2) On écarte le solide $(S)$ de sa position d'équilibre vers une position d'abscisse $x_{0}$ puis on le lâche sans vitesse initiale à l'origine des dates.
L'abscisse $x$ varie selon la courbe de la figure 1.
a) Déterminer graphiquement la pseudo période $T$ des oscillations et l'abscisse initiale $x_{0}$ du solide.
b) Établir l'expression de l'énergie mécanique du système $S_{0}\ :\ \{\text{Solide, ressort}\}$, le plan horizontal passant par le centre d'inertie $G$ du solide est pris comme plan de référence de l'énergie potentielle de pesanteur.
c) Montrer que la variation de l'énergie mécanique du système $S_{0}$ est égale au travail de $\overrightarrow{f}$
d) Calculer ce travail entre la date initiale $(t=0)$ et la date où le solide a effectué deux oscillations et demie.
3) Sur la figure 1) b) on a représenté les graphes des énergies en fonction du temps, identifier les courbes représentées et compléter la courbe qui manque.
4) On a répété l'expérience précédente pour $3$ valeurs différentes de $h$ tel que : $h_{1}=15$ ; $h_{2}=2$ et $h_{3}=5$ et on a représenté sur la figure 2 dans un ordre quelconque et à la même échelle, les variations de $X(t).$
a) Attribuer à chaque courbe la valeur de $h_{i}$ correspondante ?
b) Donner le nom de chaque régime observé.
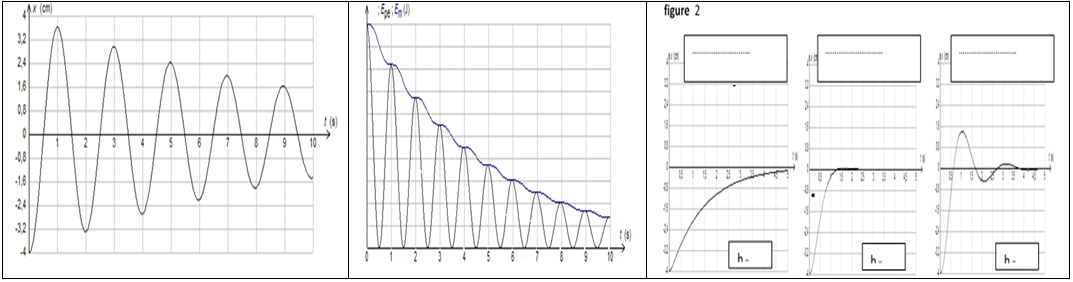
Exercice 14
L'extrémité d'un ressort $(R)$, est liée à un solide ponctuel de masse $m$, l'autre extrémité étant fixe.
Ce solide peut glisser sans frottement sur un plan horizontal.
Le ressort est à spires non jointives, de masse négligeable et de constante de raideur $k.$
On écarte le solide de sa position d'équilibre dans le sens positif d'une distance de $4\,cm$ puis on le lâche sans vitesse initiale.
La position d'équilibre est choisie comme origine du repère $(O\;,\ \vec{i}).$
1) a) Exprimer l'énergie mécanique à un instant $t$ quelconque du système $S$ : {Solide, ressort}.
b) Montrer que le mouvement solide est rectiligne sinusoïdal de pulsation $\omega_{0}.$
Donner l'expression de $\omega_{0}$
2) a) Déterminer l'expression de l'énergie cinétique $E_{C}$ du solide en fonction du temps.
Montrer que cette énergie est une fonction périodique.
b) Déterminer l'expression de l'énergie potentielle $E_{p}$ du système $S$ en fonction du temps.
Montrer que cette énergie est une fonction périodique.
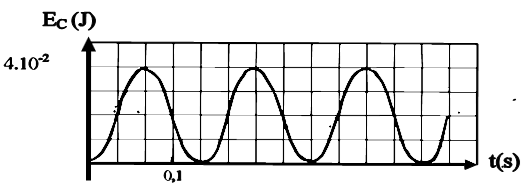
3) On donne la représentation graphique de l'énergie cinétique $E_{C}$ du solide en fonction du temps :
a) Déterminer la constante de raideur $k$ du ressort et la période $T_{0}$ de l'oscillateur.
b) Déterminer la masse $m$ du solide et l'équation horaire du mouvement du solide.
c) Représenter la courbe de l'énergie potentielle $E_{p}=f(t).$
Justifier le traçage de cette courbe.
Exercice 15
Un solide $(S)$ de masse $m$ est attaché à l'extrémité d'un ressort à spires non jointives de masse négligeable et de raideur $K=20N\cdot m^{-1}$, l'autre extrémité du ressort est attachée à un point fixe.
Le système $S_{0}=\{(S)+\text{ressort}\}$ est placé sur un plan horizontal (figure 1).
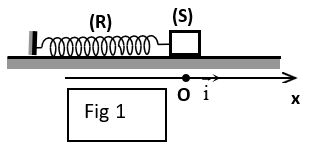
Au repos, le centre d'inertie $G$ du solide est au point $O$, origine d'un repère $(O\;,\ \vec{i})$ horizontal.
A partir de $O$, on écarte le solide $(S)$ d'une distance $X_{m}$ dans le sens positif et on le lâche sans vitesse.
1) a) Représenter les forces exercées sur le solide $(S)$ en mouvement à une date $t$ quelconque.
b. Établir l'équation différentielle du mouvement et déduire l'expression de la pulsation propre $\omega_{0}$ de l'oscillateur.
c) On donne le graphe représentant les variations de l'accélération du solide $(S)$ en fonction de l'élongation $x$ (figure 2).
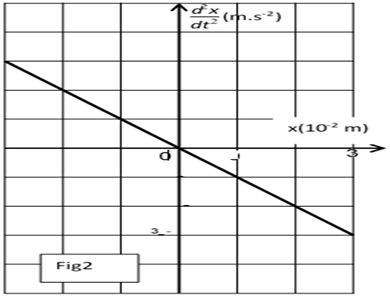
Déterminer graphiquement $\omega_{0}.$
Montrer que la masse du solide est $m=200g.$
2) a) Au passage du solide $(S)$ par une position d'abscisse $x$ sa vitesse est $v$, donner l'expression de l'énergie mécanique totale $E$ du système $S_{0}$ en fonction de $m$, $v$, $K$ et $x.$
b) Montrer que l'énergie $E$ est constante puis l'exprimer en fonction de $K$ et $Xm.$
3) On donne le graphe qui représente les variations de l'énergie cinétique $E_{c}$ du solide en fonction du temps (figure 3).
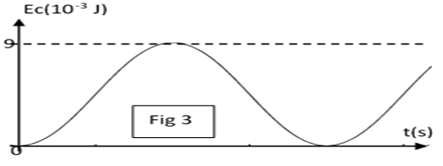
La loi horaire du mouvement est donnée par $x(t)=X_{m}\sin(\omega_{0}t+\varphi)$
a) Montrer que l'énergie cinétique $E_{c}$ s'écrit sous la forme $E_{c}=1/4KX^{2}m(1+\cos(2\omega_{0}t+2\varphi).$
b) A partir du graphe, déduire les valeurs de $X_{m}$ et $\varphi$ puis écrire, en fonction du temps, la loi horaire du mouvement
Exercice 16
Partie A
Un solide $(S)$ de masse $m$ est attaché à l'une des extrémités d'un ressort horizontal, parfaitement élastique, de constante de raideur $K$ et de masse négligeable devant celle du solide, l'autre extrémité du ressort étant fixe (fig 1).
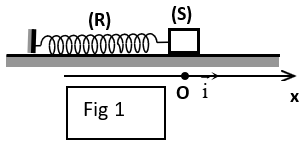
On étudie le mouvement du solide $(S)$ relativement à un repère galiléen $(o\;,\ \vec{i})$ horizontal, d'origine $O$ coïncidant avec la position d'équilibre du centre d'inertie du solide.
On écarte le solide $(S)$ de sa position d'équilibre dans le sens positif d'une distance $X_{m}=3\,cm$ puis on le lâche sans vitesse.
1) a) En appliquant la relation fondamentale de la dynamique au solide $(S)$, montrer que son mouvement est rectiligne sinusoïdal, de pulsation $\omega_{0}$ qu'on donnera son expression en fonction de $K$ et $m.$
b) A un instant $t$ quelconque, le centre d'inertie $G$ de $(S)$ a une élongation $x$ et sa vitesse instantané est $v.$
Établir l'expression de l'énergie mécanique $E$ du système $S_{0}=\{(S)+\text{ressort}\}$ en fonction $x$, $v$, $k$ et $m.$
c) Montrer que l'énergie $E$ est constante puis donner son expression en fonction de $k$ et $X_{m}.$
2) La solution de l'équation différentielle est $X(t)=X_{m}\sin(\omega_{0}t\varphi)$, déterminer l'expression de l'énergie potentielle $S_{0}$ en fonction de $K$, $X_{m}$, $\omega_{0}$, $t$ et $\varphi.$
Donner l'expression de sa période en fonction de $K$ et $m.$
3) On donne la représentation graphique de l'énergie potentielle $E_{p}$ (figure 2) en fonction du temps, déduire :
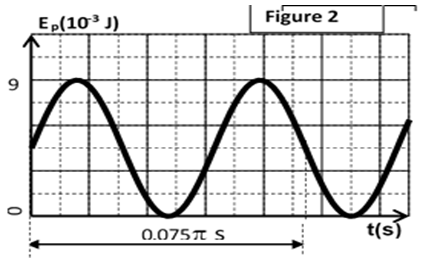
a) La constante de raideur $K$ du ressort et la période propre $T_{o}.$
Déduire la masse $m$ du solide.
b) la loi horaire de mouvement du solide $S$
Partie B
Dans cette partie, le solide $(S)$ est soumis à une force de frottement visqueux $\overrightarrow{f}=-h\overrightarrow{v}$ ou $h$ est une constante positive.
1) Établir l'équation différentielle de mouvement du solide $(S)$ régissant les variations de son élongation $X(t).$
2) Montrer que l'énergie totale du système $S_{0}=\{(S)+\text{ressort}\}$ n'est pas conservée.
3) A l'aide d'un dispositif approprié; on a enregistré les variation de l'élongation en fonction du temps ; on a trouvé le graphe de la figure 3 :
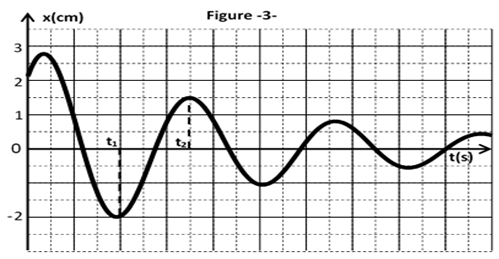
Calculer l'énergie dissipée par la force de frottement entre les instants $t_{1}$ et $t_{2}.$
Exercice 17
Un solide $(S)$ de masse $m$ est soudé à l'extrémité d'un ressort $(R)$ à spires non jointives de raideur $k.$
Le solide $(S)$ peut glisser sans frottement sur un plan horizontal.
Le centre d'inertie $G$ de $(S)$ est repéré sur un axe horizontal $X'OX$ dont $O$, l'origine, correspond à la position de repos de $(S).$
Le ressort est allongé à une abscisse $x_{0}$ et lâché à l'instant $t_{0}.$
Un dispositif permet d'enregistrer la variation de l'abscisse $X$ en fonction du temps donne la figure ci-dessous
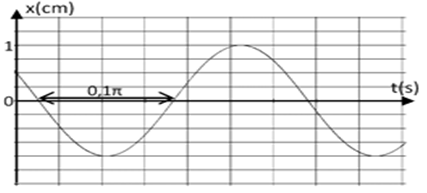
1) Déterminer à partir du graphe la période $T_{0}$ et la pulsation $\omega_{0}$ du mouvement ?
2) a) Établir l'équation différentielle du mouvement du solide.
En déduire une relation entre $\omega_{0}$, $m$ et $k.$
b) Établir l'équation horaire du mouvement de $(S).$
3) Donner l'expression de l'énergie potentielle élastique du système $\{\text{solide (S), ressort (R)}\}$ en fonction de $t.$
Sachant que cette valeur à l'instant $t=0s$ est égale à $6.25\cdot 10^{-4}j$
a) Déterminer la valeur de $k.$
b) Quelle est la valeur de la masse $m$ ?
4) On se propose d'augmenter la période propre $T_{0}$ de l'oscillateur tout en conservant $k$ et $X_{m}$, pour cela on remplace la masse de solide $(S)$ par $M>m.$
On donne la courbe de l'énergie potentielle élastique du système ${\text{solide }(S)\;,\text{ ressort }(R)}$ en fonction de $t.$
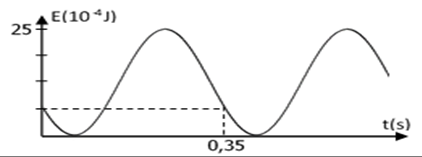
a) Déterminer la nouvelle période propre du système oscillateur $T$
b) En déduire la masse $M$
Exercice 18
On considère l'oscillateur mécanique représenté sur la figure ci-dessous :
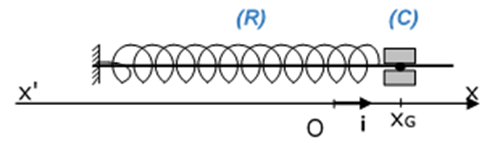
$(R)$ : ressort à spires non jointives, de masse négligeable et de raideur $K.$
$(C)$ : cylindre de masse $m$ pouvant glisser sans frottements sur une tige horizontale.
Écarté de sa position d'équilibre, puis libéré à lui-même, le solide se met à osciller.
A un instant de date $t$, le centre d'inertie du solide passe par la position d'abscisse $x$ relativement au repère $(O\;,\ \vec{i})$ avec la vitesse $v$
1) Établir l'équation différentielle vérifiée par la variable position $x(t)$
2) Vérifier que la solution de l'équation différentielle établie précédemment dans 1) est $x(t)=X_{m}\sin(\omega_{0}t+\varphi)$ ; en déduire l'expression de $\omega_{0}$
3) Un dispositif non représenté sur la figure a permis de tracer la courbe de la figure 2 donnant les variations de l'élongation $x$ en en fonction du temps.
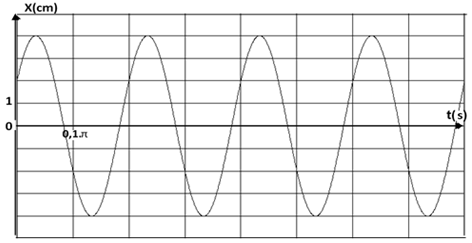
a) En exploitant la courbe, établir l'équation horaire $x(t)$
b) Déduire l'expression $v(t)$ de la vitesse instantanée.
Représenter $v(t)$ sur la figure 2 à l'échelle $1$ div $\rightarrow\ 0.1m\cdot s^{-1}.$
c) Montrer qu'à chaque instant, $x$ et $v$ vérifie la relation :
$100x^{2}+v^{2}=0.16$ avec $x$ en $m$ et $v$ en $m\cdot s^{-1}.$
d) Déterminer la valeur de la vitesse du centre d'inertie du solide quand ce dernier passe par le point d'abscisse $x=2cm$ dans le sens négatif
e) On donne la masse $m$ du cylindre $(m=100g)$ ; déterminer la raideur $K$ du ressort
4) a) Exprimer l'énergie mécanique $E$ du système (solide, ressort) en fonction de $x$ et $v$ et des caractéristiques de l'oscillateur.
b) Montrer que $E$ est constant et calculer sa valeur observée.
c) Monter que l'énergie mécanique de l'oscillateur n'est plus constante.

Commentaires
Abdourazak mous... (non vérifié)
jeu, 03/05/2020 - 21:28
Permalien
Reussir
Anonyme (non vérifié)
ven, 03/26/2021 - 01:20
Permalien
Correction
Kouassi Hermann (non vérifié)
mer, 04/07/2021 - 11:31
Permalien
Correction
Anonyme (non vérifié)
sam, 02/26/2022 - 00:57
Permalien
La correction svp
Anonyme (non vérifié)
mar, 03/01/2022 - 16:14
Permalien
Pour vérifier mes résultats
Mouhamed Diallo (non vérifié)
sam, 03/12/2022 - 22:32
Permalien
La reussite
Anonyme (non vérifié)
sam, 04/03/2021 - 02:26
Permalien
Intressant
Anonyme (non vérifié)
sam, 04/03/2021 - 17:26
Permalien
Correction
Ware Ndiaye (non vérifié)
dim, 04/11/2021 - 22:21
Permalien
etude
joseph (non vérifié)
jeu, 04/15/2021 - 19:13
Permalien
correction des excercices
Fallou (non vérifié)
dim, 04/18/2021 - 05:19
Permalien
Ndiaye
Tioyé koko (non vérifié)
dim, 07/04/2021 - 06:15
Permalien
Je demande la correction de certains exercices
Souleymane Diop (non vérifié)
lun, 08/16/2021 - 19:04
Permalien
Demande d'une autorisation de téléchargement des corrections
rahima (non vérifié)
mar, 12/21/2021 - 19:40
Permalien
Je voudrais avoir les corrections des exercices svp
Killua (non vérifié)
lun, 01/31/2022 - 00:49
Permalien
Correction svp
Moussa Gningue (non vérifié)
mer, 02/16/2022 - 14:17
Permalien
Je demande la correction svp
Anonyme (non vérifié)
mar, 03/01/2022 - 16:34
Permalien
Pour pratiquer beaucoup
Anonyme (non vérifié)
mer, 03/23/2022 - 17:37
Permalien
Je voudrais la correction de
Mahamadou (non vérifié)
sam, 03/26/2022 - 08:00
Permalien
Scientifique
Anonyme (non vérifié)
dim, 06/05/2022 - 15:26
Permalien
pdf
Anonyme (non vérifié)
dim, 02/26/2023 - 23:29
Permalien
bien
Anonyme (non vérifié)
lun, 03/20/2023 - 21:15
Permalien
Avoir la correction des exercices
Anonyme (non vérifié)
lun, 03/20/2023 - 21:28
Permalien
Je souhaite avoir la correction des exercices
Anonyme (non vérifié)
lun, 03/20/2023 - 21:28
Permalien
Je souhaite avoir la correction des exercices
Anonyme (non vérifié)
ven, 04/07/2023 - 09:38
Permalien
Correction exercice 10
Habsatou ndiaye (non vérifié)
ven, 04/07/2023 - 09:39
Permalien
C bien
Habsatou ndiaye (non vérifié)
ven, 04/07/2023 - 09:39
Permalien
C bien
Assale Kouakou ivon (non vérifié)
mer, 01/17/2024 - 11:16
Permalien
Exercices
Ajouter un commentaire