Application de la gravitation universelle au mouvement des satellites - Ts
Classe:
Terminale
I. Aspect dynamique
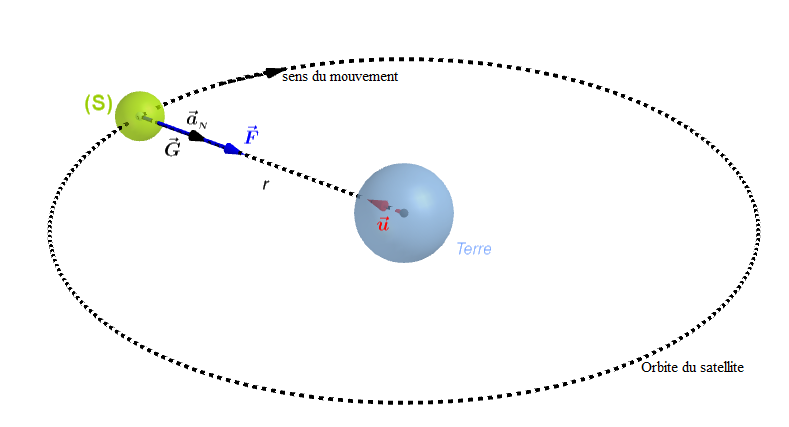
Soit un satellite $(S)$ de masse $m_{_{S}}$, en mouvement de rotation autour de la terre.
Supposons que sa trajectoire est circulaire.
Le système est constitué du satellite de masse $m_{_{S}}$ et le référentiel d'étude est le référentiel géocentrique considéré comme galiléen.
La seule force appliquée au système est la force d'attraction gravitationnelle $\vec{F}$ ; les frottements étant négligeables.
On a : $$\vec{F}=-\dfrac{\mathcal{G}.M_{_{T}}.m_{_{S}}}{r^{2}}\vec{u}$$
où $M_{_{T}}$ est la masse de la terre et $r$ ; le rayon de l'orbite du satellite.
En appliquant la deuxième loi de Newton, on obtient : $$\sum \vec{F}_{\text{ext}}=m_{_{S}}.\vec{a}$$
Soit : $$\vec{F}=m_{_{S}}.\vec{a}$$
Or, $\vec{F}=m_{_{S}}.\vec{G}\ $ donc, $m_{_{S}}.\vec{G}=m_{_{S}}.\vec{a}$
Par suite, $$\vec{G}=\vec{a}$$
Comme $\vec{G}$ est centripète alors, l'accélération $\vec{a}$ est normale.
Ainsi, sa composante tangentielle $\vec{a}_{_{T}}$ est nulle.
Or, $a_{_{T}}=\dfrac{\mathrm{d}v}{\mathrm{d}t}\ $ donc, $\dfrac{\mathrm{d}v}{\mathrm{d}t}=0\ $ ; c'est-à-dire la vitesse $v$ est une constante.
Par conséquent, le mouvement est uniforme.
D'où, le satellite est animé d'un mouvement circulaire uniforme.
II. Vitesse du satellite sur orbite
Le mouvement étant circulaire uniforme alors, $\ \vec{a}=\vec{a}_{_{N}}.$
Ainsi, $$\vec{G}=\vec{a}_{_{N}}\ \Rightarrow\ G=a_{_{N}}$$
Or, $\ G=\dfrac{\mathcal{G}.M_{_{T}}}{r^{2}}\ $ et $\ a_{_{N}}=\dfrac{v^{2}}{r}.$
Par suite,
$\begin{array}{rcl} G=a_{_{N}}&\Leftrightarrow&\dfrac{\mathcal{G}.M_{_{T}}}{r^{2}}=\dfrac{v^{2}}{r}\\ \\&\Leftrightarrow&v^{2}=\dfrac{\mathcal{G}.M_{_{T}}}{r}\\ \\&\Leftrightarrow&v=\sqrt{\dfrac{\mathcal{G}.M_{_{T}}}{r}}\quad\text{or, }\;\ G_{0}=\dfrac{\mathcal{G}.M_{_{T}}}{R_{_{T}}^{2}}\ \Rightarrow\ \mathcal{G}.M_{_{T}}=G_{0}.R_{_{T}}^{2}\\ \\&\Leftrightarrow&v=\sqrt{\dfrac{G_{0}.R_{_{T}}^{2}}{r}}\quad\text{or, }\;\ r=R_{_{T}}+z\\ \\&\Leftrightarrow&v=\sqrt{\dfrac{G_{0}.R_{_{T}}^{2}}{R_{_{T}}+z}}\\ \\&\Leftrightarrow&v=R_{_{T}}\sqrt{\dfrac{G_{0}}{R_{_{T}}+z}}\end{array}$
D'où, $$\boxed{v=R_{_{T}}\sqrt{\dfrac{G_{0}}{R_{_{T}}+z}}}\qquad(1)$$
où $z$ est l'altitude du satellite et $R_{_{T}}$, rayon de la terre.
III. Période du satellite sur orbite
Soit $T$ la période su satellite sur orbite.
On a : $T=\dfrac{2\pi}{\omega}$ avec $\omega$ la vitesse angulaire du satellite.
Or, $\ v=r.\omega\ $ donc, $\ \omega=\dfrac{v}{r}$
Par suite,
$\begin{array}{rcl} T&=&\dfrac{2\pi}{\omega}\\\\&=&\dfrac{2\pi}{\dfrac{v}{r}}\\ \\&=&\dfrac{2\pi.r}{v}\quad\text{or, }\;\ v=R_{_{T}}\sqrt{\dfrac{G_{0}}{r}}\\ \\&=&\dfrac{2\pi.r}{R_{_{T}}}\sqrt{\dfrac{r}{G_{0}}}\\ \\&=&\dfrac{2\pi}{R_{_{T}}}\sqrt{\dfrac{r^{3}}{G_{0}}}\quad\text{or, }\;\ r=R_{_{T}}+z\\ \\&=&\dfrac{2\pi}{R_{_{T}}}\sqrt{\dfrac{(R_{_{T}}+z)^{3}}{G_{0}}}\end{array}$
D'où, $$\boxed{T=\dfrac{2\pi}{R_{_{T}}}\sqrt{\dfrac{(R_{_{T}}+z)^{3}}{G_{0}}}}\qquad(2)$$
Satellite géostationnaire
Un satellite géostationnaire est un satellite ayant la même période de révolution que la terre : $$T=24\;h$$
Il est dit géostationnaire du fait qu'il est constamment en position fixe par rapport à la terre, dans le plan de l'équateur et son mouvement est uniforme par rapport à un référentiel géocentrique.
Ainsi, pour un observateur situé au niveau de l'équateur, le satellite semble ne pas bougé.
De la relation (2) on peut tirer l'altitude $z$ d'un satellite géostationnaire.
On a :
$\begin{array}{rcl} T=\dfrac{2\pi}{R_{_{T}}}\sqrt{\dfrac{(R_{_{T}}+z)^{3}}{G_{0}}}&\Rightarrow&T^{2}=\dfrac{4\pi^{2}(R_{_{T}}+z)^{3}}{R_{_{T}}^{2}.G_{0}}\\ \\&\Rightarrow&(R_{_{T}}+z)^{3}=\dfrac{T^{2}.R_{_{T}}^{2}.G_{0}}{4\pi^{2}}\quad\text{or, }\;\ G_{0}.R_{_{T}}^{2}=\mathcal{G}.M_{_{T}}\\ \\&\Rightarrow&(R_{_{T}}+z)^{3}=\dfrac{T^{2}.\mathcal{G}.M_{_{T}}}{4\pi^{2}}\\ \\&\Rightarrow&R_{_{T}}+z=\sqrt[3]{\dfrac{T^{2}.\mathcal{G}.M_{_{T}}}{4\pi^{2}}}\\ \\&\Rightarrow&z=\sqrt[3]{\dfrac{T^{2}.\mathcal{G}.M_{_{T}}}{4\pi^{2}}}+R_{_{T}}\end{array}$
D'où, $$\boxed{z=\sqrt[3]{\dfrac{T^{2}.\mathcal{G}.M_{_{T}}}{4\pi^{2}}}+R_{_{T}}}$$
A.N : $z=\sqrt[3]{\dfrac{86400^{2}\times 6.67\;10^{-11}\times 5.97\;10^{24}}{4\pi^{2}}}-64\;10^{5}=35826910.18\;m$
Soit : $\boxed{z\simeq 36000\;km}$
Troisième loi de Kepler - Loi des périodes
Le carré de la période de révolution est proportionnelle au cube du rayon de l'orbite : $$\dfrac{T^{2}}{r^{3}}=\text{constante}$$
On a :
$\begin{array}{rcl} T=\dfrac{2\pi}{R_{_{T}}}\sqrt{\dfrac{(R_{_{T}}+z)^{3}}{G_{0}}}&\Rightarrow&T^{2}=\dfrac{4\pi^{2}(R_{_{T}}+z)^{3}}{R_{_{T}}^{2}.G_{0}}\quad\text{or, }\;\ R_{_{T}}^{2}.G_{0}=\mathcal{G}.M_{_{T}}\\ \\&\Rightarrow&T^{2}=\dfrac{4\pi^{2}(R_{_{T}}+z)^{3}}{\mathcal{G}.M_{_{T}}}\quad\text{or, }\;\ R_{_{T}}+z=r\\ \\&\Rightarrow&T^{2}=\dfrac{4\pi^{2}.r^{3}}{\mathcal{G}.M_{_{T}}}\\ \\&\Rightarrow&\dfrac{T^{2}}{r^{3}}=\dfrac{4\pi^{2}}{\mathcal{G}.M_{_{T}}}\end{array}$
D'où, la troisième loi de Kepler : $$\boxed{\dfrac{T^{2}}{r^{3}}=\dfrac{4\pi^{2}}{\mathcal{G}.M_{_{T}}}=\text{constante}}\qquad(3)$$
III. Aspect énergétique
III.1. Énergie cinétique d'un satellite
Par définition on a : $E_{c}=\dfrac{1}{2}m_{_{S}}.v^{2}$
Or, d'après la relation (1) on a : $v^{2}=\dfrac{R_{_{T}}^{2}.G_{0}}{R_{_{T}}+z}$ avec $R_{_{T}}^{2}.G_{0}=\mathcal{G}.M_{_{T}}$
Donc, $v^{2}=\dfrac{\mathcal{G}.M_{_{T}}}{R_{_{T}}+z}$
D'où, $$\boxed{E_{c}=\dfrac{\mathcal{G}.M_{_{T}}.m_{_{S}}}{2(R_{_{T}}+z)}}\qquad(4)$$
III.2. Énergie potentielle d'un satellite
Considérons un satellite faisant un déplacement élémentaire de $dz$ par rapport à son altitude initiale.
Ainsi, le rayon $r$, de son orbite sera modifié de $dr.$
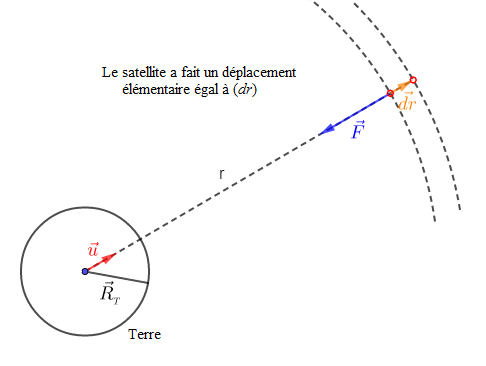
L'énergie potentielle du satellite est définie par : $\mathrm{d}E_{p}=-\mathrm{d}W(\vec{F})$
On a :
$\begin{array}{rcl} \mathrm{d}E_{p}&=&-\mathrm{d}W(\vec{F})\\\\&=&-\vec{F}\cdot\vec{\mathrm{d}r}\\\\&=&-F\cdot\mathrm{d}r\cdot\underbrace{\cos(\vec{F}\;,\ \vec{\mathrm{d}r})}_{=-1}\quad\text{or, }\;\ \widehat{(\vec{F}\;,\ \vec{\mathrm{d}r})}=\pi\\\\&=&F\cdot\mathrm{d}r\\ \\&=&\dfrac{\mathcal{G}.M_{_{T}}.m_{_{S}}}{r^{2}}\cdot\mathrm{d}r\end{array}$
Donc, $\mathrm{d}E_{p}=\dfrac{\mathcal{G}.M_{_{T}}.m_{_{S}}}{r^{2}}\cdot\mathrm{d}r$
Ainsi, par passage aux primitives ou par intégration, on obtient :
\begin{eqnarray} E_{p}&=&\int\mathrm{d}E_{p}\nonumber \\\\&=&\int\dfrac{\mathcal{G}.M_{_{T}}.m_{_{S}}}{r^{2}}\cdot\mathrm{d}r\nonumber \\\\&=&\mathcal{G}.M_{_{T}}.m_{_{S}}\int\dfrac{1}{r^{2}}\cdot\mathrm{d}r\quad\text{or, }\;\ \int\dfrac{1}{r^{2}}=-\dfrac{1}{r}+\text{cst}\nonumber \\\\&=&-\dfrac{\mathcal{G}.M_{_{T}}.m_{_{S}}}{r}+\text{cst}\nonumber\end{eqnarray}
Par suite, $E_{p}=-\dfrac{\mathcal{G}.M_{_{T}}.m_{_{S}}}{r}+\text{cst}$
Pour déterminer la constante on se réfère à l'état infini où l'énergie potentielle est nulle $(E_{p}(\infty)=0).$
Alors,
$\begin{array}{rcl} E_{p}(\infty)&=&E_{p_{(r\rightarrow\infty)}}\\ \\&=&\lim\limits_{r\rightarrow\infty}\left(-\dfrac{\mathcal{G}.M_{_{T}}.m_{_{S}}}{r}+\text{cst}\right)\quad\text{or, }\;\ \lim\limits_{r\rightarrow\infty}-\dfrac{\mathcal{G}.M_{_{T}}.m_{_{S}}}{r}=0\\ \\&=&\text{cst}\end{array}$
D'où, $\text{cst}=0$
Par conséquent, $$\boxed{E_{p}=-\dfrac{\mathcal{G}.M_{_{T}}.m_{_{S}}}{R_{_{T}}+z}}\qquad(5)$$
avec $R_{_{T}}+z=r$
III.3. Énergie mécanique d'un satellite
L'énergie mécanique $E_{m}$, d'un satellite sur orbite est donnée par : $$E_{m}=E_{c}+E_{p}$$
D'après les relation (4) et (5) on a :
$\begin{array}{rcl} E_{m}&=&E_{c}+E_{p}\\\\&=&\dfrac{\mathcal{G}.M_{_{T}}.m_{_{S}}}{2(R_{_{T}}+z)}-\dfrac{\mathcal{G}.M_{_{T}}.m_{_{S}}}{R_{_{T}}+z}\\ \\&=&-\dfrac{\mathcal{G}.M_{_{T}}.m_{_{S}}}{2(R_{_{T}}+z)}\end{array}$
D'où, $$\boxed{E_{m}=-\dfrac{\mathcal{G}.M_{_{T}}.m_{_{S}}}{2(R_{_{T}}+z)}}\qquad(6)$$
Remarque
$E_{m}=-E_{c}\;,\ E_{m}=\dfrac{E_{p}}{2}\ $ et par suite, $E_{p}=-2E_{c}$
IV. Satellisation
La satellisation est la mise sur orbite d'un satellite.
IV.1. $1^{er}$ vitesse cosmique ou vitesse de satellisation
C'est la vitesse qu'il faut communiquer à un objet à partir du sol pour le satelliser sur orbite basse.
Soit $v_{1}$ la $1^{er}$ vitesse cosmique d'un satellite.
Les frottements étant négligeables alors, la conservation de l'énergie mécanique permet d'écrire :
$$\begin{array}{rcl}\Delta E_{m}=0&\Rightarrow&E_{m_{(\text{initiale})}}=E_{m_{(\text{finale})}}\\ \\&\Rightarrow&\dfrac{1}{2}m_{_{S}}.v_{1}^{2}-\dfrac{\mathcal{G}.M_{_{T}}.m_{_{S}}}{R_{_{T}}}=E_{c_{(\text{finale})}}-\dfrac{\mathcal{G}.M_{_{T}}.m_{_{S}}}{R_{_{T}}+z}\quad\text{or, }\;\ E_{c}=-\dfrac{E_{p}}{2}\\ \\&\Rightarrow&\dfrac{1}{2}m_{_{S}}.v_{1}^{2}=\dfrac{\mathcal{G}.M_{_{T}}.m_{_{S}}}{2(R_{_{T}}+z)}-\dfrac{\mathcal{G}.M_{_{T}}.m_{_{S}}}{R_{_{T}}+z}+\dfrac{\mathcal{G}.M_{_{T}}.m_{_{S}}}{R_{_{T}}}\\ \\&\Rightarrow&v_{1}^{2}=\dfrac{2\mathcal{G}.M_{_{T}}}{R_{_{T}}}-\dfrac{\mathcal{G}.M_{_{T}}}{R_{_{T}}+z}\\ \\&\Rightarrow&v_{1}=\sqrt{2\mathcal{G}.M_{_{T}}\left(\dfrac{1}{R_{_{T}}}-\dfrac{1}{2(R_{_{T}}+z)}\right)}\end{array}$$
D'où, $$\boxed{v_{1}=\sqrt{2\mathcal{G}.M_{_{T}}\left(\dfrac{1}{R_{_{T}}}-\dfrac{1}{2(R_{_{T}}+z)}\right)}}\qquad(7)$$
IV.2. $2^{em}$ vitesse cosmique ou vitesse de libération
C'est la vitesse avec laquelle il faut lancer un objet, à partir du sol, pour qu'il échappe à l'attraction terrestre.
Soit $v_{2}$ la vitesse de libération d'un satellite.
A l'infini la vitesse du satellite est nulle, l'énergie potentielle aussi est nulle. Donc, $E_{m_{(\text{finale})}}=0$
Par suite, la conservation de l'énergie mécanique permet d'écrire :
$\begin{array}{rcl}\Delta E_{m}=0&\Rightarrow&E_{m_{(\text{initiale})}}=E_{m_{(\text{finale})}}\\ \\&\Rightarrow&\dfrac{1}{2}m_{_{S}}.v_{2}^{2}-\dfrac{\mathcal{G}.M_{_{T}}.m_{_{S}}}{R_{_{T}}}=0\\ \\&\Rightarrow&\dfrac{1}{2}m_{_{S}}.v_{2}^{2}=\dfrac{\mathcal{G}.M_{_{T}}.m_{_{S}}}{R_{_{T}}}\\ \\&\Rightarrow&v_{2}^{2}=\dfrac{2\mathcal{G}.M_{_{T}}}{R_{_{T}}}\\ \\&\Rightarrow&v_{2}=\sqrt{\dfrac{2\mathcal{G}.M_{_{T}}}{R_{_{T}}}}\end{array}$
Ainsi, $$\boxed{v_{2}=\sqrt{\dfrac{2\mathcal{G}.M_{_{T}}}{R_{_{T}}}}}\qquad(8)$$
A.N : $v_{2}=\sqrt{\dfrac{2\times 6.67\;10^{-11}\times 5.97\;10^{24}}{64\;10^{5}}}=11.15\;10^{3}\;m.s^{-1}$
D'où, $\boxed{v_{2}=11.15\;km.s^{-1}}$
V. Impesanteur dans un satellite sur orbite
Un corps est en état d'impesanteur lorsque son poids semble disparaître (poids apparent ou réaction est nul).
Considérons un satellite sur orbite et soit un corps de masse $m$ placé à l'intérieur, en un point $A.$
Ce corps semble alors flotter du fait que son poids apparent est nul.
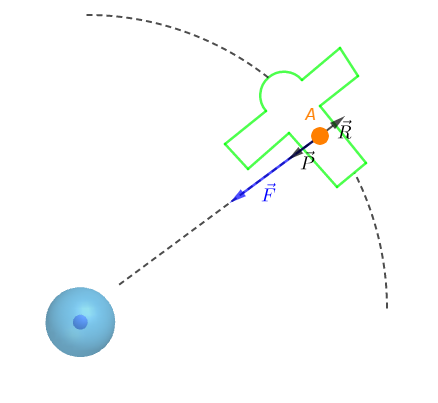
$-\ \ $ Par rapport au satellite, le corps de masse $m$ est immobile et les forces appliquées sont le poids $\vec{P}$ et la réaction $\vec{R}$, du support.
On obtient alors : $$\vec{P}+\vec{R}=\vec{0}\qquad(*)$$
$-\ \ $ Par rapport à un référentiel géocentrique supposé galiléen, ce corps en mouvement suivant la même accélération que le satellite, est soumis à la force d'interaction gravitationnelle $\vec{F}$ et à la réaction $\vec{R}.$
En appliquant la troisième loi de Newton, on obtient : $$\vec{F}+\vec{R}=m.\vec{a}$$
Or, $\ \vec{F}=m.\vec{G}\ $ ce qui donne alors, $$m.\vec{G}+\vec{R}=m.\vec{a}\qquad(**)$$
Par ailleurs, on sait que $\vec{G}=\vec{a}$
Donc, l'équation (**) devient : $m.\vec{a}+\vec{R}=m.\vec{a}$
D'où, $$\vec{R}=\vec{0}$$
Par suite, en reportant dans l'équation (*), on trouve $$\vec{P}=\vec{0}$$
Par conséquent, ce corps de masse $m$ est en état d'impesanteur.

Ajouter un commentaire