Solution des exercices : Racine carrée 3e
Classe:
Troisième
Exercice 1
Donnons une écriture simple des nombres réels $A\;,\ B\;,\ C\;,\ D\ $ et $\ E$ suivants :
Soit $A=\sqrt{200}-3\sqrt{18}+6\sqrt{2}+50$
Alors, dans l'écriture de $A$, nous allons remplacer $\sqrt{200}\ $ et $\ \sqrt{18}$ par une écriture plus simple.
On a :
$\begin{array}{rcl} \sqrt{200}&=&\sqrt{100\times 2}\\\\&=&\sqrt{100}\times\sqrt{2}\\\\&=&10\sqrt{2}\end{array}$
et
$\begin{array}{rcl} \sqrt{18}&=&\sqrt{9\times 2}\\\\&=&\sqrt{9}\times\sqrt{2}\\\\&=&3\sqrt{2}\end{array}$
Donc, en remplaçant $\sqrt{200}$ par $10\sqrt{2}\ $ et $\ \sqrt{18}$ par $3\sqrt{2}$, on obtient :
$\begin{array}{rcl} A&=&\sqrt{200}-3\sqrt{18}+6\sqrt{2}+50\\\\&=&10\sqrt{2}-3\times 3\sqrt{2}+6\sqrt{2}+50\\\\&=&10\sqrt{2}-9\sqrt{2}+6\sqrt{2}+50 \\ \\&=&7\sqrt{2}+50\end{array}$
D'où, $\boxed{A=7\sqrt{2}+50}$
Soit $B=(\sqrt{2}+2)^{2}$
En appliquant la règle des identités remarquables $(a+b)^{2}=a^{2}+2ab+b^{2}$ avec $a=\sqrt{2}\ $ et $\ b=2$, on obtient :
$\begin{array}{rcl} B&=&(\sqrt{2}+2)^{2}\\\\&=&(\sqrt{2})^{2}+2\times 2\times\sqrt{2}+2^{2}\\ \\&=&2+4\sqrt{2}+4\\\\ &=&6+4\sqrt{2}\end{array}$
D'où, $\boxed{B=6+4\sqrt{2}}$
Soit $C=(3\sqrt{2}-5)^{2}$
On applique la règle $(a-b)^{2}=a^{2}-2ab+b^{2}$ avec $a=3\sqrt{2}\ $ et $\ b=5$
Donc, on a :
$\begin{array}{rcl} C&=&(3\sqrt{2}-5)^{2}\\\\&=&(3\sqrt{2})^{2}-2\times 5\times 3\sqrt{2}+(-5)^{2}\\\\&=&(3)^{2}\times(\sqrt{2})^{2}-30\sqrt{2}+25\\\\&=&9\times 2-30\sqrt{2}+25\\\\ &=&18-30\sqrt{2}+25\\ \\&=&43-30\sqrt{2}\end{array}$
D'où, $\boxed{C=43-30\sqrt{2}}$
On donne $D=(3\sqrt{2}+5)(3\sqrt{2}-5)$
On applique la règle $(a-b)(a+b)=a^{2}-b^{2}$ avec $a=3\sqrt{2}\ $ et $\ b=5$
Ainsi,
$\begin{array}{rcl} D&=&(3\sqrt{2}+5)(3\sqrt{2}-5)\\\\&=&(3\sqrt{2})^{2}-(5)^{2}\\\\&=&(3)^{2}\times(\sqrt{2})^{2}-25\\\\&=&9\times 2-25\\\\&=&18-25\\\\ &=&-7\end{array}$
D'où, $\boxed{D=-7}$
Soit, $E=\sqrt{19-\sqrt{1+\sqrt{8^{2}}}}$
On calcule :
$-\ $ d'abord, $\sqrt{8^{2}}$
On a : $\sqrt{8^{2}}=|8|=8$
$-\ $ ensuite, $\sqrt{1+\sqrt{8^{2}}}$
Comme $\sqrt{8^{2}}=8$ alors,
$\begin{array}{rcl} \sqrt{1+\sqrt{8^{2}}}&=&\sqrt{1+8}\\\\&=&\sqrt{9}\\\\&=&3\end{array}$
$-\ $ enfin, $\sqrt{19-\sqrt{1+\sqrt{8^{2}}}}$
On sait que $\sqrt{1+\sqrt{8^{2}}}=3$ donc,
$\begin{array}{rcl} \sqrt{19-\sqrt{1+\sqrt{8^{2}}}}&=&\sqrt{19-3}\\\\&=&\sqrt{16}\\\\&=&4\end{array}$
D'où, $\boxed{E=4}$
Exercice 2
1) $\sqrt{40}=20\;,\quad (Faux)$
En effet, $(\sqrt{40})^{2}=40$ et $20^{2}=400$
Or, $400\neq 40$ donc $\sqrt{40}\neq 20$
2) $7\sqrt{2}=\sqrt{98}\;,\quad (Vrai)$
On a : $\sqrt{98}=\sqrt{49\times 2}=\sqrt{49}\times\sqrt{2}=7\sqrt{2}$
3) $\sqrt{64+25}=8+5=13\quad (Faux)$
On sait que $64+25=89$ et que $13^{2}=169$
$169\neq 89$ donc, $\sqrt{64+25}\neq 13$
Aussi, $\sqrt{64+25}$ n'est pas égale à $\sqrt{64}+\sqrt{25}$
Exercice 3
On considère les nombres réels définis par :
$$X=\dfrac{\sqrt{5}}{\sqrt{5}-\sqrt{3}}-\dfrac{\sqrt{3}}{\sqrt{5}+\sqrt{3}}\quad\text{et}\quad Y=(3\sqrt{2}-\sqrt{3})^{2}+6\sqrt{6}$$
Montrons que $X\ $ et $\ Y$ sont des nombres entiers naturels.
On a : $X=\dfrac{\sqrt{5}}{\sqrt{5}-\sqrt{3}}-\dfrac{\sqrt{3}}{\sqrt{5}+\sqrt{3}}$
En réduisant au même dénominateur on obtient :
$\begin{array}{rcl} X&=&\dfrac{\sqrt{5}}{\sqrt{5}-\sqrt{3}}-\dfrac{\sqrt{3}}{\sqrt{5}+\sqrt{3}}\\ \\&=&\dfrac{\sqrt{5}(\sqrt{5}+\sqrt{3})-\sqrt{3}(\sqrt{5}-\sqrt{3})}{(\sqrt{5}-\sqrt{3})(\sqrt{5}+\sqrt{3})} \\ \\&=&\dfrac{\sqrt{5}\times\sqrt{5}+\sqrt{5}\times\sqrt{3}-\sqrt{3}\times\sqrt{5}-\sqrt{3}\times(-\sqrt{3})}{(\sqrt{5})^{2}-(\sqrt{3})^{2}} \\ \\&=&\dfrac{5+\sqrt{15}-\sqrt{15}+3}{5-3} \\ \\&=&\dfrac{5+3}{2}\\\\&=&\dfrac{8}{2} \\ \\&=&4 \end{array}$
Donc, $\boxed{X=4\quad\text{qui est bien un entier naturel}}$
Soit : $Y=(3\sqrt{2}-\sqrt{3})^{2}+6\sqrt{6}$
On a :
$\begin{array}{rcl} Y&=&(3\sqrt{2}-\sqrt{3})^{2}+6\sqrt{6}\\ \\&=&(3\sqrt{2})^{2}-2\times 3\sqrt{2}\times\sqrt{3}+(\sqrt{3})^{2}+6\sqrt{6}\\ \\&=&18-6\sqrt{2\times 3}+3+6\sqrt{6}\\ \\&=&21-6\sqrt{6}+6\sqrt{6}\\ \\&=&21\end{array}$
Donc, $\boxed{Y=21\quad\text{qui est bien un entier naturel}}$
Exercice 4
On donne les nombres réels suivants tels que :
$$X=\sqrt{4+\sqrt{7}}-\sqrt{4-\sqrt{7}}\quad\text{et}\quad Y=\sqrt{3-2\sqrt{2}}-\sqrt{3+2\sqrt{2}}$$
1) Déterminons les signes respectifs de $X\ $ et $\ Y.$
Pour déterminer le signe de $X$ on compare les nombres $\sqrt{4+\sqrt{7}}\ $ et $\ \sqrt{4-\sqrt{7}}.$
On a : $\sqrt{4+\sqrt{7}}>0\ $ et $\ \sqrt{4-\sqrt{7}}>0$
Soit alors : $(\sqrt{4+\sqrt{7}})^{2}=4+\sqrt{7}\ $ et $\ (\sqrt{4-\sqrt{7}})^{2}=4-\sqrt{7}$
Or, $4+\sqrt{7}>4-\sqrt{7}$
Donc, le nombre $\sqrt{4+\sqrt{7}}$ est supérieur au nombre $\sqrt{4-\sqrt{7}}.$
D'où, $X$ est positif
De même, pour déterminer le signe de $Y$ on compare les nombres $\sqrt{3-2\sqrt{2}}\ $ et $\ \sqrt{3+2\sqrt{2}}.$
On a : $\sqrt{3-2\sqrt{2}}>0\ $ et $\ \sqrt{3+2\sqrt{2}}>0$
Alors : $(\sqrt{3-2\sqrt{2}})^{2}=3-2\sqrt{2}\ $ et $\ (\sqrt{3+2\sqrt{2}})^{2}=3+2\sqrt{2}$
Or, $3-2\sqrt{2}<3+2\sqrt{2}$
Donc, le nombre $\sqrt{3-2\sqrt{2}}$ est inférieur au nombre $\sqrt{3+2\sqrt{2}}.$
D'où, $Y$ est négatif
2) Calculons $X^{2}\ $ et $\ Y^{2}.$
On a : $X=\sqrt{4+\sqrt{7}}-\sqrt{4-\sqrt{7}}$
Donc,
$\begin{array}{rcl} X^{2}&=&\left(\sqrt{4+\sqrt{7}}-\sqrt{4-\sqrt{7}}\right)^{2}\\ \\&=&\left(\sqrt{4+\sqrt{7}}\right)^{2}-2\times\left(\sqrt{4+\sqrt{7}}\right)\times\left(\sqrt{4-\sqrt{7}}\right)+\left(\sqrt{4-\sqrt{7}}\right)^{2}\\ \\&=&(4+\sqrt{7})-2\times\sqrt{(4+\sqrt{7})(4-\sqrt{7})}+(4-\sqrt{7})\\ \\&=&(4+\sqrt{7})+(4-\sqrt{7})-2\times\sqrt{(4)^{2}-(\sqrt{7})^{2}} \\ \\&=&8-2\times\sqrt{16-7} \\ \\&=&8-2\times\sqrt{9} \\ \\&=&8-2\times 3\\\\&=&8-6\\ \\&=&2\end{array}$
D'où, $\boxed{X^{2}=2}$
De même, on a : $Y=\sqrt{3-2\sqrt{2}}-\sqrt{3+2\sqrt{2}}$
Donc,
$\begin{array}{rcl} Y^{2}&=&\left(\sqrt{3-2\sqrt{2}}-\sqrt{3+2\sqrt{2}}\right)^{2}\\ \\&=&\left(\sqrt{3-2\sqrt{2}}\right)^{2}-2\times\left(\sqrt{3-2\sqrt{2}}\right)\times\left(\sqrt{3+2\sqrt{2}}\right)+\left(\sqrt{3+2\sqrt{2}}\right)^{2}\\ \\&=&(3-2\sqrt{2})-2\times\sqrt{(3-2\sqrt{2})(3+2\sqrt{2})}+(3+2\sqrt{2})\\ \\&=&(3-2\sqrt{2})+(3+2\sqrt{2})-2\times\sqrt{(3)^{2}-(2\sqrt{2})^{2}} \\ \\&=&6-2\times\sqrt{9-8} \\ \\&=&6-2\times\sqrt{1} \\ \\&=&6-2\\ \\&=&4\end{array}$
D'où, $\boxed{Y^{2}=4}$
3) En déduisons $X\ $ et $\ Y.$
On a : $X^{2}=2$
Alors, $\sqrt{X^{2}}=\sqrt{2}\ $ or, on sait que $\sqrt{X^{2}}=|X|$
Donc, $|X|=\sqrt{2}$
Mais comme $X$ est positif alors, $|X|=X$
D'où, $\boxed{X=\sqrt{2}}$
De même, on a : $Y^{2}=4$
Alors, $\sqrt{Y^{2}}=\sqrt{4}=2\ $ or, on sait que $\sqrt{Y^{2}}=|Y|$
Donc, $|Y|=2$
$Y$ étant négatif alors, $|Y|=-Y$
Donc, $-Y=2$
D'où, $\boxed{Y=-2}$
Soit $3\sqrt{2}-4$ l'expression conjuguée de $3\sqrt{2}+4$
D'où, $\boxed{b=\dfrac{3\sqrt{2}}{2}-2}$
Exercice 5
L'unité de longueur est le $hm.$ Les dimensions d'un champ rectangulaire sont : $2\sqrt{3}+2\ $ et $\ 2\sqrt{3}-2.$
Calculons : Le périmètre, l'aire ensuite, le diamètre du cercle circonscrit de ce champ rectangulaire.
Soit $L$ la longueur du champ et $\ell$ sa largeur.
Alors, on a : $L=2\sqrt{3}+2\ $ et $\ \ell=2\sqrt{3}-2$
Ainsi,
$-\ $ le périmètre $p$ du champ est donné par :
$\begin{array}{rcl} p&=&2\times(L+\ell)\\\\&=&2\times((2\sqrt{3}+2)+(2\sqrt{3}-2))\\\\&=&2\times(2\sqrt{3}+2\sqrt{3}+2-2)\\\\&=&2\times(4\sqrt{3})\\\\&=&8\sqrt{3} \end{array}$
D'où, $\boxed{p=8\sqrt{3}\;hm}$
$-\ $ l'aire $\mathcal{A}$ du champ est donnée par :
$\begin{array}{rcl}\mathcal{A}&=&L\times\ell\\\\&=&(2\sqrt{3}+2)\times(2\sqrt{3}-2)\\\\&=&(2\sqrt{3})^{2}-(2)^{2}\\\\&=&(4\times 3)-4\\\\&=&12-4\\\\&=&8\end{array}$
Donc, $\boxed{\mathcal{A}=8\;hm^{2}}$
$-\ $ le cercle circonscrit a pour diamètre l'une des diagonales du rectangle.
D'après le théorème de Pythagore, on a :
$$d^{2}=L^{2}+\ell^{2}$$
Ce qui entraine :
$\begin{array}{rcl} d&=&\sqrt{L^{2}+\ell^{2}}\\\\&=&\sqrt{(2\sqrt{3}+2)^{2}+(2\sqrt{3}-2)^{2}}\\\\&=&\sqrt{(2\sqrt{3})^{2}+2\times 2\times 2\sqrt{3}+2^{2}+(2\sqrt{3})^{2}-2\times 2\times 2\sqrt{3}+2^{2}}\\\\&=&\sqrt{12+8\sqrt{3}+4+12-8\sqrt{3}+4}\\\\&=&\sqrt{32}\\\\&=&\sqrt{16\times 2}\\\\&=&4\sqrt{2}\end{array}$
D'où, $\boxed{d=4\sqrt{2}\;hm}$
Exercice 6 "BFEM 2009"
On donne les réels : $a=2-\dfrac{3\sqrt{2}}{2}\ $ et $\ b=\dfrac{1}{3\sqrt{2}+4}$
1) Rendons rationnel le dénominateur de $b.$
Soit $3\sqrt{2}-4$ l'expression conjuguée de $3\sqrt{2}+4$
Rendre rationnel le dénominateur de $b$ revient tout simplement à multiplier le numérateur et le dénominateur de $b$ par le même nombre $3\sqrt{2}-4.$
On a :
$\begin{array}{rcl} b&=&\dfrac{1}{3\sqrt{2}+4}\\ \\&=&\dfrac{1\times(3\sqrt{2}-4)}{(3\sqrt{2}+4)(3\sqrt{2}-4)} \\ \\&=&\dfrac{3\sqrt{2}-4}{(3\sqrt{2})^{2}-(4)^{2}} \\ \\&=&\dfrac{3\sqrt{2}-4}{18-16} \\ \\&=&\dfrac{3\sqrt{2}-4}{2}\\ \\&=&\dfrac{3\sqrt{2}}{2}-2 \end{array}$
D'où, $\boxed{b=\dfrac{3\sqrt{2}}{2}-2}$
Montrons que les nombres $a\ $ et $\ b$ sont des opposés.
$a\ $ et $\ b$ non nuls sont opposés si, et seulement si, $a=-b$
Ou tout simplement $a\ $ et $\ b$ sont opposés s'ils vérifient $a+b=0$
Donc, si on a $a+b=0$ alors, on conclut que $a\ $ et $\ b$ sont opposés.
On a :
$\begin{array}{rcl} a+b&=&\left(2-\dfrac{3\sqrt{2}}{2}\right)+\left(\dfrac{1}{3\sqrt{2}+4}\right)\\ \\&=&\left(2-\dfrac{3\sqrt{2}}{2}\right)+\left(\dfrac{3\sqrt{2}}{2}-2\right)\\ \\&=&2-\dfrac{3\sqrt{2}}{2}+\dfrac{3\sqrt{2}}{2}-2\\ \\&=&2-2+\dfrac{3\sqrt{2}}{2}-\dfrac{3\sqrt{2}}{2}\\ \\&=&0\end{array}$
Ce qui montre que $a\ $ et $\ b$ sont opposés.
2) Soit $A=\sqrt{(1-2\sqrt{2})^{2}}+(\sqrt{2}-2)^{2}-\sqrt{18}.$
Montrons que $A=5-5\sqrt{2}$
On a : $A=\sqrt{(1-2\sqrt{2})^{2}}+(\sqrt{2}-2)^{2}-\sqrt{18}=|1-2\sqrt{2}|+(\sqrt{2}-2)^{2}-\sqrt{2\times 9}$
Cherchons le signe de $1-2\sqrt{2}$
On a : $1^{2}=1\ $ et $\ (2\sqrt{2})^{2}=4\times 2=8$
On remarque que $8>1$ donc, $1<2\sqrt{2}$
D'où, $1-2\sqrt{2}<0$
Ainsi, $|1-2\sqrt{2}|=-(1-2\sqrt{2})=2\sqrt{2}-1$
Donc,
$\begin{array}{rcl} A&=&|1-2\sqrt{2}|+(\sqrt{2}-2)^{2}-\sqrt{2\times 9}\\ \\&=&2\sqrt{2}-1+(\sqrt{2})^{2}-2\times\sqrt{2}\times 2+(2)^{2}-3\sqrt{2}\\ \\&=&2\sqrt{2}-1+2-4\sqrt{2}+4-3\sqrt{2}\\ \\&=&5-5\sqrt{2}\end{array}$
D'où $\boxed{A=5-5\sqrt{2}}$
Encadrons $A\ $ à $10^{-2}$ prés sachant que :
$$1.414<\sqrt{2}<1.415.$$
On a : $1.414<\sqrt{2}<1.415$ alors, multiplions chaque membre par $-5$ tout en sachant que les inégalités changent de sens ;
$$-5\times 1.414>-5\sqrt{2}>-5\times 1.415$$
$$-5\times 1.414>-5\sqrt{2}>-5\times 1.415$$
Ce qui donne : $-7.07>-5\sqrt{2}>-7.075$
En ajoutant $5$ à chaque membre on obtient :
$$5-7.07>5-5\sqrt{2}>5-7.075$$
Donc, $-2.07>5-5\sqrt{2}>-2.075$
D'où,
$$-2.075<5-5\sqrt{2}<-2.07$$
Par suite,
$$-2.08<5-5\sqrt{2}<-2.07\ \text{ à }\ 10^{-2}\ \text{ prés}$$
$$-2.075<5-5\sqrt{2}<-2.07$$
Par suite,
$$-2.08<5-5\sqrt{2}<-2.07\ \text{ à }\ 10^{-2}\ \text{ prés}$$
Ainsi, un encadrement de $A\ $ à $10^{-2}$ prés est donné par :
$$\boxed{-2.08<A<-2.07}$$
Exercice 7
1) Calculons la valeur numérique de l'expression suivante : $$C=\dfrac{2x}{2-x}-\dfrac{2-x}{x}\quad\text{ pour }x=2-\sqrt{3}$$
Cela revient donc à remplacer $x$ par $2-\sqrt{3}$ dans l'expression de $C.$
On a alors :
$\begin{array}{rcl} C&=&\dfrac{2\times(2-\sqrt{3})}{2-(2-\sqrt{3})}-\dfrac{2-(2-\sqrt{3})}{2-\sqrt{3}}\\\\&=&\dfrac{2\times(2-\sqrt{3})}{2-2+\sqrt{3}}-\dfrac{2-2+\sqrt{3}}{2-\sqrt{3}}\\\\&=&\dfrac{2\times(2-\sqrt{3})}{\sqrt{3}}-\dfrac{\sqrt{3}}{2-\sqrt{3}}\\\\&=&\dfrac{2\times(2-\sqrt{3})(2-\sqrt{3})-(\sqrt{3})\times(\sqrt{3})}{(2-\sqrt{3})\sqrt{3}}\\\\&=&\dfrac{2\times(2-\sqrt{3})^{2}-(\sqrt{3})^{2}}{2\sqrt{3}-(\sqrt{3})^{2}}\\\\&=&\dfrac{2\times(4-4\sqrt{3}+3)-3}{2\sqrt{3}-3}\\\\&=&\dfrac{14-8\sqrt{3}-3}{2\sqrt{3}-3}\\\\&=&\dfrac{11-8\sqrt{3}}{2\sqrt{3}-3}\end{array}$
Donc, pour $x=2-\sqrt{3}$, on trouve : $\boxed{C=\dfrac{11-8\sqrt{3}}{2\sqrt{3}-3}}$
2) Écrivons les expressions suivantes sous la forme $a\sqrt{b}$ avec $a\in\mathbb{Q}\ $ et $\ b\in\mathbb{N}$
Soit $A=\sqrt{363}+5\sqrt{3}+\sqrt{2}\times\sqrt{54}-3\sqrt{12}$
Alors, il suffit de mettre certains termes sous une forme plus simple puis, de calculer.
On a :
$\begin{array}{rcl} \sqrt{363}&=&\sqrt{121\times 3}\\\\&=&\sqrt{121}\times\sqrt{3}\\\\&=&11\sqrt{3}\end{array}$
$\begin{array}{rcl} \sqrt{54}&=&\sqrt{9\times 6}\\\\&=&\sqrt{9}\times\sqrt{2\times 3}\\\\&=&3\sqrt{2}\times\sqrt{3}\end{array}$
$\begin{array}{rcl} \sqrt{12}&=&\sqrt{4\times 3}\\\\&=&\sqrt{4}\times\sqrt{3}\\\\&=&2\sqrt{3}\end{array}$
Donc, en remplaçant dans l'expression de $A\;,\ \sqrt{363}\;,\ \sqrt{54}\ $ et $\ \sqrt{12}$ par leur valeur, on obtient :
$\begin{array}{rcl} A&=&\sqrt{363}+5\sqrt{3}+\sqrt{2}\times\sqrt{54}-3\sqrt{12}\\\\&=&11\sqrt{3}+5\sqrt{3}+\sqrt{2}\times 3\times\sqrt{2}\times\sqrt{3}-3\times 2\sqrt{3}\\\\&=&11\sqrt{3}+5\sqrt{3}+3\times\sqrt{2}\times\sqrt{2}\times\sqrt{3}-6\sqrt{3}\\\\&=&11\sqrt{3}+5\sqrt{3}+3\times 2\times\sqrt{3}-6\sqrt{3}\\\\&=&11\sqrt{3}+5\sqrt{3}+6\sqrt{3}-6\sqrt{3}\\\\&=&16\sqrt{3}\end{array}$
D'où, $\boxed{A=16\sqrt{3}}$
Soit $B=\sqrt{20}-\dfrac{2}{3}\sqrt{80}+7\sqrt{2.45}$
On sait que :
$20=4\times 5$
$80=16\times 5$
$2.45=\dfrac{245}{100}=\dfrac{49\times 5}{100}$
Donc, en remplaçant, on obtient :
$\begin{array}{rcl} B&=&\sqrt{20}-\dfrac{2}{3}\sqrt{80}+7\sqrt{2.45}\\\\&=&\sqrt{4\times 5}-\dfrac{2}{3}\sqrt{16\times 5}+7\sqrt{\dfrac{49\times 5}{100}}\\\\&=&\sqrt{4}\times\sqrt{5}-\dfrac{2}{3}\sqrt{16}\times\sqrt{5}+7\dfrac{\sqrt{49\times 5}}{\sqrt{100}}\\\\&=&2\times\sqrt{5}-\dfrac{2}{3}\times 4\times\sqrt{5}+7\dfrac{\sqrt{49}\times\sqrt{5}}{10}\\\\&=&2\sqrt{5}-\dfrac{8}{3}\sqrt{5}+\dfrac{7\times 7\times\sqrt{5}}{10}\\\\&=&2\sqrt{5}-\dfrac{8}{3}\sqrt{5}+\dfrac{49}{10}\sqrt{5}\\\\&=&\dfrac{60}{30}\sqrt{5}-\dfrac{80}{30}\sqrt{5}+\dfrac{147}{30}\sqrt{5}\\\\&=&\dfrac{(60-80+147)}{30}\sqrt{5}\\\\&=&\dfrac{127}{30}\sqrt{5}\end{array}$
Ainsi, $\boxed{B=\dfrac{127}{30}\sqrt{5}}$
Soit $C=2\sqrt{75}-4\sqrt{48}+7\sqrt{192}$
On sait que :
$75=25\times 3$
$48=16\times 3$
$192=64\times 3$
Donc, en remplaçant, on obtient :
$\begin{array}{rcl} C&=&2\sqrt{75}-4\sqrt{48}+7\sqrt{192}\\\\&=&2\sqrt{25\times 3}-4\sqrt{16\times 3}+7\sqrt{64\times 3}\\\\&=&2\sqrt{25}\times\sqrt{3}-4\sqrt{16}\times\sqrt{3}+7\sqrt{64}\times\sqrt{3}\\\\&=&2\times 5\times\sqrt{3}-4\times 4\times\sqrt{3}+7\times 8\times\sqrt{3}\\\\&=&10\sqrt{3}-16\sqrt{3}+56\sqrt{3}\\\\&=&50\sqrt{3}\end{array}$
D'où, $\boxed{C=50\sqrt{3}}$
Soit $D=-15\sqrt{96}+18\sqrt{54}+3\sqrt{486}-21\sqrt{24}$
Alors, on sait que :
$96=16\times 6$
$54=9\times 6$
$486=81\times 6$
$24=4\times 6$
Donc, en remplaçant, on trouve :
$\begin{array}{rcl} D&=&-15\sqrt{96}+18\sqrt{54}+3\sqrt{486}-21\sqrt{24}\\\\&=&-15\sqrt{16\times 6}+18\sqrt{9\times 6}+3\sqrt{81\times 6}-21\sqrt{4\times 6}\\\\&=&-15\sqrt{16}\times\sqrt{6}+18\sqrt{9}\times\sqrt{6}+3\sqrt{81}\times\sqrt{6}-21\sqrt{4}\times\sqrt{6}\\\\&=&-15\times 4\times\sqrt{6}+18\times 3\times\sqrt{6}+3\times 9\times\sqrt{6}-21\times 2\times\sqrt{6}\\\\&=&-60\sqrt{6}+54\sqrt{6}+27\sqrt{6}-42\sqrt{6}\\\\&=&-21\sqrt{6}\end{array}$
Ainsi, $\boxed{D=-21\sqrt{6}}$
Soit $E=\sqrt{2}\sqrt{3}-\sqrt{54}+\sqrt{\dfrac{24}{49}}$
Alors, on a :
$\begin{array}{rcl} E&=&\sqrt{2}\sqrt{3}-\sqrt{54}+\sqrt{\dfrac{24}{49}}\\\\&=&\sqrt{2\times 3}-\sqrt{9\times 6}+\dfrac{\sqrt{24}}{\sqrt{49}}\\\\&=&\sqrt{6}-\sqrt{9}\times\sqrt{6}+\dfrac{\sqrt{4\times 6}}{7}\\\\&=&\sqrt{6}-3\times\sqrt{6}+\dfrac{\sqrt{4}\times\sqrt{6}}{7}\\\\&=&\sqrt{6}-3\sqrt{6}+\dfrac{2\sqrt{6}}{7}\\\\&=&\dfrac{7\sqrt{6}}{7}-\dfrac{21\sqrt{6}}{7}+\dfrac{2\sqrt{6}}{7}\\\\&=&\dfrac{7\sqrt{6}-21\sqrt{6}+2\sqrt{6}}{7}\\\\&=&-\dfrac{12}{7}\sqrt{6}\end{array}$
D'où, $\boxed{E=-\dfrac{12}{7}\sqrt{6}}$
Soit $F=\dfrac{7}{3}\sqrt{\dfrac{54}{16}}-\dfrac{6}{5}\sqrt{\dfrac{30}{20}}-\dfrac{9}{2}\sqrt{\dfrac{24}{81}}$
Alors, on a :
$\begin{array}{rcl} F&=&\dfrac{7}{3}\sqrt{\dfrac{54}{16}}-\dfrac{6}{5}\sqrt{\dfrac{30}{20}}-\dfrac{9}{2}\sqrt{\dfrac{24}{81}}\\\\&=&\dfrac{7}{3}\dfrac{\sqrt{54}}{\sqrt{16}}-\dfrac{6}{5}\dfrac{\sqrt{30}}{\sqrt{20}}-\dfrac{9}{2}\dfrac{\sqrt{24}}{\sqrt{81}}\\\\&=&\dfrac{7}{3}\dfrac{\sqrt{9\times 6}}{4}-\dfrac{6}{5}\dfrac{\sqrt{5\times 6}}{\sqrt{4\times 5}}-\dfrac{9}{2}\dfrac{\sqrt{4\times 6}}{9}\\\\&=&\dfrac{7}{3}\times\dfrac{\sqrt{9}\times\sqrt{6}}{4}-\dfrac{6}{5}\times\dfrac{\sqrt{5}\times\sqrt{6}}{\sqrt{4}\times\sqrt{5}}-\dfrac{9}{2}\times\dfrac{\sqrt{4}\times\sqrt{6}}{9}\\\\&=&\dfrac{7\times 3\times\sqrt{6}}{3\times 4}-\dfrac{6\times\sqrt{6}}{5\times 2}-\dfrac{9\times 2\times\sqrt{6}}{2\times 9}\\\\&=&\dfrac{7}{4}\sqrt{6}-\dfrac{3}{5}\sqrt{6}-\sqrt{6}\\\\&=&\dfrac{35}{20}\sqrt{6}-\dfrac{12}{20}\sqrt{6}-\dfrac{20}{20}\sqrt{6}\\\\&=&\dfrac{(35-12-20)}{20}\sqrt{6}\\\\&=&\dfrac{3}{20}\sqrt{6}\end{array}$
Donc, $\boxed{F=\dfrac{3}{20}\sqrt{6}}$
Exercice 8
1) Rendons rationnel le dénominateur des nombres suivants :
$$\dfrac{5-2\sqrt{3}}{3\sqrt{3}-5}\;,\quad\dfrac{3\sqrt{5}-3}{2\sqrt{3}}\;,\quad\dfrac{2}{3\sqrt{2}-2\sqrt{3}}$$
Soit le nombre $\dfrac{5-2\sqrt{3}}{3\sqrt{3}-5}$
Alors, l'expression conjuguée du dénominateur est égale à $3\sqrt{3}+5.$
Donc, pour rendre rationnel le nombre $\dfrac{5-2\sqrt{3}}{3\sqrt{3}-5}$, on multiplie son numérateur et son dénominateur par le même nombre $3\sqrt{3}+5.$
Ainsi, on a :
$\begin{array}{rcl}\dfrac{5-2\sqrt{3}}{3\sqrt{3}-5}&=&\dfrac{(5-2\sqrt{3})(3\sqrt{3}+5)}{(3\sqrt{3}-5)(3\sqrt{3}+5)}\\\\&=&\dfrac{15\sqrt{3}+25-(2\sqrt{3})\times(3\sqrt{3})-10\sqrt{3}}{(3\sqrt{3})^{2}-(5)^{2}}\\\\&=&\dfrac{15\sqrt{3}+25-18-10\sqrt{3}}{27-25}\\\\&=&\dfrac{5\sqrt{3}+7}{2}\end{array}$
D'où, $\boxed{\dfrac{5-2\sqrt{3}}{3\sqrt{3}-5}=\dfrac{5\sqrt{3}+7}{2}}$
Soit le nombre $\dfrac{3\sqrt{5}-3}{2\sqrt{3}}$
Alors, pour rendre rationnel ce nombre, on multiplie son numérateur et son dénominateur par le même nombre $\sqrt{3}.$
Donc, on a :
$\begin{array}{rcl}\dfrac{3\sqrt{5}-3}{2\sqrt{3}}&=&\dfrac{(3\sqrt{5}-3)\sqrt{3}}{2\sqrt{3}\times\sqrt{3}}\\\\&=&\dfrac{3\sqrt{5}\times\sqrt{3}-3\sqrt{3}}{2\times 3}\\\\&=&\dfrac{3\sqrt{5\times 3}-3\sqrt{3}}{6}\\\\&=&\dfrac{3\sqrt{15}-3\sqrt{3}}{6}\\\\&=&\dfrac{3(\sqrt{15}-\sqrt{3})}{6}\\\\&=&\dfrac{\sqrt{15}-\sqrt{3}}{2}\end{array}$
Ainsi, $\boxed{\dfrac{3\sqrt{5}-3}{2\sqrt{3}}=\dfrac{\sqrt{15}-\sqrt{3}}{2}}$
Soit le nombre $\dfrac{2}{3\sqrt{2}-2\sqrt{3}}$
Alors, l'expression conjuguée du dénominateur est égale à $3\sqrt{2}+2\sqrt{3}.$
Donc, pour rendre rationnel le nombre $\dfrac{2}{3\sqrt{2}-2\sqrt{3}}$, on multiplie son numérateur et son dénominateur par le même nombre $3\sqrt{2}+2\sqrt{3}.$
On obtient alors :
$\begin{array}{rcl}\dfrac{2}{3\sqrt{2}-2\sqrt{3}}&=&\dfrac{2(3\sqrt{2}+2\sqrt{3})}{(3\sqrt{2}-2\sqrt{3})(3\sqrt{2}+2\sqrt{3})}\\\\&=&\dfrac{2(3\sqrt{2}+2\sqrt{3})}{(3\sqrt{2})^{2}-(2\sqrt{3})^{2}}\\\\&=&\dfrac{2(3\sqrt{2}+2\sqrt{3})}{18-12}\\\\&=&\dfrac{2(3\sqrt{2}+2\sqrt{3})}{6}\\\\&=&\dfrac{3\sqrt{2}+2\sqrt{3}}{3}\end{array}$
D'où, $\boxed{\dfrac{2}{3\sqrt{2}-2\sqrt{3}}=\dfrac{3\sqrt{2}+2\sqrt{3}}{3}}$
2) Mettons les expressions suivantes sous la forme :
$$a+b\sqrt{c}\quad\text{ avec }a\in\mathbb{Q}\;,\ b\in\mathbb{Q}\text{ et }c\in\mathbb{N}$$
Soit $A=\dfrac{2}{1-\sqrt{3}}+\dfrac{1}{1+\sqrt{3}}$
Alors, en réduisant au même dénominateur, on obtient :
$\begin{array}{rcl} A&=&\dfrac{2}{1-\sqrt{3}}+\dfrac{1}{1+\sqrt{3}}\\\\&=&\dfrac{2(1+\sqrt{3})+1(1-\sqrt{3})}{(1-\sqrt{3})(1+\sqrt{3})}\\\\&=&\dfrac{2+2\sqrt{3}+1-\sqrt{3}}{(1)^{2}-(\sqrt{3})^{2}}\\\\&=&\dfrac{3+\sqrt{3}}{1-3}\\\\&=&\dfrac{3+\sqrt{3}}{-2}\\\\&=&-\dfrac{3+\sqrt{3}}{2}\end{array}$
D'où, $\boxed{A=-\dfrac{3+\sqrt{3}}{2}}$
Soit $B=\dfrac{\sqrt{3}}{\sqrt{3}-\sqrt{2}}+\dfrac{\sqrt{2}}{\sqrt{3}+\sqrt{2}}$
Alors, en réduisant au même dénominateur, on obtient :
$\begin{array}{rcl} B&=&\dfrac{\sqrt{3}}{\sqrt{3}-\sqrt{2}}+\dfrac{\sqrt{2}}{\sqrt{3}+\sqrt{2}}\\\\&=&\dfrac{\sqrt{3}(\sqrt{3}+\sqrt{2})+\sqrt{2}(\sqrt{3}-\sqrt{2})}{(\sqrt{3}-\sqrt{2})(\sqrt{3}+\sqrt{2})}\\\\&=&\dfrac{\sqrt{3}\times\sqrt{3}+\sqrt{3}\times\sqrt{2}+\sqrt{2}\times\sqrt{3}-\sqrt{2}\times\sqrt{2}}{(\sqrt{3})^{2}-(\sqrt{2})^{2}}\\\\&=&\dfrac{3+\sqrt{3\times 2}+\sqrt{2\times 3}-2}{3-2}\\\\&=&\dfrac{3+\sqrt{6}+\sqrt{6}-2}{1}\\\\&=&1+2\sqrt{6}\end{array}$
Ainsi, $\boxed{B=1+2\sqrt{6}}$
3) Donnons une écriture simplifiée de :
$\begin{array}{rcl} C&=&3\sqrt{\dfrac{1}{75}}\times 2\sqrt{\dfrac{3}{4}}\\\\&=&3\dfrac{\sqrt{1}}{\sqrt{75}} \times 2\dfrac{\sqrt{3}}{\sqrt{4}}\\\\&=&3\dfrac{1}{\sqrt{25\times 3}}\times 2\dfrac{\sqrt{3}}{2}\\\\&=&\dfrac{3}{\sqrt{25}\times\sqrt{3}}\times\sqrt{3}\\\\&=&\dfrac{3}{5}\end{array}$
Donc, $\boxed{C=\dfrac{3}{5}}$
$\begin{array}{rcl} D&=&\sqrt{\left(\dfrac{3}{2}\right)^{2}}+4\\\\&=&\left|\dfrac{3}{2}\right|+4\\\\&=&\dfrac{3}{2}+4\\\\&=&\dfrac{3+8}{2}\\\\&=&\dfrac{11}{2}\end{array}$
Alors, $\boxed{D=\dfrac{11}{2}}$
$\begin{array}{rcl} E&=&(1-\sqrt{2})(5\sqrt{2}+3)+(1-\sqrt{2})^{2}\\\\&=&(1-\sqrt{2})[(5\sqrt{2}+3)+(1-\sqrt{2})]\\\\&=&(1-\sqrt{2})(5\sqrt{2}+3+1-\sqrt{2})\\\\&=&(1-\sqrt{2})(4+4\sqrt{2})\\\\&=&(1-\sqrt{2})(1+\sqrt{2})\times 4\\\\&=&((1)^{2}-(\sqrt{2})^{2})\times 4\\\\&=&(1-2)\times 4\\\\&=&(-1)\times 4\\\\&=&-4\end{array}$
Donc, $\boxed{E=-4}$
$\begin{array}{rcl} F&=&\sqrt{\dfrac{1.6\times 2.5}{0.36}}\\\\&=&\sqrt{\dfrac{\dfrac{16}{10}\times\dfrac{25}{10}}{\dfrac{36}{100}}}\\\\&=&\sqrt{\dfrac{\dfrac{16\times 25}{100}}{\dfrac{36}{100}}}\\\\&=&\sqrt{\dfrac{16\times 25}{100}\times\dfrac{100}{36}}\\\\&=&\sqrt{\dfrac{16\times 25}{36}}\\\\&=&\dfrac{\sqrt{16\times 25}}{\sqrt{36}}\\\\&=&\dfrac{\sqrt{16}\times\sqrt{25}}{6}\\\\&=&\dfrac{4\times 5}{6}\\\\&=&\dfrac{20}{6}\\\\&=&\dfrac{10}{3}\end{array}$
Ainsi, $\boxed{F=\dfrac{10}{3}}$
4) Écrivons sans le grand radical.
Soit $F=\sqrt{(1-\sqrt{5})^{2}}=\left|1-\sqrt{5}\right|$
Alors, cherchons le signe de $(1-\sqrt{5}).$
Pour cela, comparons $1\ $ et $\ \sqrt{5}.$
On a : $1>0\ $ et $\ \sqrt{5}>0$
Alors, $1^{2}=1\ $ et $\ (\sqrt{5})^{2}=5$
Or, $5>1$ donc, $\sqrt{5}>1$
D'où, $(1-\sqrt{5})<0$
Par conséquent,
$\begin{array}{rcl} \left|1-\sqrt{5}\right|&=&-(1-\sqrt{5})\\\\&=&-1+\sqrt{5}\end{array}$
Ainsi, $\boxed{F=\sqrt{5}-1}$
Soit $G=\sqrt{(-5-\sqrt{3})^{2}}=|-5-\sqrt{3}|$
Or, on sait que $(-5-\sqrt{3})$ est négatif.
Donc,
$\begin{array}{rcl}\left|(-5-\sqrt{3})\right|&=&-(-5-\sqrt{3})\\\\&=&(5+\sqrt{3})\end{array}$
D'où, $\boxed{G=5+\sqrt{3}}$
Soit $H=\sqrt{(5-2\sqrt{3})^{2}}=\left|5-2\sqrt{3}\right|$
Cherchons alors le signe de $(5-2\sqrt{3})$
Pour cela, comparons $5\ $ et $\ 2\sqrt{3}.$
On a : $5>0\ $ et $\ 2\sqrt{3}>0$
Alors, $5^{2}=25\ $ et $\ (2\sqrt{3})^{2}=12$
Comme, $25$ est plus grand que $12$ alors, $5>2\sqrt{3}$
D'où, $(5-2\sqrt{3})>0$
Par conséquent, $\left|5-2\sqrt{3}\right|=5-2\sqrt{3}$
Ainsi, $\boxed{H=5-2\sqrt{3}}$
Soit : $I=\sqrt{(-2\sqrt{3}+4)^{2}}=\left|-2\sqrt{3}+4\right|$
Alors, cherchons le signe de $(4-2\sqrt{3})$
Pour cela, comparons $4\ $ et $\ 2\sqrt{3}.$
On a : $4>0\ $ et $\ 2\sqrt{3}>0$
Alors, $4^{2}=16\ $ et $\ (2\sqrt{3})^{2}=12$
Or, $16$ est plus grand que $12$ donc, $4>2\sqrt{3}$
D'où, $(4-2\sqrt{3})>0$
Par conséquent, $\left|-2\sqrt{3}+4\right|=-2\sqrt{3}+4$
Ainsi, $\boxed{I=4-2\sqrt{3}}$
Soit $J=\sqrt{\left(\dfrac{3}{2}-2\sqrt{2}\right)^{2}}=\left|\dfrac{3}{2}-2\sqrt{2}\right|$
Cherchons alors le signe de $\left(\dfrac{3}{2}-2\sqrt{2}\right)$
Pour cela, comparons $\dfrac{3}{2}\ $ et $\ 2\sqrt{2}.$
On a : $\dfrac{3}{2}>0\ $ et $\ 2\sqrt{2}>0$
Alors, $\left(\dfrac{3}{2}\right)^{2}=\dfrac{9}{4}\ $ et $\ (2\sqrt{2})^{2}=8$
Or, on sait que $\dfrac{9}{4}$ est plus petit que $8$ donc, $\dfrac{3}{2}<2\sqrt{2}$
D'où, $\left(\dfrac{3}{2}-2\sqrt{2}\right)<0$
Par conséquent,
$\begin{array}{rcl}\left|\dfrac{3}{2}-2\sqrt{2}\right|&=&-\left(\dfrac{3}{2}-2\sqrt{2}\right)\\\\&=&\left(-\dfrac{3}{2}+2\sqrt{2}\right)\end{array}$
Ainsi, $\boxed{J=2\sqrt{2}-\dfrac{3}{2}}$
Exercice 9
1) Écrivons $A=\sqrt{121}-2\sqrt{112}+\sqrt{63}-\sqrt{81}$ sous la forme $$p+q\sqrt{c}\quad(p\in\mathbb{Z}\;,\ q\in\mathbb{Z}\;,\ c\in\mathbb{N})$$
On sait que :
$121=11^{2}$
$81=9^{2}$
$112=16\times 7$
$63=9\times 7$
Donc, en remplaçant dans l'expression de $A$, on obtient :
$\begin{array}{rcl} A&=&\sqrt{121}-2\sqrt{112}+\sqrt{63}-\sqrt{81}\\\\&=&\sqrt{11^{2}}-2\sqrt{16\times 7}+\sqrt{9\times 7}-\sqrt{9^{2}}\\\\&=&11-2\sqrt{16}\times\sqrt{7}+\sqrt{9}\times\sqrt{7}-9\\\\&=&11-2\times 4\times\sqrt{7}+3\times\sqrt{7}-9\\\\&=&11-9-8\sqrt{7}+3\sqrt{7}\\\\&=&2-5\sqrt{7}\end{array}$
D'où, $\boxed{A=2-5\sqrt{7}}$
2) Soit l'expression $B(x)=x^{2}-1+(x+7)(2-2x).$
a) Développons, réduisons puis ordonnons $B(x).$
On a :
$\begin{array}{rcl} B(x)&=&x^{2}-1+(x+7)(2-2x)\\\\&=&x^{2}-1+x(2-2x)+7(2-2x)\\\\&=&x^{2}-1+2x-2x^{2}+14-14x\\\\&=&x^{2}-2x^{2}+2x-14x-1+14\\\\&=&-x^{2}-12x+13\end{array}$
Alors, $\boxed{B=-x^{2}-12x+13}$
b) Factorisons $B(x).$
En effet, la propriété des identités remarquables, on a :
$$x^{2}-1=(x-1)(x+1)$$
De plus, on peut écrire : $(2-2x)=2(1-x)$
Alors, en remplaçant ces égalités dans l'expression de $B$, on trouve :
$\begin{array}{rcl} B(x)&=&x^{2}-1+(x-7)(2-2x)\\\\&=&(x-1)(x+1)+2(x-7)(1-x)\\\\&=&(1-x)[(x+1)+2(x-7)]\\\\&=&(1-x)(x+1+2x-14)\\\\&=&(1-x)(3x-13)\end{array}$
D'où, $\boxed{B=(1-x)(3x-13)}$
3) Soit l'expression $q(x)=\dfrac{B(x)}{(x-1)(x+7)}$
a) Établissons la condition d'existence de $q(x)$ et la Simplifions.
On sait que le dénominateur d'un quotient doit être toujours différent de zéro $(0).$
Donc, $q(x)$ existe si, et seulement si, son dénominateur est différent de $0.$
Ce qui signifie que : $(x-1)(x+7)\neq 0$
Or, on a :
$\begin{array}{rcl} (x-1)(x+7)=0&\Leftrightarrow&x-1=0\ \text{ ou }\ x+7=0\\\\&\Leftrightarrow&x=1\ \text{ ou }\ x=-7\end{array}$
Ainsi, pour que le dénominateur soit non nul, il faut que $x\neq 1\ $ et $\ x\neq -7$
Par conséquent, $x$ différent de $1$ et de $-7$ est la condition d'existence de $q(x)$
$-\ $ Simplifions $q(x)$
On a : $q(x)=\dfrac{B(x)}{(x-1)(x+7)}$
Donc, remplaçons $B(x)$ par sa forme factorisée.
On obtient alors :
$\begin{array}{rcl} q(x)&=&\dfrac{B(x)}{(x-1)(x+7)}\\\\&=&\dfrac{(1-x)(3x-13)}{(x-1)(x+7)}\\\\&=&\dfrac{-(x-1)(3x-13)}{(x-1)(x+7)}\\\\&=&\dfrac{-(3x-13)}{x+7}\\\\&=&-\dfrac{3x-13}{x+7}\end{array}$
D'où, $\boxed{q(x)=-\dfrac{3x-13}{x+7}}$
b) Calculons $q(\sqrt{2})$ (sans radicale au dénominateur).
Pour cela, on utilise l'expression simplifiée de $q(x)$ pour calculer $q(\sqrt{2})$ puis de rendre rationnel le dénominateur.
On a :
$\begin{array}{rcl} q(\sqrt{2})&=&-\dfrac{3\sqrt{2}-13}{\sqrt{2}+7}\\\\&=&-\dfrac{(3\sqrt{2}-13)(\sqrt{2}-7)}{(\sqrt{2}+7)(\sqrt{2}-7)}\\\\&=&-\dfrac{3\sqrt{2}\times\sqrt{2}-7\times 3\sqrt{2}-13\sqrt{2}+7\times 13}{(\sqrt{2})^{2}-(7)^{2}}\\\\&=&-\dfrac{3\times 2-21\sqrt{2}-13\sqrt{2}+91}{2-49}\\\\&=&-\dfrac{6-34\sqrt{2}+91}{-47}\\\\&=&\dfrac{97-34\sqrt{2}}{47}\end{array}$
Ainsi, $\boxed{q(\sqrt{2})=\dfrac{97-34\sqrt{2}}{47}}$
c) Donnons un encadrement de $q(\sqrt{2})$ d'amplitude $0.1$ prés sachant que $1.41<\sqrt{2}<1.42$
On a : $1.41<\sqrt{2}<1.42$
Alors, on multiplie chaque membre de l'inégalité par $-34$ tout en sachant que les inégalités changent de sens lorsqu'on multiplie par un même nombre négatif.
On obtient :
$$-34\times 1.41>-34\sqrt{2}>-34\times 1.42$$
Ce qui donne : $-47.94>-34\sqrt{2}>-48.28$
En ajoutant $97$ à chaque membre, on obtient :
$$97-47.94>97-34\sqrt{2}>97-48.28$$
C'est-à-dire ; $49.06>97-34\sqrt{2}>48.72$
On divise chaque membre de l'inégalité par le même nombre $47.$
On trouve alors :
$$\dfrac{49.06}{47}>\dfrac{97-34\sqrt{2}}{47}>\dfrac{48.72}{47}$$
Ce qui donne : $1.04>\dfrac{97-34\sqrt{2}}{47}>1.03$
Ou encore : $1.03<\dfrac{97-34\sqrt{2}}{47}<1.04$
D'où, un encadrement de $q(\sqrt{2})$ d'amplitude $0.1$ prés est donné par :
$$\boxed{1.0<\dfrac{97-34\sqrt{2}}{47}<1.1}$$
Exercice 10
On donne $A=\dfrac{\dfrac{4}{-\sqrt{5}-2}}{\dfrac{1}{2-\sqrt{5}}}\ $ et $\ B=4-2\sqrt{5}$
1) Écrivons $A\ $ et $\ B^{2}$ sous la forme $x+y\sqrt{5}.$
On a :
$\begin{array}{rcl} A&=&\dfrac{\dfrac{4}{-\sqrt{5}-2}}{\dfrac{1}{2-\sqrt{5}}}\\\\&=&\dfrac{4}{-\sqrt{5}-2}\times\dfrac{2-\sqrt{5}}{1}\\\\&=&\dfrac{4(2-\sqrt{5})}{-\sqrt{5}-2}\\\\&=&\dfrac{4(2-\sqrt{5})(-\sqrt{5}+2)}{(-\sqrt{5}-2)(-\sqrt{5}+2)}\\\\&=&\dfrac{4(-2\sqrt{5}+4-\sqrt{5}\times(-\sqrt{5})-2\sqrt{5})}{(-\sqrt{5})^{2}-(2)^{2}}\\\\&=&\dfrac{4(-4\sqrt{5}+4+5)}{5-4}\\\\&=&\dfrac{4(-4\sqrt{5}+9)}{1}\\\\&=&36-16\sqrt{5}\end{array}$
Donc, $\boxed{A=36-16\sqrt{5}}$
Soit $B=4-2\sqrt{5}$
Alors, $B^{2}$ est donné par :
$\begin{array}{rcl} B^{2}&=&(4-2\sqrt{5})^{2}\\\\&=&4^{2}-2\times 4\times 2\sqrt{5}+(2\sqrt{5})^{2}\\\\&=&16-16\sqrt{5}+4\times 5\\\\&=&16-16\sqrt{5}+20\\\\&=&36-16\sqrt{5}\end{array}$
D'où, $\boxed{B^{2}=36-16\sqrt{5}}$
En déduisons une écriture simplifiée de $C=\sqrt{A}.$
Soit $C=\sqrt{A}=\sqrt{36-16\sqrt{5}}$
Or, on sait que $36-16\sqrt{5}=B^{2}$
Donc, en remplaçant $36-16\sqrt{5}$ par $B^{2}$, on obtient :
$\begin{array}{rcl} C&=&\sqrt{36-16\sqrt{5}}\\\\&=&\sqrt{B^{2}}\\\\&=&|B|\end{array}$
Donc, $C=|B|$
Cherchons alors le signe de $B$
Pour cela, comparons $4\ $ et $\ 2\sqrt{5}$
On a : $4>0\ $ et $\ 2\sqrt{5}>0$
Alors, $4^{2}=16\ $ et $\ (2\sqrt{5})^{2}=20$
Comme $20$ est plus grand que $16$ alors, $4<2\sqrt{5}$
D'où, $4-2\sqrt{5}<0$
Ce qui signifie que $B$ est négatif.
Par suite, $|B|=-B$
Ainsi,
$\begin{array}{rcl} C&=&|B|\\\\&=&-B\\\\&=&-(4-2\sqrt{5})\\\\&=&-4+2\sqrt{5}\end{array}$
D'où, $\boxed{C=-4+2\sqrt{5}}$
2) Sachant que $2.23<\sqrt{5}<2.24$ ; donnons un encadrement de $B\ $ et $\ C$ à $10^{-1}$ près.
$-\ $ Encadrement de $B$
On a : $2.23<\sqrt{5}<2.24$
Alors, on multiplie chaque membre de l'inégalité par $-2$ tout en sachant que les inégalités changent de sens lorsqu'on multiplie par un même nombre négatif.
On obtient :
$$-2\times 2.23>-2\sqrt{5}>-2\times 2.24$$
Ce qui donne : $-4.46>-2\sqrt{5}>-4.48$
En ajoutant $4$ à chaque membre, on obtient :
$$4-4.46>4-2\sqrt{5}>4-4.48$$
Ce qui donne : $-0.46>4-2\sqrt{5}>-0.48$
D'où, un encadrement de $B$ à $10^{-1}$ prés est donné par :
$$\boxed{-0.5<4-2\sqrt{5}<-0.4}$$
$-\ $ Encadrement de $C$
Comme $C=-B$ alors, pour obtenir un encadrement de $C$, il suffit de multiplier chaque membre de l'encadrement de $B$ par $-1$ en changeant le sens des inégalités.
On obtient alors :
$$-1\times(-0.5)>-(4-2\sqrt{5})>-1\times(-0.4)$$
Ce qui donne : $0.5>-4+2\sqrt{5}>0.4$
D'où, un encadrement de $C$ à $10^{-1}$ prés est donné par :
$$\boxed{0.4<-4+2\sqrt{5}<0.5}$$
Exercice 11
On donne $a=\dfrac{-6}{2\sqrt{3}-3\sqrt{2}}\ $ et $\ b=4-2\sqrt{3}$
1) Écrivons $a$ sous la forme $x\sqrt{3}+y\sqrt{2}$ puis, calculons $a^{2}.$
En rendant rationnel le dénominateur de $a$, on obtient :
$\begin{array}{rcl} a&=&\dfrac{-6}{2\sqrt{3}-3\sqrt{2}}\\\\&=&\dfrac{-6(2\sqrt{3}+3\sqrt{2})}{(2\sqrt{3}-3\sqrt{2})(2\sqrt{3}+3\sqrt{2})}\\\\&=&\dfrac{-6(2\sqrt{3}+3\sqrt{2})}{(2\sqrt{3})^{2}-(3\sqrt{2})^{2}}\\\\&=&\dfrac{-6(2\sqrt{3}+3\sqrt{2})}{(4\times 3)-(9\times 2)}\\\\&=&\dfrac{-6(2\sqrt{3}+3\sqrt{2})}{12-18}\\\\&=&\dfrac{-6(2\sqrt{3}+3\sqrt{2})}{-6}\\\\&=&2\sqrt{3}+3\sqrt{2}\end{array}$
D'où, $\boxed{a=2\sqrt{3}+3\sqrt{2}}$
$\ $ Calcul de $a^{2}$
Comme $a$ peut encore s'écrire $a=2\sqrt{3}+3\sqrt{2}$ alors, utilisons cette nouvelle écriture de $a$ pour calculer $a^{2}.$
On a alors :
$\begin{array}{rcl} a^{2}&=&(2\sqrt{3}+3\sqrt{2})^{2}\\\\&=&(2\sqrt{3})^{2}+2\times(2\sqrt{3})\times(3\sqrt{2})+(3\sqrt{2})^{2}\\\\&=&(4\times 3)+2\times 2\times 3\times\sqrt{3}\times\sqrt{2}+(9\times 2)\\\\&=&12+12\sqrt{3\times 2}+18\\\\&=&30+12\sqrt{6}\end{array}$
Ainsi, $\boxed{a^{2}=30+12\sqrt{6}}$
En déduisons une écriture simplifiée de $C=\dfrac{30+12\sqrt{6}}{2\sqrt{3}-3\sqrt{2}}.$
On sait que $30+12\sqrt{6}=a^{2}$
De plus, on a : $a=\dfrac{-6}{2\sqrt{3}-3\sqrt{2}}$
Donc, $a\times(2\sqrt{3}-3\sqrt{2})=-6$
Ce qui donne : $2\sqrt{3}-3\sqrt{2}=\dfrac{-6}{a}$
Ainsi, dans l'expression de $C$, en remplaçant $30+12\sqrt{6}$ par $a^{2}\ $ et $2\sqrt{3}-3\sqrt{2}$ par $\dfrac{-6}{a}$, on obtient :
$\begin{array}{rcl} C&=&\dfrac{30+12\sqrt{6}}{2\sqrt{3}-3\sqrt{2}}\\\\&=&\dfrac{a^{2}}{\dfrac{-6}{a}}\\\\&=&\dfrac{a^{2}}{1}\times\dfrac{a}{-6}\\\\&=&\dfrac{a^{2}\times a}{-6}\\\\&=&-\dfrac{a^{3}}{6}\end{array}$
D'où, $\boxed{C=-\dfrac{a^{3}}{6}}$
2) Calculons $b^{2}$ puis, montrons que $d=\dfrac{12-3\sqrt{12}}{\sqrt{28-16\sqrt{3}}}\in\mathbb{N}$
Soit $b=4-2\sqrt{3}$
Alors, $b^{2}$ est donné par :
$\begin{array}{rcl} b^{2}&=&(4-2\sqrt{3})^{2}\\\\&=&4^{2}-2\times 4\times 2\sqrt{3}+(2\sqrt{3})^{2}\\\\&=&16-16\sqrt{3}+4\times 3\\\\&=&16-16\sqrt{3}+12\\\\&=&28-16\sqrt{3}\end{array}$
D'où, $\boxed{b^{2}=28-16\sqrt{3}}$
Montrons que $d=\dfrac{12-3\sqrt{12}}{\sqrt{28-16\sqrt{3}}}\in\mathbb{N}$
Pour cela, on montre que $d$ est un entier naturel.
En effet, le numérateur de $d$, peut encore s'écrire :
$\begin{array}{rcl} 12-3\sqrt{12}&=&12-3\sqrt{4\times 3}\\\\&=&12-3\sqrt{4}\times\sqrt{3}\\\\&=&12-3\times 2\times\sqrt{3}\\\\&=&12-6\sqrt{3}\end{array}$
Donc, $12-3\sqrt{12}=12-6\sqrt{3}$
Aussi, comme $b^{2}=28-16\sqrt{3}$ alors, le dénominateur de $d$ s'écrit :
$$\sqrt{28-16\sqrt{3}}=\sqrt{b^{2}}=|b|$$
Cherchons alors le signe de $b$
Pour cela, comparons $4\ $ et $\ 2\sqrt{3}$
On a : $4>0\ $ et $\ 2\sqrt{3}>0$
Alors, $4^{2}=16\ $ et $\ (2\sqrt{3})^{2}=12$
Comme $16$ est plus grand que $12$ alors, $4>2\sqrt{3}$
D'où, $4-2\sqrt{3}>0$
Ce qui signifie que $b$ est positif.
Par suite, $|b|=b=4-2\sqrt{3}$
Ainsi, $\sqrt{28-16\sqrt{3}}=4-2\sqrt{3}$
Donc, dans l'écriture de $d$, en remplaçant le numérateur par $12-6\sqrt{3}$ et le dénominateur par $4-2\sqrt{3}$, on obtient :
$\begin{array}{rcl} d&=&\dfrac{12-3\sqrt{12}}{\sqrt{28-16\sqrt{3}}}\\\\&=&\dfrac{12-6\sqrt{3}}{4-2\sqrt{3}}\\\\&=&\dfrac{3(4-2\sqrt{3})}{4-2\sqrt{3}}\\\\&=&3\end{array}$
D'où, $\boxed{d=3\quad\text{qui est bien un entier naturel}}$
Exercice 12
1) Écrivons sous la forme $a\sqrt{b}$ où $a\ $ et $\ b$ sont des entiers : $\sqrt{45}\;;\ \sqrt{12}\;;\ \sqrt{20}.$
On sait que : $45=9\times 5$
Donc, en remplaçant, on trouve :
$\begin{array}{rcl} \sqrt{45}&=&\sqrt{9\times 5}\\\\&=&\sqrt{9}\times\sqrt{5}\\\\&=&3\times\sqrt{5}\\\\&=&3\sqrt{5}\end{array}$
D'où, $\boxed{\sqrt{45}=3\sqrt{5}}$
On a : $12=4\times 3$
Donc, en remplaçant, on obtient :
$\begin{array}{rcl} \sqrt{12}&=&\sqrt{4\times 3}\\\\&=&\sqrt{4}\times\sqrt{3}\\\\&=&2\times\sqrt{3}\\\\&=&2\sqrt{3}\end{array}$
Ainsi, $\boxed{\sqrt{12}=2\sqrt{3}}$
On sait que : $20=4\times 5$
Donc, en remplaçant, on trouve :
$\begin{array}{rcl} \sqrt{20}&=&\sqrt{4\times 5}\\\\&=&\sqrt{4}\times\sqrt{5}\\\\&=&2\times\sqrt{5}\\\\&=&2\sqrt{5}\end{array}$
D'où, $\boxed{\sqrt{20}=2\sqrt{5}}$
2) Écrivons $C=\sqrt{45}+\sqrt{12}+\sqrt{20}-2\sqrt{3}$ sous la forme $d\sqrt{5}$ où $d$ est un entier.
En remplaçant $\sqrt{45}\;;\ \sqrt{12}\;;\ \sqrt{20}$ par leur écriture plus simplifiée, on obtient :
$\begin{array}{rcl} C&=&\sqrt{45}+\sqrt{12}+\sqrt{20}-2\sqrt{3}\\\\&=&3\sqrt{5}+2\sqrt{3}+2\sqrt{5}-2\sqrt{3}\\\\&=&5\sqrt{5}\end{array}$
D'où, $\boxed{C=5\sqrt{5}}$
3) Montrons que $E=(1+\sqrt{2})^{2}-(\sqrt{8}-1)$ est un entier.
En calculant directement, on obtient :
$\begin{array}{rcl} E&=&(1+\sqrt{2})^{2}-(\sqrt{8}-1)\\\\&=&1^{2}+2\times 1\times\sqrt{2}+(\sqrt{2})^{2}-\sqrt{8}+1\\\\&=&1+2\sqrt{2}+2-\sqrt{4\times 2}+1\\\\&=&4+2\sqrt{2}-\sqrt{4}\times\sqrt{2}\\\\&=&4+2\sqrt{2}-2\sqrt{2}\\\\&=&4\end{array}$
D'où, $\boxed{E=4\quad\text{qui est un entier naturel}}$
Exercice 13
On donne : $a=\sqrt{10}-3\ $ et $\ b=\sqrt{\dfrac{\sqrt{10}-3}{\sqrt{10}+3}}$
1) Calculons $a^{2}$ puis rendons rationnel le dénominateur de $\dfrac{\sqrt{10}-3}{\sqrt{10}+3}$
On a :
$\begin{array}{rcl} a^{2}&=&(\sqrt{10}-3)^{2}\\\\&=&(\sqrt{10})^{2}-2\times 3\times\sqrt{10}+(3)^{2}\\\\&=&10-6\sqrt{10}+9\\\\&=&19-6\sqrt{10}\end{array}$
Donc, $\boxed{a^{2}=19-6\sqrt{10}}$
Rendons rationnel le dénominateur de $\dfrac{\sqrt{10}-3}{\sqrt{10}+3}$
On a :
$\begin{array}{rcl} \dfrac{\sqrt{10}-3}{\sqrt{10}+3}&=&\dfrac{(\sqrt{10}-3)(\sqrt{10}-3)}{(\sqrt{10}+3)(\sqrt{10}-3)}\\\\&=&\dfrac{(\sqrt{10}-3)^{2}}{(\sqrt{10})^{2}-(3)^{2}}\\\\&=&\dfrac{19-6\sqrt{10}}{10-9}\\\\&=&\dfrac{19-6\sqrt{10}}{1}\\\\&=&19-6\sqrt{10}\end{array}$
Ainsi, $\boxed{\dfrac{\sqrt{10}-3}{\sqrt{10}+3}=19-6\sqrt{10}}$
On peut remarquer que $\dfrac{\sqrt{10}-3}{\sqrt{10}+3}=a^{2}$
2) Simplifions l'écriture de $b$.
Soit $b=\sqrt{\dfrac{\sqrt{10}-3}{\sqrt{10}+3}}$
Comme $\dfrac{\sqrt{10}-3}{\sqrt{10}+3}=a^{2}$ alors, on a :
$\begin{array}{rcl} \sqrt{\dfrac{\sqrt{10}-3}{\sqrt{10}+3}}&=&\sqrt{a^{2}}\\\\&=&|a|\end{array}$
Donc, $\boxed{b=|a|}$
Déterminons alors le signe de $a=\sqrt{10}-3$
Pour cela, comparons $\sqrt{10}\ $ et $\ 3$
On a : $\sqrt{10}>0\ $ et $\ 3>0$
Alors, $(\sqrt{10})^{2}=10\ $ et $\ (3)^{2}=9$
Comme $10$ est plus grand que $9$ alors, $\sqrt{10}>3$
D'où, $\sqrt{10}-3>0$
Ce qui signifie que $a$ est positif.
Par suite, $|a|=a=\sqrt{10}-3$
Or, $b=|a|$
Par conséquent, $\boxed{b=\sqrt{10}-3}$
3) Sachant que $3.162<\sqrt{10}<3.163$ ; donnons un encadrement de $3-\sqrt{10}$ au dixième près.
On a : $3.162<\sqrt{10}<3.163$
Alors, on multiplie chaque membre de l'inégalité par $-1$ en changeant le sens des inégalités.
On obtient :
$-3.162>-\sqrt{10}>-3.163$
Ensuite, en ajoutant $3$ à chaque membre, on trouve :
$3-3.162>3-\sqrt{10}>3-3.163$
Ce qui donne : $-0.162>3-\sqrt{10}>-0.163$
Ce qui s'écrit encore : $-0.163<3-\sqrt{10}<-0.162$
D'où, un encadrement de $3-\sqrt{10}$ au dixième prés est donné par :
$$\boxed{-0.2<3-\sqrt{10}<-0.1}$$
Exercice 14
Soient les réels $x\ $ et $\ y$ tels que :
$$x=\dfrac{2+\sqrt{3}}{2-\sqrt{3}}+\dfrac{2-\sqrt{3}}{2+\sqrt{3}}\;;\quad y=\sqrt{50}-\sqrt{32}-\sqrt{18}$$
1) Montrons que $x$ est un entier que l'on précisera.
Pour cela, on commence par réduire au même dénominateur puis, on calcule $x.$
On a :
$\begin{array}{rcl} x&=&\dfrac{2+\sqrt{3}}{2-\sqrt{3}}+\dfrac{2-\sqrt{3}}{2+\sqrt{3}}\\\\&=&\dfrac{(2+\sqrt{3})(2+\sqrt{3})}{(2-\sqrt{3})(2+\sqrt{3})}+\dfrac{(2-\sqrt{3})(2-\sqrt{3})}{(2+\sqrt{3})(2-\sqrt{3})}\\\\&=&\dfrac{(2+\sqrt{3})^{2}+(2-\sqrt{3})^{2}}{(2)^{2}-(\sqrt{3})^{2}}\\\\&=&\dfrac{(2)^{2}+2\times 2\times\sqrt{3}+(\sqrt{3})^{2}+(2)^{2}-2\times 2\times\sqrt{3}+(\sqrt{3})^{2}}{4-3}\\\\&=&\dfrac{4+4\sqrt{3}+3+4-4\sqrt{3}+3}{1}\\\\&=&14\end{array}$
Ainsi, $\boxed{x=14}$
Par conséquent $x$ est un entier.
2) Écrivons $y$ sous la forme $a\sqrt{b}$ avec $b$ un entier naturel.
Soit $y=\sqrt{50}-\sqrt{32}-\sqrt{18}$
Alors, on a :
$\begin{array}{rcl} y&=&\sqrt{50}-\sqrt{32}-\sqrt{18}\\\\&=&\sqrt{25\times 2}-\sqrt{16\times 2}-\sqrt{9\times 2}\\\\&=&\sqrt{25}\times\sqrt{2}-\sqrt{16}\times\sqrt{2}-\sqrt{9}\times\sqrt{2}\\\\&=&5\times\sqrt{2}-4\times\sqrt{2}-3\times\sqrt{2}\\\\&=&-2\sqrt{2}\end{array}$
D'où, $\boxed{y=-2\sqrt{2}}$
3) Donnons un encadrement de $x-y$ à $10^{-2}$ près.
On a :
$\begin{array}{rcl} x-y&=&14-(-2\sqrt{2})\\\\&=&14+2\sqrt{2}\end{array}$
On va alors donner un encadrement de $14+2\sqrt{2}$ à $10^{-2}$ près.
On sait que : $1.414<\sqrt{2}<1.415$
Alors, on multiplie chaque membre de l'inégalité par $2.$
On obtient :
$$2\times 1.414<2\sqrt{2}<2\times 1.415$$
Ce qui donne : $2.828<2\sqrt{2}<2.830$
En ajoutant $14$ à chaque membre, on trouve :
$$14+2.828<14+2\sqrt{2}<14+2.830$$
C'est-à-dire ; $16.828<14+2\sqrt{2}<16.830$
D'où, un encadrement de $x-y$ à $10^{-2}$ près est donné par :
$$\boxed{16.82<x-y<16.83}$$
Exercice 15
1) Simplifions les réels suivants :
Soit $A=-\sqrt{49}3+\sqrt{12}-\sqrt{(-5)^{2}}$
Alors, on a :
$\begin{array}{rcl} A&=&-\sqrt{49}3+\sqrt{12}-\sqrt{(-5)^{2}}\\\\&=&-\sqrt{49}\times 3+\sqrt{4\times 3}-|-5|\\\\&=&-7\times 3+\sqrt{4}\times\sqrt{3}-5\\\\&=&-21+2\sqrt{3}-5\\\\&=&-26+2\sqrt{3}\end{array}$
D'où, $\boxed{A=-26+2\sqrt{2}}$
Soit $B=\sqrt{12}+\sqrt{32}-\sqrt{144}-\sqrt{2}$
Alors, on a :
$\begin{array}{rcl} B&=&\sqrt{12}+\sqrt{32}-\sqrt{144}-\sqrt{2}\\\\&=&\sqrt{4\times 3}+\sqrt{16\times 2}-12-\sqrt{2}\\\\&=&\sqrt{4}\times\sqrt{3}+\sqrt{16}\times\sqrt{2}-12-\sqrt{2}\\\\&=&2\sqrt{3}+4\sqrt{2}-12-\sqrt{2}\\\\&=&-12+3\sqrt{2}+2\sqrt{3}\end{array}$
Ainsi, $\boxed{B=-12+3\sqrt{2}+2\sqrt{3}}$
Soit $C=3\sqrt{a^{4}}+a\sqrt{a^{2}}-5a^{2}$ avec $a\in\mathbb{R}^{-}$
Alors, on a :
$\begin{array}{rcl} C&=&3\sqrt{a^{4}}+a\sqrt{a^{2}}-5a^{2}\\\\&=&3\sqrt{a^{2}\times a^{2}}+a\times|a|-5a^{2}\\\\&=&3\sqrt{a^{2}}\times\sqrt{a^{2}}+a\times|a|-5a^{2}\\\\&=&3\times|a|\times|a|+a\times|a|-5a^{2}\end{array}$
Comme $a$ est un nombre négatif alors, $|a|=-a$
Donc, en remplaçant $|a|$ par $-a$, on trouve :
$\begin{array}{rcl} C&=&3\times|a|\times|a|+a\times|a|-5a^{2}\\\\&=&3\times(-a)\times(-a)+a\times(-a)-5a^{2}\\\\&=&3a^{2}-a^{2}-5a^{2}\\\\&=&-3a^{2}\end{array}$
D'où, $\boxed{C=-3a^{2}}$
2) Comparons les réels
$$-2\sqrt{5}\ \text{ et }\ -3\sqrt{5}$$
On remarque les nombres réels $-2\sqrt{5}\ $ et $\ -3\sqrt{5}$ sont tous les deux négatifs.
Donc, le plus grand est celui avec le plus petit carré.
On a : $(-2\sqrt{5})^{2}=20\ $ et $\ (-3\sqrt{5})^{2}=45$
Comme $20$ est plus petit que $45$ alors, $-2\sqrt{5}>-3\sqrt{5}$
$$3-2\sqrt{2}\ \text{ et }\ -1+\sqrt{2}$$
En faisant la différence entre ces deux nombres, on trouve :
$\begin{array}{rcl} (3-2\sqrt{2})-(-1+\sqrt{2})&=&3-2\sqrt{2}+1-\sqrt{2}\\\\&=&4-3\sqrt{2}\end{array}$
Donc, cette différence est égale à $4-3\sqrt{2}.$
Cherchons alors le signe de $4-3\sqrt{2}.$
On a : $4>0\ $ et $\ 3\sqrt{2}>0$
Alors, $(4)^{2}=16\ $ et $\ (3\sqrt{2})^{2}=18$
Comme $16$ est plus petit que $18$ alors, $4<3\sqrt{2}.$
D'où, $4-3\sqrt{2}<0$
Ce qui signifie que la différence $(3-2\sqrt{2})-(-1+\sqrt{2})$ est négative.
Par conséquent, $(3-2\sqrt{2})$ est inférieur à $(-1+\sqrt{2})$
$$\sqrt{5-2\sqrt{3}}\ \text{ et }\ \sqrt{3-\sqrt{3}}$$
Ces deux nombres sont positifs donc, comparons leur carré.
On a : $\left(\sqrt{5-2\sqrt{3}}\right)^{2}=5-2\sqrt{3}\ $ et $\ \left(\sqrt{3-\sqrt{3}}\right)^{2}=3-\sqrt{3}$
Alors, en faisant la différence entre les carrés de ces deux nombres, on obtient :
$\begin{array}{rcl} \left(\sqrt{5-2\sqrt{3}}\right)^{2}-\left(\sqrt{3-\sqrt{3}}\right)^{2}&=&(5-2\sqrt{3})-(3-\sqrt{3})\\\\&=&5-2\sqrt{3}-3+\sqrt{3}\\\\&=&2-\sqrt{3}\end{array}$
Donc, cette différence est égale à $2-\sqrt{3}.$
Cherchons alors le signe de $2-\sqrt{3}.$
On a : $2>0\ $ et $\ \sqrt{3}>0$
Alors, $(2)^{2}=4\ $ et $\ (\sqrt{3})^{2}=3$
Comme $4$ est plus grand que $3$ alors, $2>\sqrt{3}.$
D'où, $2-\sqrt{3}>0$
Ce qui signifie que la différence $\left(\sqrt{5-2\sqrt{3}}\right)^{2}-\left(\sqrt{3-\sqrt{3}}\right)^{2}$ est positive.
Ainsi, $\left(\sqrt{5-2\sqrt{3}}\right)^{2}$ est plus grand que $\left(\sqrt{3-\sqrt{3}}\right)^{2}$
Par conséquent, $\sqrt{5-2\sqrt{3}}>\sqrt{3-\sqrt{3}}$
Exercice 16
1) On donne $a=2+\sqrt{5}\ $ et $\ b=2-\sqrt{5}.$ Calculons $a^{2}\ $ et $\ b^{2}$ puis en déduisons une écriture simplifiée de $A=\sqrt{9+4\sqrt{5}}+\sqrt{9-4\sqrt{5}}.$
On a :
$\begin{array}{rcl} a^{2}&=&(2+\sqrt{5})^{2}\\\\&=&(2)^{2}+2\times 2\times\sqrt{5}+(\sqrt{5})^{2}\\\\&=&4+4\sqrt{5}+5\\\\&=&9+4\sqrt{5}\end{array}$
Donc, $\boxed{a^{2}=9+4\sqrt{5}}$
On a :
$\begin{array}{rcl} b^{2}&=&(2-\sqrt{5})^{2}\\\\&=&(2)^{2}-2\times 2\times\sqrt{5}+(\sqrt{5})^{2}\\\\&=&4-4\sqrt{5}+5\\\\&=&9-4\sqrt{5}\end{array}$
Donc, $\boxed{b^{2}=9-4\sqrt{5}}$
Simplifions l'écriture de $A=\sqrt{9+4\sqrt{5}}+\sqrt{9-4\sqrt{5}}.$
Comme $9+4\sqrt{5}=a^{2}\ $ et $9-4\sqrt{5}=b^{2}$ alors, $A$ peut encore s'écrire :
$\begin{array}{rcl} A&=&\sqrt{a^{2}}+\sqrt{b^{2}}\\\\&=&|a|+|b|\end{array}$
Cherchons alors le signe de $a\ $ et $\ b$
Soit $a=2+\sqrt{5}>0$ donc, $|a|=a$
Soit $b=2-\sqrt{5}$
On a : $2>0\ $ et $\ \sqrt{5}>0$
Alors, $(2)^{2}=4\ $ et $\ (\sqrt{5})^{2}=5$
Comme $4$ est plus petit que $5$ alors, $2<\sqrt{5}.$
D'où, $2-\sqrt{5}<0$
C'est-à-dire ; $b$ est négatif.
Par conséquent, $|b|=-b$
Donc,
$\begin{array}{rcl} A&=&|a|+|b|\\\\&=&a-b\\\\&=&(2+\sqrt{5})-(2-\sqrt{5})\\\\&=&2+\sqrt{5}-2+\sqrt{5}\\\\&=&2\sqrt{5}\end{array}$
D'où, $\boxed{A=2\sqrt{5}}$
2) On donne : $X=\sqrt{3+2\sqrt{2}}\ $ et $\ Y=\sqrt{3-2\sqrt{2}}$
a) Calculons $X.Y$
On a :
$\begin{array}{rcl} X\times Y&=&\sqrt{3+2\sqrt{2}}\times \sqrt{3-2\sqrt{2}}\\\\&=&\sqrt{(3+2\sqrt{2})\times(3-2\sqrt{2})}\\\\&=&\sqrt{(3)^{2}-(2\sqrt{2})^{2}}\\\\&=&\sqrt{9-8}\\\\&=&\sqrt{1}\\\\&=&1\end{array}$
Donc, $\boxed{X\times Y=1}$
On peut alors dire que $X\ $ et $\ Y$ sont des inverses.
b) On pose $M=X-Y$ ; calculons $M^{2}$ puis en déduisons que $M=2.$
On a :
$\begin{array}{rcl} M^{2}&=&(X-Y)^{2}\\\\&=&X^{2}-2\times X\times Y+Y^{2}\\\\&=&\left(\sqrt{3+2\sqrt{2}}\right)^{2}-2\times 1+\left(\sqrt{3-2\sqrt{2}}\right)^{2}\\\\&=&3+2\sqrt{2}-2+3-2\sqrt{2}\\\\&=&3+2\sqrt{2}-2+3-2\sqrt{2}\\\\&=&4\end{array}$
Donc, $\boxed{M^{2}=4}$
En déduisons que $M=2.$
On a : $M^{2}=4$
Alors, $\sqrt{M^{2}}=\sqrt{4}=2$
Or, $\sqrt{M^{2}}=|M|$ donc, $|M|=2$
Cherchons alors le signe de $M.$
On a : $M=X-Y=\sqrt{3+2\sqrt{2}}-\sqrt{3-2\sqrt{2}}$
Donc, comparons $\sqrt{3+2\sqrt{2}}\ $ et $\ \sqrt{3-2\sqrt{2}}$
Ces deux nombres étant positifs alors, on a :
$\left(\sqrt{3+2\sqrt{2}}\right)^{2}=3+2\sqrt{2}$
$\left(\sqrt{3-2\sqrt{2}}\right)^{2}=3-2\sqrt{2}$
En faisant la différence entre les carrés de ces deux nombres, on obtient :
$\begin{array}{rcl} \left(\sqrt{3+2\sqrt{2}}\right)^{2}-\left(\sqrt{3-2\sqrt{2}}\right)^{2}&=&3+2\sqrt{2}-(3-2\sqrt{2})\\\\&=&3+2\sqrt{2}-3+2\sqrt{2}\\\\&=&4\sqrt{2}\end{array}$
Donc, la différence $4\sqrt{2}$ est positive.
Ce qui signifie que $\left(\sqrt{3+2\sqrt{2}}\right)^{2}$ est supérieur à $\left(\sqrt{3-2\sqrt{2}}\right)^{2}$
Ainsi, $X$ est plus grand que $Y.$
Par suite, $M>0$
D'où, $|M|=M$
Or, on a $|M|=2$
Par conséquent, $\boxed{M=2}$
Exercice 17
1) On donne : $C=\sqrt{5\sqrt{2}-7}\ $ et $\ D=\sqrt{5\sqrt{2}+7}.$
Montrons que $C\ $ et $\ D$ sont inverses.
Pour cela, on va vérifier que $C\times D=1$
On a :
$\begin{array}{rcl} C\times D&=&\sqrt{5\sqrt{2}-7}\times\sqrt{5\sqrt{2}+7}\\\\&=&\sqrt{(5\sqrt{2}-7)\times(5\sqrt{2}+7)}\\\\&=&\sqrt{(5\sqrt{2})^{2}-(7)^{2}}\\\\&=&\sqrt{50-49}\\\\&=&\sqrt{1}\\\\&=&1\end{array}$
Donc, $\boxed{C\times D=1}$
Ce qui montre que $C\ $ et $\ D$ sont inverses.
2) Soit $E=\dfrac{3\sqrt{2}-1}{\sqrt{2}}.$
Rendons rationnel le dénominateur de $E.$
On a :
$\begin{array}{rcl} E&=&\dfrac{3\sqrt{2}-1}{\sqrt{2}}\\\\&=&\dfrac{(3\sqrt{2}-1)\times\sqrt{2}}{(\sqrt{2})\times(\sqrt{2})}\\\\&=&\dfrac{3\sqrt{2}\times\sqrt{2}-\sqrt{2}}{2}\\\\&=&\dfrac{3\times 2-\sqrt{2}}{2}\\\\&=&\dfrac{6-\sqrt{2}}{2}\end{array}$
Donc, $\boxed{E=\dfrac{6-\sqrt{2}}{2}}$
Encadrons $E$ à $10^{-2}$ près sachant que $1.414<\sqrt{2}<1.415.$
On a : $1.414<\sqrt{2}<1.415$
Alors, on multiplie chaque membre de l'inégalité par $-1$ en changeant le sens des inégalités.
On obtient :
$$-1.414>-\sqrt{2}>-1.415$$
En ajoutant $6$ à chaque membre, on obtient :
$$6-1.414>6-\sqrt{2}>6-1.415$$
C'est-à-dire ; $4.586>6-\sqrt{2}>4.585$
On divise chaque membre de l'inégalité par le même nombre $2.$
On trouve alors :
$$\dfrac{4.586}{2}>\dfrac{6-\sqrt{2}}{2}>\dfrac{4.585}{2}$$
Ce qui donne : $2.293>\dfrac{6-\sqrt{2}}{2}>2.292$
Ce qui s'écrit encore : $2.292<\dfrac{6-\sqrt{2}}{2}<2.293$
D'où, un encadrement de $E$ à $10^{-2}$ prés est donné par :
$$\boxed{2.29<\dfrac{6-\sqrt{2}}{2}<2.30}$$
3) Soit $F=\sqrt{2}\sqrt{48}-3\sqrt{54}+5\sqrt{6}.$
Montrons que $F=0$
$\begin{array}{rcl} F&=&\sqrt{2}\sqrt{48}-3\sqrt{54}+5\sqrt{6}\\\\&=&\sqrt{2}\times\sqrt{16\times 3}-3\sqrt{9\times 6}+5\sqrt{6}\\\\&=&\sqrt{2}\times\sqrt{16}\times\sqrt{3}-3\sqrt{9}\times\sqrt{6}+5\sqrt{6}\\\\&=&\sqrt{2}\times 4\times\sqrt{3}-3\times 3\times\sqrt{6}+5\sqrt{6}\\\\&=&4\times\sqrt{2}\times\sqrt{3}-9\sqrt{6}+5\sqrt{6}\\\\&=&4\sqrt{2\times 3}-9\sqrt{6}+5\sqrt{6}\\\\&=&4\sqrt{6}-9\sqrt{6}+5\sqrt{6}\\\\&=&9\sqrt{6}-9\sqrt{6}\\\\&=&0\end{array}$
D'où, $\boxed{F=0}$
Exercice 18
1) On pose $a=1+\sqrt{5}\ $ et $\ b=1-\sqrt{3}$ ; calculons $a^{2}\ $ et $\ b^{2}.$
On a :
$\begin{array}{rcl} a^{2}&=&(1+\sqrt{5})^{2}\\\\&=&(1)^{2}+2\times 1\times\sqrt{5}+(\sqrt{5})^{2}\\\\&=&1+2\sqrt{5}+5\\\\&=&6+2\sqrt{5}\end{array}$
Donc, $\boxed{a^{2}=6+2\sqrt{5}}$
On a :
$\begin{array}{rcl} b^{2}&=&(1-\sqrt{3})^{2}\\\\&=&(1)^{2}-2\times 1\times\sqrt{3}+(\sqrt{3})^{2}\\\\&=&1-2\sqrt{3}+3\\\\&=&4-2\sqrt{3}\end{array}$
Alors, $\boxed{b^{2}=4-2\sqrt{3}}$
2) Simplifions $c=\dfrac{1+\sqrt{5}}{6+2\sqrt{5}}$ puis rendons rationnel son dénominateur.
On remarque que le numérateur de $c$ est égal à $a$ et son dénominateur est égal à $a^{2}.$
Alors, on a :
$\begin{array}{rcl} c&=&\dfrac{1+\sqrt{5}}{6+2\sqrt{5}}\\\\&=&\dfrac{a}{a^{2}}\\\\&=&\dfrac{1}{a}\\\\&=&\dfrac{1}{1+\sqrt{5}}\end{array}$
D'où, $\boxed{c=\dfrac{1}{1+\sqrt{5}}}$
Rendons rationnel le dénominateur.
On a :
$\begin{array}{rcl} c&=&\dfrac{1}{1+\sqrt{5}}\\\\&=&\dfrac{1\times(1-\sqrt{5})}{(1+\sqrt{5})(1-\sqrt{5})}\\\\&=&\dfrac{1-\sqrt{5}}{(1)^{2}-(\sqrt{5})^{2}}\\\\&=&\dfrac{1-\sqrt{5}}{1-5}\\\\&=&\dfrac{1-\sqrt{5}}{-4}\\\\&=&-\dfrac{1-\sqrt{5}}{4}\end{array}$
3) Calculons $a\times c.$
En multipliant $a$ par $c$, on obtient :
$\begin{array}{rcl} a\times c&=&(1+\sqrt{5})\times\dfrac{1}{1+\sqrt{5}}\\\\&=&\dfrac{1+\sqrt{5}}{1+\sqrt{5}}\\\\&=&1\end{array}$
Ainsi, $\boxed{a\times c=1}$
Comme $a\times c=1$ alors, $a$ est l'inverse de $c.$
4) On donne : $A=\sqrt{(6-2\sqrt{5})^{2}-2(6-2\sqrt{5})(3+3\sqrt{5})+(3+3\sqrt{5})^{2}}$
a) Simplifions $A.$
On constate que $(6-2\sqrt{5})^{2}-2(6-2\sqrt{5})(3+3\sqrt{5})+(3+3\sqrt{5})^{2}$ est de la forme $a^{2}-2a.b+b^{2}$ avec $a=(6-2\sqrt{5})\ $ et $\ b=(3+3\sqrt{5}).$
Or, d'après une propriété des identités remarquables, on a :
$$a^{2}-2a.b+b^{2}=(a-b)^{2}$$
Donc,
$\begin{array}{rcl} (6-2\sqrt{5})^{2}-2(6-2\sqrt{5})(3+3\sqrt{5})+(3+3\sqrt{5})^{2}&=&((6-2\sqrt{5})-(3+3\sqrt{5}))^{2}\\\\&=&(6-2\sqrt{5}-3-3\sqrt{5})^{2}\\\\&=&(3-5\sqrt{5})^{2}\end{array}$
Par suite,
$\begin{array}{rcl} A&=&\sqrt{(6-2\sqrt{5})^{2}-2(6-2\sqrt{5})(3+3\sqrt{5})+(3+3\sqrt{5})^{2}}\\\\&=&\sqrt{(3-5\sqrt{5})^{2}}\\\\&=&\left|3-5\sqrt{5}\right|\end{array}$
Cherchons alors le signe de $(3-5\sqrt{5})$
Pour cela, comparons $3\ $ et $\ 5\sqrt{5}$
On a : $3>0\ $ et $\ 5\sqrt{5}>0$
Alors, $3^{2}=9\ $ et $\ (5\sqrt{5})^{2}=125$
Comme $125$ est plus grand que $9$ alors, $3<5\sqrt{5}$
D'où, $3-5\sqrt{5}<0$
Ce qui entraine : $\left|3-5\sqrt{5}\right|=-(3-5\sqrt{5})=-3+5\sqrt{5}$
Par conséquent, $\boxed{A=-3+5\sqrt{5}}$
b) Donnons la valeur approchée de $A$ à $10^{-2}$ près par défaut sachant que $2.236<\sqrt{5}< 2.237.$
Alors, multiplions chaque membre de l'inégalité par $5.$
On obtient alors :
$$5\times 2.236<5\sqrt{5}<5\times 2.237$$
Ce qui donne : $11.180<5\sqrt{5}<11.185$
Ajoutons $-3$ à chaque membre.
On trouve alors :
$$-3+11.180<-3+5\sqrt{5}<-3+11.185$$
Ainsi, on obtient :
$$8.180<-3+5\sqrt{5}<8.185$$
D'où, une valeur approchée de $A$ à $10^{-2}$ près par défaut est : $8.18$
Exercice 19
On donne : $a=1-\sqrt{3}\ $ et $\ b=6\sqrt{1-\dfrac{\sqrt{3}}{2}}.$
1) Calculons $a^{2}\ $ et $\ b^{2}.$
On a :
$\begin{array}{rcl} a^{2}&=&(1-\sqrt{3})^{2}\\\\&=&(1)^{2}-2\times 1\times\sqrt{3}+(\sqrt{3})^{2}\\\\&=&1-2\sqrt{3}+3\\\\&=&4-2\sqrt{3}\end{array}$
Donc, $\boxed{a^{2}=4-2\sqrt{3}}$
On a :
$\begin{array}{rcl} b^{2}&=&\left(6\sqrt{1-\dfrac{\sqrt{3}}{2}}\right)^{2}\\\\&=&(6)^{2}\times\left(\sqrt{1-\dfrac{\sqrt{3}}{2}}\right)^{2}\\\\&=&36\times\left(1-\dfrac{\sqrt{3}}{2}\right)\\\\&=&36\times 1-\dfrac{36\times\sqrt{3}}{2}\\\\&=&36-18\sqrt{3}\end{array}$
Alors, $\boxed{b^{2}=36-18\sqrt{3}}$
Montrons que $b=-3a.$
En observant l'expression de $b^{2}$, on peut encore écrire :
$\begin{array}{rcl} b^{2}&=&36-18\sqrt{3}\\\\&=&9(4-2\sqrt{3})\\\\&=&9a^{2}\end{array}$
Ainsi, $\boxed{b^{2}=9a^{2}}$
Par suite, $\sqrt{b^{2}}=\sqrt{9\times a^{2}}=\sqrt{9}\times\sqrt{a^{2}}$
Ce qui donne : $|b|=3\times |a|$
On sait que $b$ est positif donc, $|b|=b$
On obtient alors : $\boxed{b=3\times |a|}$
Cherchons le signe de $a.$
Pour cela, comparons $1\ $ et $\ \sqrt{3}$
On a : $1>0\ $ et $\ \sqrt{3}>0$
Alors, $1^{2}=1\ $ et $\ (\sqrt{3})^{2}=3$
Comme $1$ est plus petit que $3$ alors, $1<\sqrt{3}$
Donc, $1-\sqrt{3}<0$
Ce qui signifie que $a$ est négatif.
D'où, $|a|=-a.$
Par conséquent,
$\begin{array}{rcl} b&=&3\times|a|\\\\&=&3\times(-a)\\\\&=&-3a\end{array}$
Ce montre que $\boxed{b=-3a}$
2) On donne : $E=\dfrac{2-\sqrt{12}}{6\sqrt{1-\dfrac{\sqrt{3}}{2}}}$ ; montrons que $E$ est un rationnel.
Pour cela, on va montrer que $E$ peut encore s'écrire sans le signe radical.
En observant l'expression de $E$, on constate que son dénominateur est égal à $b.$
Or, on vient de montrer que $b=-3a$ donc, en remplaçant successivement le dénominateur par $b$ et par $-3a$, on obtient :
$\begin{array}{rcl} E&=&\dfrac{2-\sqrt{12}}{6\sqrt{1-\dfrac{\sqrt{3}}{2}}}\\\\&=&\dfrac{2-\sqrt{4\times 3}}{b}\\\\&=&\dfrac{2-\sqrt{4}\times\sqrt{3}}{-3a}\\\\&=&\dfrac{2-2\sqrt{3}}{-3(1-\sqrt{3})}\\\\&=&\dfrac{2(1-\sqrt{3})}{-3(1-\sqrt{3})}\\\\&=&\dfrac{2}{-3}\end{array}$
D'où, $\boxed{E=\dfrac{2}{-3}\quad\text{qui est bien un nombre rationnel}}$
Exercice 20 "BFEM 2008"
On donne : $a=\sqrt{7+4\sqrt{3}}\ $ et $\ b=\sqrt{7-4\sqrt{3}}$
1) Calculons $a^{2}\;;\ b^{2}\;;\ a\times b\;;\ (a+b)^{2}\ $ et $\ (a-b)^{2}$
On a :
$\begin{array}{rcl} a^{2}&=&\left(\sqrt{7+4\sqrt{3}}\right)^{2}\\\\&=&7+4\sqrt{3}\end{array}$
Donc, $\boxed{a^{2}=7+4\sqrt{3}}$
On a :
$\begin{array}{rcl} b^{2}&=&\left(\sqrt{7-4\sqrt{3}}\right)^{2}\\\\&=&7-4\sqrt{3}\end{array}$
Alors, $\boxed{b^{2}=7-4\sqrt{3}}$
On a :
$\begin{array}{rcl} a\times b&=&\sqrt{7+4\sqrt{3}}\times\sqrt{7-4\sqrt{3}}\\\\&=&\sqrt{(7+4\sqrt{3})\times(7-4\sqrt{3})}\\\\&=&\sqrt{(7)^{2}-(4\sqrt{3})^{2}}\\\\&=&\sqrt{49-16\times 3}\\\\&=&\sqrt{49-48}\\\\&=&\sqrt{1}\\\\&=&1\end{array}$
Ainsi, $\boxed{a\times b=1}$
On a :
$\begin{array}{rcl} (a+b)^{2}&=&a^{2}+2\times a\times b+b^{2}\\\\&=&7+4\sqrt{3}+2\times 1+7-4\sqrt{3}\\\\&=&7+2+7\\\\&=&16\end{array}$
Donc, $\boxed{(a+b)^{2}=16}$
On a :
$\begin{array}{rcl} (a-b)^{2}&=&a^{2}-2\times a\times b+b^{2}\\\\&=&7+4\sqrt{3}-2\times 1+7-4\sqrt{3}\\\\&=&7-2+7\\\\&=&12\end{array}$
D'où, $\boxed{(a-b)^{2}=12}$
2) En déduisons $a+b\ $ et $\ a-b$
D'après le résultat de la question $1)$, on a : $(a+b)^{2}=16.$
Ce qui entraine : $\sqrt{(a+b)^{2}}=\sqrt{16}=4$
Or, on sait que : $\sqrt{(a+b)^{2}}=|a+b|$
Donc, on a : $|a+b|=4$
Ce qui signifie que : $a+b=4$ ou bien $a+b=-4$
Mais comme $a\ $ et $\ b$ sont tous les deux positifs alors, leur somme $a+b$ est aussi positif.
Donc, $a+b$ prend la valeur $4$ qui est positive.
D'où, $\boxed{a+b=4}$
Aussi, d'après le résultat de la question $1)$, on a : $(a-b)^{2}=12.$
Ce qui entraine : $\sqrt{(a-b)^{2}}=\sqrt{12}$
Comme $\sqrt{(a-b)^{2}}=|a-b|$ alors, on a : $|a-b|=\sqrt{12}$
Ce qui signifie que : $a-b=\sqrt{12}$ ou bien $a-b=-\sqrt{12}$
Cherchons alors le signe de $a-b$ en comparant $a\ $ et $\ b.$
On a : $a>0\ $ et $\ b>0$
Alors, $a^{2}=7+4\sqrt{3}\ $ et $\ b^{2}=7-4\sqrt{3}$
On remarque que $a^{2}$ est plus grand que $b^{2}.$
Donc, $a$ est supérieur à $b.$
Ce qui signifie que : $a-b$ est positif.
Par conséquent, $a-b$ prend la valeur $\sqrt{12}$ qui est positive.
D'où, $\boxed{a-b=\sqrt{12}=2\sqrt{3}}$
Exercice 21
Soit $A=\sqrt{2}-3\ $ et $\ B=\dfrac{5\sqrt{2}-1}{\sqrt{2}+1}$
1) Calculons $A^{2}$ puis rendons rationnel le dénominateur de $B.$
On a :
$\begin{array}{rcl} A^{2}&=&(\sqrt{2}-3)^{2}\\\\&=&(\sqrt{2})^{2}-2\times 3\times\sqrt{2}+(3)^{2}\\\\&=&2-6\sqrt{2}+9\\\\&=&11-6\sqrt{2}\end{array}$
Donc, $\boxed{A^{2}=11-6\sqrt{2}}$
Pour rendre rationnel le dénominateur de $B$, on multiplie son numérateur et son dénominateur par le même nombre $\sqrt{2}-1.$
Alors, on a :
$\begin{array}{rcl} B&=&\dfrac{5\sqrt{2}-1}{\sqrt{2}+1}\\\\&=&\dfrac{(5\sqrt{2}-1)(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)}\\\\&=&\dfrac{5\sqrt{2}\times\sqrt{2}-5\sqrt{2}-\sqrt{2}+1}{(\sqrt{2})^{2}-(1)^{2}}\\\\&=&\dfrac{5\times 2-6\sqrt{2}+1}{2-1}\\\\&=&\dfrac{10-6\sqrt{2}+1}{1}\\\\&=&11-6\sqrt{2}+1\end{array}$
Ainsi, $\boxed{B=11-6\sqrt{2}}$
2) En déduisons une écriture simplifiée de $\sqrt{B}.$
D'après le résultat de la question $1)$, on constate $B$ est égal à $A^{2}.$
Donc, $\sqrt{B}=\sqrt{A^{2}}=|A|$
Cherchons le signe de $A$ en comparant $\sqrt{2}\ $ et $\ 3.$
Comme $\sqrt{2}\ $ et $\ 3$ sont tous les deux positifs alors, comparons leur carré.
On a : $(\sqrt{2})^{2}=2\ $ et $\ 3^{2}=9$
Or, $2$ est plus petit que $9$ donc, $\sqrt{2}<3$
Ce qui entraine : $\sqrt{2}-6<0.$
Ce qui signifie que : $A$ est négatif.
Ainsi, $|A|=-A$
Donc,
$\begin{array}{rcl}\sqrt{B}&=&|A|\\\\&=&-A\\\\&=&-(\sqrt{2}-3)\\\\&=&-\sqrt{2}+3\end{array}$
D'où, $\boxed{\sqrt{B}=3-\sqrt{2}}$
Résolvons dans $\mathbb{R}$, l'équation :
$$(\sqrt{2}+1)x^{2}-5\sqrt{2}+1=0$$
On a :
$\begin{array}{rcl}(\sqrt{2}+1)x^{2}-5\sqrt{2}+1=0&\Leftrightarrow&(\sqrt{2}+1)x^{2}=-(-5\sqrt{2}+1)\\\\&\Leftrightarrow&(\sqrt{2}+1)x^{2}=5\sqrt{2}-1\\\\&\Leftrightarrow&x^{2}=\dfrac{5\sqrt{2}-1}{\sqrt{2}+1}\\\\&\Leftrightarrow&x^{2}=B\\\\&\Leftrightarrow&\sqrt{x^{2}}=\sqrt{B}\\\\&\Leftrightarrow&|x|=\sqrt{B}\\\\&\Leftrightarrow&x=\sqrt{B}\ \text{ ou bien }\ x=-\sqrt{B}\\\\&\Leftrightarrow&x=3-\sqrt{2}\ \text{ ou bien }\ x=-(3-\sqrt{2})\\\\&\Leftrightarrow&x=3-\sqrt{2}\ \text{ ou bien }\ x=-3+\sqrt{2}\end{array}$
D'où, $\boxed{S=\left\lbrace 3-\sqrt{2}\;;\ -3+\sqrt{2}\right\rbrace}$
Exercice 22
1) Comparons en justifiant :
$$\dfrac{-2\sqrt{3}}{3}\ \text{ et }\ \dfrac{\sqrt{2}}{7}$$
On remarque que $\dfrac{-2\sqrt{3}}{3}<0\ $ et $\ \dfrac{\sqrt{2}}{7}>0.$
Or, on sait que tout nombre positif est supérieur à tout nombre négatif.
Donc, $\boxed{\dfrac{\sqrt{2}}{7}>\dfrac{-2\sqrt{3}}{3}}$
$$\sqrt{7}+4\ \text{ et }\ \sqrt{7}-1$$
En faisant la différence entre ces deux nombres, on trouve :
$\begin{array}{rcl} (\sqrt{7}+4)-(\sqrt{7}-1)&=&\sqrt{7}+4-\sqrt{7}+1\\\\&=&5\end{array}$
On constate que cette différence est un nombre positif.
Ce qui signifie que : $\boxed{\sqrt{7}+4>\sqrt{7}-1}$
$$2\sqrt{2}-1\ \text{ et }\ 3-\sqrt{2}$$
En faisant la différence entre ces deux nombres, on obtient :
$\begin{array}{rcl} (2\sqrt{2}-1)-(3-\sqrt{2})&=&2\sqrt{2}-1-3+\sqrt{2}\\\\&=&3\sqrt{2}-4\end{array}$
Donc, cette différence est égale à $3\sqrt{2}-4.$
Cherchons alors le signe de $3\sqrt{2}-4.$
On a : $4>0\ $ et $\ 3\sqrt{2}>0$
Alors, $(4)^{2}=16\ $ et $\ (3\sqrt{2})^{2}=18$
Comme $18$ est plus grand que $16$ alors, $3\sqrt{2}>4.$
D'où, $3\sqrt{2}-4>0$
Ce qui signifie que la différence $(2\sqrt{2}-1)-(3-\sqrt{2})$ est positive.
Par conséquent, $\boxed{2\sqrt{2}-1>3-\sqrt{2}}$
$$\sqrt{9+4\sqrt{5}}\ \text{ et }\ \sqrt{9-4\sqrt{5}}$$
Comme ces deux nombres sont positifs alors, comparons leur carré.
On a : $\left((\sqrt{9+4\sqrt{5}}\right)^{2}=9+4\sqrt{5}\ $ et $\ \left(\sqrt{9-4\sqrt{5}}\right)^{2}=9-4\sqrt{5}$
Alors, en faisant la différence entre les carrés de ces deux nombres, on obtient :
$\begin{array}{rcl} \left((\sqrt{9+4\sqrt{5}}\right)^{2}-\left(\sqrt{9-4\sqrt{5}}\right)^{2}&=&(9+4\sqrt{5})-(9-4\sqrt{5})\\\\&=&9+4\sqrt{5}-9+4\sqrt{5}\\\\&=&8\sqrt{5}\end{array}$
Donc, cette différence est égale à $8\sqrt{5}$ qui est un nombre positif.
Ce qui signifie que : $\left((\sqrt{9+4\sqrt{5}}\right)^{2}$ est plus grand que $\left(\sqrt{9-4\sqrt{5}}\right)^{2}$
D'où, $\boxed{\sqrt{9+4\sqrt{5}}>\sqrt{9-4\sqrt{5}}}$
2) Écrivons plus simplement :
Soit le nombre $\sqrt{2^{2}\times 4^{2}\times 3^{2}\times 5^{2}}$
Alors, on a :
$\begin{array}{rcl}\sqrt{2^{2}\times 4^{2}\times 3^{2}\times 5^{2}}&=&\sqrt{(2\times 4\times 3\times 5)^{2}}\\\\&=&2\times 4\times 3\times 5\\\\&=&120\end{array}$
D'où, $\boxed{\sqrt{2^{2}\times 4^{2}\times 3^{2}\times 5^{2}}=120}$
Soit le nombre $\sqrt{7^{2}\times 2^{2}\times 5^{3}\times 3^{8}}$
Alors, on a :
$\begin{array}{rcl}\sqrt{7^{2}\times 2^{2}\times 5^{3}\times 3^{8}}&=&\sqrt{7^{2}\times 2^{2}\times 5^{2}\times 5\times(3^{4})^{2}}\\\\&=&\sqrt{(7\times 2\times 5\times 3^{4})^{2}\times 5}\\\\&=&\sqrt{(7\times 2\times 5\times 3^{4})^{2}}\times\sqrt{5}\\\\&=&7\times 2\times 5\times 3^{4}\sqrt{5}\\\\&=&5\,670\sqrt{5}\end{array}$
Ainsi, $\boxed{\sqrt{7^{2}\times 2^{2}\times 5^{3}\times 3^{8}}=5\,670\sqrt{5}}$
Soit le nombre $\sqrt{36^{2}\times b^{5}\times c^{4}\times a^{-2}}$ avec $a>0\ $ et $\ b\geq 0$
Alors, on a :
$\begin{array}{rcl}\sqrt{36^{2}\times b^{5}\times c^{4}\times a^{-2}}&=&\sqrt{36^{2}\times b^{4}\times b\times(c^{2})^{2}\times\dfrac{1}{ a^{2}}}\\\\&=&\sqrt{\dfrac{36^{2}\times(b^{2})^{2}\times b\times(c^{2})^{2}}{a^{2}}}\\\\&=&\dfrac{\sqrt{(36\times b^{2}\times c^{2})^{2}\times b}}{\sqrt{a^{2}}}\\\\&=&\dfrac{\sqrt{(36\times b^{2}\times c^{2})^{2}}\times\sqrt{b}}{|a|}\quad\text{or, }|a|=a\ \text{car }a>0\\\\&=&\dfrac{36\times b^{2}\times c^{2}\times\sqrt{b}}{a}\\\\&=&\dfrac{(6bc)^{2}\sqrt{b}}{a}\end{array}$
D'où, $\boxed{\sqrt{36^{2}\times b^{5}\times c^{4}\times a^{-2}}=\dfrac{(6bc)^{2}\sqrt{b}}{a}}$
Soit le nombre $\sqrt{4+\sqrt{29-\sqrt{14+\sqrt{3+\sqrt{1}}}}}$
Alors, en calculant de la droite vers la gauche, on obtient :
$\begin{array}{rcl}\sqrt{4+\sqrt{29-\sqrt{14+\sqrt{3+\sqrt{1}}}}}&=&\sqrt{4+\sqrt{29-\sqrt{14+\sqrt{3+1}}}}\\\\&=&\sqrt{4+\sqrt{29-\sqrt{14+\sqrt{4}}}}\\\\&=&\sqrt{4+\sqrt{29-\sqrt{14+2}}}\\\\&=&\sqrt{4+\sqrt{29-\sqrt{16}}}\\\\&=&\sqrt{4+\sqrt{29-4}}\\\\&=&\sqrt{4+\sqrt{25}}\\\\&=&\sqrt{4+5}\\\\&=&\sqrt{9}\\\\&=&3\end{array}$
Ainsi, $\boxed{\sqrt{4+\sqrt{29-\sqrt{14+\sqrt{3+\sqrt{1}}}}}=3}$
Soit le nombre $\dfrac{1}{4}\sqrt{13+\sqrt{\dfrac{15}{2}+3\sqrt{\dfrac{1}{4}}}}$
En calculant de la droite vers la gauche, on obtient :
$\begin{array}{rcl}\dfrac{1}{4}\sqrt{13+\sqrt{\dfrac{15}{2}+3\sqrt{\dfrac{1}{4}}}}&=&\dfrac{1}{4}\sqrt{13+\sqrt{\dfrac{15}{2}+3\times\dfrac{\sqrt{1}}{\sqrt{4}}}}\\\\&=&\dfrac{1}{4}\sqrt{13+\sqrt{\dfrac{15}{2}+3\times\dfrac{1}{2}}}\\\\&=&\dfrac{1}{4}\sqrt{13+\sqrt{\dfrac{15}{2}+\dfrac{3}{2}}}\\\\&=&\dfrac{1}{4}\sqrt{13+\sqrt{\dfrac{18}{2}}}\\\\&=&\dfrac{1}{4}\sqrt{13+\sqrt{9}}\\\\&=&\dfrac{1}{4}\sqrt{13+3}\\\\&=&\dfrac{1}{4}\sqrt{16}\\\\&=&\dfrac{1}{4}\times 4\\\\&=&\dfrac{4}{4}\\\\&=&1\end{array}$
D'où, $\boxed{\dfrac{1}{4}\sqrt{13+\sqrt{\dfrac{15}{2}+3\sqrt{\dfrac{1}{4}}}}=1}$
Exercice 23
On donne : $P=2-\dfrac{3\sqrt{2}}{2}\ $ et $\ Q=\dfrac{1}{3\sqrt{2}+4}$
1) Montrons que $P\ $ et $\ Q$ sont des opposés.
Pour cela, on vérifie que la somme $P+Q$ est égale à zéro $(0).$ Ce qui signifie que $P=-Q.$
D'abord, rendons rationnel le dénominateur de $Q.$
On a alors :
$\begin{array}{rcl} Q&=&\dfrac{1}{3\sqrt{2}+4}\\\\&=&\dfrac{3\sqrt{2}-4}{(3\sqrt{2}+4)(3\sqrt{2}-4)}\\\\&=&\dfrac{3\sqrt{2}-4}{(3\sqrt{2})^{2}-(4)^{2}}\\\\&=&\dfrac{3\sqrt{2}-4}{(9\times 2)-(16)}\\\\&=&\dfrac{3\sqrt{2}-4}{18-16}\\\\&=&\dfrac{3\sqrt{2}-4}{2}\\\\&=&\dfrac{3\sqrt{2}}{2}-\dfrac{4}{2}\\\\&=&\dfrac{3\sqrt{2}}{2}-2\end{array}$
Donc, $\boxed{Q=-2+\dfrac{3\sqrt{2}}{2}}$
Ensuite, calculons la somme $P+Q.$
On obtient :
$\begin{array}{rcl} P+Q&=&2-\dfrac{3\sqrt{2}}{2}-2+\dfrac{3\sqrt{2}}{2}\\\\&=&2-2-\dfrac{3\sqrt{2}}{2}+\dfrac{3\sqrt{2}}{2}\\\\&=&0\end{array}$
Ainsi, $\boxed{P+Q=0}$
On constate alors que la somme $P+Q$ est égale à $0.$ Ce qui montre que $P\ $ et $\ Q$ sont des opposés.
2) Sachant que $1.414<\sqrt{2}<1.415$. Encadrons à $10^{-2}$ près $P\ $ et $\ Q$
$-\ $ Encadrement de $Q$
On sait que : $1.414<\sqrt{2}<1.415$
Alors, on multiplie chaque membre de l'inégalité par $3.$
On obtient :
$$3\times 1.414<3\sqrt{2}<3\times 1.415$$
Ce qui donne : $4.242<3\sqrt{2}<4.245$
On divise ensuite chaque membre de l'inégalité par le même nombre $2.$
On trouve alors :
$$\dfrac{4.242}{2}<\dfrac{3\sqrt{2}}{2}<\dfrac{4.245}{2}$$
Ce qui est égal à : $2.121<\dfrac{3\sqrt{2}}{2}<2.122$
En ajoutant le nombre $-2$ à chaque membre de cette dernière inégalité, on obtient :
$$-2+2.121<-2+\dfrac{3\sqrt{2}}{2}<-2+2.122$$
C'est-à-dire ; $0.121<-2+\dfrac{3\sqrt{2}}{2}<0.122$
D'où, un encadrement de $Q$ à $10^{-2}$ prés est donné par :
$$\boxed{0.12<Q<0.13}$$
$-\ $ Encadrement de $P$
Comme $P\ $ et $\ Q$ sont des opposés alors, on a : $P=-Q.$
Donc, pour obtenir un encadrement de $P$, il suffit de multiplier chaque membre de l'encadrement de $Q$ par $-1$ en changeant le sens des inégalités.
On obtient alors :
$$-1\times 0.12>-1\times\left(-2+\dfrac{3\sqrt{2}}{2}\right)>-1\times 0.13$$
Ce qui donne : $-0.12>2-\dfrac{3\sqrt{2}}{2}>-0.13$
Ce qui peut encore s'écrire : $-0.13<2-\dfrac{3\sqrt{2}}{2}<-0.12$
D'où, un encadrement de $P$ à $10^{-2}$ prés est donné par :
$$\boxed{-0.13<P<-0.12}$$
3) On donne : $3.316<\sqrt{11}<3.317$ encadrons à $10^{-1}$ près $\dfrac{a}{b}$ sachant que $a=2\sqrt{11}-6\ $ et $\ b=2\sqrt{11}+6$
Déterminons d'abord l'expression de $\dfrac{a}{b}$
On a :
$\begin{array}{rcl}\dfrac{a}{b}&=&\dfrac{2\sqrt{11}-6}{2\sqrt{11}+6}\\\\&=&\dfrac{2(\sqrt{11}-3)}{2(\sqrt{11}+3)}\\\\&=&\dfrac{\sqrt{11}-3}{\sqrt{11}+3}\\\\&=&\dfrac{(\sqrt{11}-3)(\sqrt{11}-3)}{(\sqrt{11}+3)(\sqrt{11}-3)}\\\\&=&\dfrac{(\sqrt{11}-3)^{2}}{(\sqrt{11})^{2}-(3)^{2}}\\\\&=&\dfrac{(\sqrt{11})^{2}-2\times 3\times\sqrt{11}+(3)^{2}}{11-9}\\\\&=&\dfrac{11-6\sqrt{11}+9}{2}\\\\&=&\dfrac{20-6\sqrt{11}}{2}\\\\&=&\dfrac{2(10-3\sqrt{11})}{2}\\\\&=&10-3\sqrt{11}\end{array}$
Ainsi, $\boxed{\dfrac{a}{b}=10-3\sqrt{11}}$
Donnons ensuite un encadrement de $(10-3\sqrt{11})$ à $10^{-1}$ près
On sait que : $3.316<\sqrt{11}<3.317$
Alors, on multiplie chaque membre de l'inégalité par $-3$ en changeant le sens des inégalités.
On obtient :
$$-3\times 3.316>-3\sqrt{11}>-3\times 3.317$$
Ce qui donne : $-9.948>-3\sqrt{11}>-9.951$
On divise ensuite chaque membre de l'inégalité par le même nombre $2.$
En ajoutant le nombre $10$ à chaque membre de cette dernière inégalité, on obtient :
$$10-9.948>10-3\sqrt{11}>10-9.951$$
C'est-à-dire ; $0.052>10-3\sqrt{11}>0.049$
Ce qui peut encore s'écrire : $0.049<10-3\sqrt{11}<0.052$
D'où, un encadrement de $\dfrac{a}{b}$ à $10^{-1}$ prés est donné par :
$$\boxed{0<\dfrac{a}{b}<0.1}$$
Exercice 24
On donne : $a=\sqrt{28+16\sqrt{3}}\ $ et $\ b=\sqrt{28-16\sqrt{3}}$
1) Montrons que $a\times b=4$
Pour cela, calculons le produit $a\times b.$
On a :
$\begin{array}{rcl} a\times b&=&\sqrt{28+16\sqrt{3}}\times\sqrt{28-16\sqrt{3}}\\\\&=&\sqrt{(28+16\sqrt{3})\times(28-16\sqrt{3})}\\\\&=&\sqrt{(28)^{2}-(16\sqrt{3})^{2}}\\\\&=&\sqrt{(784)-(16^{2}\times\sqrt{3}^{2})}\\\\&=&\sqrt{(784)-(256\times 3)}\\\\&=&\sqrt{784-768}\\\\&=&\sqrt{16}\\\\&=&4\end{array}$
D'où, $\boxed{a\times b=4}$
2) On pose $u= a+b\ $ et $\ v=a-b$. Calculons $u^{2}\ $ et $\ v^{2}$ puis en déduisons $u\ $ et $\ v.$
Soit $u=a+b$ alors, $u^{2}=(a+b)^{2}.$
Donc, d'après la propriété des identités remarquables, on a :
$\begin{array}{rcl} u^{2}&=&(a+b)^{2}\\\\&=&a^{2}+2\times a\times b+b^{2}\\\\&=&\left(\sqrt{28+16\sqrt{3}}\right)^{2}+2\times 4+\left(\sqrt{28-16\sqrt{3}}\right)^{2}\\\\&=&28+16\sqrt{3}+8+28-16\sqrt{3}\\\\&=&64\end{array}$
D'où, $\boxed{u^{2}=64}$
Soit $v=a-b$ alors, $v^{2}=(a-b)^{2}.$
Donc, d'après la propriété des identités remarquables, on obtient :
$\begin{array}{rcl} v^{2}&=&(a-b)^{2}\\\\&=&a^{2}-2\times a\times b+b^{2}\\\\&=&\left(\sqrt{28+16\sqrt{3}}\right)^{2}-2\times 4+\left(\sqrt{28-16\sqrt{3}}\right)^{2}\\\\&=&28+16\sqrt{3}-8+28-16\sqrt{3}\\\\&=&48\end{array}$
Ainsi, $\boxed{v^{2}=48}$
En déduisons $u\ $ et $\ v.$
On sait que : $u^{2}=64$
Alors, $\sqrt{u^{2}}=\sqrt{64}=8$
Or, $\sqrt{u^{2}}=|u|$ donc, $|u|=8$
Cherchons alors le signe de $u.$
On a : $u=a+b$, ce qui signifie que $u$ est la somme de deux nombres positifs.
Donc, $u$ est positif.
D'où, $|u|=u$
Par conséquent, $\boxed{u=8}$
Aussi, on sait que : $v^{2}=48$
Donc, $\sqrt{v^{2}}=\sqrt{48}=4\sqrt{3}$
Comme, $\sqrt{v^{2}}=|v|$ alors, on a : $|v|=4\sqrt{3}$
Cherchons le signe de $v.$
On a : $v=a-b$
Donc, comparons $a\ $ et $\ b$
Ces deux nombres étant positifs alors, comparons leur carré.
On a :
$a^{2}=\left(\sqrt{28+16\sqrt{3}}\right)^{2}=28+16\sqrt{3}$
$b^{2}=\left(\sqrt{28-16\sqrt{3}}\right)^{2}=28-16\sqrt{3}$
En faisant la différence entre les carrés de ces deux nombres, on obtient :
$\begin{array}{rcl} a^{2}-b^{2}&=&\left(\sqrt{28+16\sqrt{3}}\right)^{2}-\left(\sqrt{28-16\sqrt{3}}\right)^{2}\\\\&=&28+16\sqrt{3}-(28-16\sqrt{3})\\\\&=&28+16\sqrt{3}-28+16\sqrt{3}\\\\&=&32\sqrt{3}\end{array}$
On remarque alors que cette différence $32\sqrt{3}$ est positive.
Ce qui signifie que $a$ est supérieur à $b$
Ainsi, $v$ est positif
D'où, $|v|=v$
Or, $|v|=4\sqrt{3}$
Par conséquent, $\boxed{v=4\sqrt{3}}$
3) On donne $X=\dfrac{u+v}{2}\ $ et $\ Y=\dfrac{u-v}{2}.$ Trouvons $X\ $ et $\ Y$ puis montrons que $a=X\ $ et $\ b=Y.$
Soit $X=\dfrac{u+v}{2}$ alors, en remplaçant $u\ $ et $\ v$ par leur valeur, on obtient :
$\begin{array}{rcl} X&=&\dfrac{u+v}{2}\\\\&=&\dfrac{8+4\sqrt{3}}{2}\\\\&=&\dfrac{2(4+2\sqrt{3})}{2}\\\\&=&4+2\sqrt{3}\end{array}$
D'où, $\boxed{X=4+2\sqrt{3}}$
On a : $Y=\dfrac{u-v}{2}$ alors, en remplaçant $u\ $ et $\ v$ par leur valeur, on trouve :
$\begin{array}{rcl} Y&=&\dfrac{u-v}{2}\\\\&=&\dfrac{8-4\sqrt{3}}{2}\\\\&=&\dfrac{2(4-2\sqrt{3})}{2}\\\\&=&4-2\sqrt{3}\end{array}$
Donc, $\boxed{Y=4-2\sqrt{3}}$
Montrons que $a=X\ $ et $\ b=Y.$
Dans l'expression de $X$, on remplace $u$ par $a+b\ $ et $\ v$ par $a-b.$
On obtient :
$\begin{array}{rcl} X&=&\dfrac{u+v}{2}\\\\&=&\dfrac{(a+b)+(a-b)}{2}\\\\&=&\dfrac{a+b+a-b}{2}\\\\&=&\dfrac{2a}{2}\\\\&=&a\end{array}$
Donc, $\boxed{X=a}$
Dans l'expression de $Y$, remplaçons $u$ par $a+b\ $ et $\ v$ par $a-b.$
On obtient alors :
$\begin{array}{rcl} Y&=&\dfrac{u-v}{2}\\\\&=&\dfrac{(a+b)-(a-b)}{2}\\\\&=&\dfrac{a+b-a+b}{2}\\\\&=&\dfrac{2b}{2}\\\\&=&a\end{array}$
D'où, $\boxed{Y=b}$
4) Donnons la valeur approchée par défaut de $b$ à $10^{-2}$ près sachant que $1.732<\sqrt{3}<1.733$
D'après le résultat de la question $3)$, on sait que : $b=Y$
Donc, $b=4-2\sqrt{3}$
Soit : $1.732<\sqrt{3}<1.733$
Alors, multiplions chaque membre de l'inégalité par $-2$ en changeant le sens des inégalités.
On obtient alors :
$$-2\times 1.732>-2\sqrt{3}>-2\times 1.733$$
Ce qui donne : $-3.464>-2\sqrt{3}>-3.466$
Ajoutons $4$ à chaque membre.
On trouve alors :
$$4-3.464>4-2\sqrt{3}>4-3.466$$
C'est-à-dire ; $0.536>4-2\sqrt{3}>0.534$
Ce qui peut encore s'écrire : $0.534<4-2\sqrt{3}<0.536$
Ainsi, on obtient :
$$0.53<b<0.54$$
D'où, une valeur approchée de $b$ à $10^{-2}$ près par défaut est : $0.53$
Exercice 25
Soient $a\;,\ b\;,\ c$ trois réels tels que :
$$a(\sqrt{3}+1)=\sqrt{3}-1\;,\quad b=\sqrt{2-\sqrt{3}}\quad\text{et}\quad c=\left(\dfrac{\sqrt{6}-\sqrt{2}}{2}\right)^{2}$$
1) Calculons $a$ et rendons rationnel son dénominateur.
On sait que : $a(\sqrt{3}+1)=\sqrt{3}-1$
Ce qui entraine alors : $\boxed{a=\dfrac{\sqrt{3}-1}{\sqrt{3}+1}}$
Soit alors, $(\sqrt{3}-1)$ l'expression conjuguée du dénominateur.
Donc, pour rendre rationnel le dénominateur de $a$, on multiplie son numérateur et son dénominateur par le même nombre $(\sqrt{3}-1).$
On obtient alors :
$\begin{array}{rcl} a&=&\dfrac{\sqrt{3}-1}{\sqrt{3}+1}\\\\&=&\dfrac{(\sqrt{3}-1)(\sqrt{3}-1)}{(\sqrt{3}+1)(\sqrt{3}-1)}\\\\&=&\dfrac{(\sqrt{3}-1)^{2}}{(\sqrt{3})^{2}-(1)^{2}}\\\\&=&\dfrac{(\sqrt{3}-1)^{2}}{3-1}\\\\&=&\dfrac{(\sqrt{3}-1)^{2}}{2}\end{array}$
D'où, $\boxed{a=\dfrac{(\sqrt{3}-1)^{2}}{2}}$
2) Écrivons $c$ sous la forme $x+y\sqrt{3}.$
On a :
$\begin{array}{rcl} c&=&\left(\dfrac{\sqrt{6}-\sqrt{2}}{2}\right)^{2}\\\\&=&\dfrac{(\sqrt{6}-\sqrt{2})^{2}}{(2)^{2}}\\\\&=&\dfrac{(\sqrt{6})^{2}-2\times\sqrt{2}\times\sqrt{6}+(\sqrt{2})^{2}}{4}\\\\&=&\dfrac{6-2\times\sqrt{2}\times\sqrt{2\times 3}+2}{4}\\\\&=&\dfrac{8-2\times\sqrt{2}\times\sqrt{2}\times\sqrt{3}}{4}\\\\&=&\dfrac{8-2\times 2\times\sqrt{3}}{4}\\\\&=&\dfrac{8-4\sqrt{3}}{4}\\\\&=&\dfrac{4(2-\sqrt{3})}{4}\\\\&=&2-\sqrt{3}\end{array}$
Alors, $\boxed{c=2-\sqrt{3}}$
3) a) Montrons que $a=c$ puis en déduisons une écriture simplifiée de $b.$
Soit $a=\dfrac{(\sqrt{3}-1)^{2}}{2}.$
Alors, en développant cette expression de $a$, on obtient :
$\begin{array}{rcl} a&=&\dfrac{(\sqrt{3}-1)^{2}}{2}\\\\&=&\dfrac{(\sqrt{3})^{2}-2\times 1\times\sqrt{3}+(1)^{2}}{2}\\\\&=&\dfrac{3-2\sqrt{3}+1}{2}\\\\&=&\dfrac{4-2\sqrt{3}}{2}\\\\&=&\dfrac{2(2-\sqrt{3})}{2}\\\\&=&2-\sqrt{3}\end{array}$
D'où, $\boxed{a=2-\sqrt{3}}$
Ce qui montre que $a=c.$
Ainsi, en observant l'expression de $b$, on remarque que : $b=\sqrt{2-\sqrt{3}}=\sqrt{c}.$
Ce qui donne alors :
$\begin{array}{rcl} b&=&\sqrt{c}\\\\&=&\sqrt{\left(\dfrac{\sqrt{6}-\sqrt{2}}{2}\right)^{2}}\\\\&=&\left|\dfrac{\sqrt{6}-\sqrt{2}}{2}\right|\end{array}$
Cherchons alors le signe de $\dfrac{\sqrt{6}-\sqrt{2}}{2}.$
Pour cela, comparons $\sqrt{6}\ $ et $\ \sqrt{2}.$
Ces deux nombres étant positifs alors, comparons leur carré.
On a : $(\sqrt{6})^{2}=6\ $ et $\ (\sqrt{2})^{2}=2$
Comme $6$ est plus grand que $2$ alors, $\sqrt{6}>\sqrt{2}.$
D'où, $\sqrt{6}-\sqrt{2}>0$
Ce qui entraine alors : $\dfrac{\sqrt{6}-\sqrt{2}}{2}>0.$
D'où, $\left|\dfrac{\sqrt{6}-\sqrt{2}}{2}\right|=\dfrac{\sqrt{6}-\sqrt{2}}{2}$
Par conséquent, $\boxed{b=\dfrac{\sqrt{6}-\sqrt{2}}{2}}$
b) Encadrons $b$ à $10^{-1}$ près sachant que $1.414<\sqrt{2}<1.415\ $ et $\ 2.449<\sqrt{6}<2.450$
On a : $1.414<\sqrt{2}<1.415$
Alors, multiplions chaque membre de l'inégalité par $-1$ en changeant le sens des inégalités.
On obtient : $-1.414>-\sqrt{2}>-1.415$
Ce qui peut encore s'écrire :
$$-1.415<-\sqrt{2}<-1.414$$
Aussi, on a :
$$2.449<\sqrt{6}<2.450$$
En additionnant ces deux inégalités ; membre à membre, on obtient :
$$2.449-1.415<\sqrt{6}-\sqrt{2}<2.450-1.414$$
Ce qui donne : $1.034<\sqrt{6}-\sqrt{2}<1.036$
En divisant chaque membre de cette dernière inégalité par $2$, on trouve :
$$\dfrac{1.034}{2}<\dfrac{\sqrt{6}-\sqrt{2}}{2}<\dfrac{1.036}{2}$$
Ce qui est équivalent à : $0.517<\dfrac{\sqrt{6}-\sqrt{2}}{2}<0.518$
D'où, un encadrement de $b$ à $10^{-1}$ près est donné par :
$$\boxed{0.5<b<0.6}$$
Exercice 26
1) Déterminons le réel $a$ tel que $36a=1\,296$ puis en déduisons $\sqrt{1\,296}.$
Pour cela, résolvons l'équation $36a=1\,296.$
On a :
$\begin{array}{rcl} 36a=1\,296&\Leftrightarrow&a=\dfrac{1\,296}{36}\\\\&\Leftrightarrow&a=36\end{array}$
Ainsi, $\boxed{a=36}$
Par suite, $1\,296=36\times 36=36^{2}$
D'où, $\boxed{\sqrt{1\,296}=\sqrt{36^{2}}=36}$
2) On donne : $x=3+2\sqrt{2}\;;\ y=3-2\sqrt{2}\ $ et $\ z=\dfrac{\sqrt{5}+1}{2}$
a) Calculons $x^{2}\;,\ y^{2}\;,\ xy\ $ et $\ \dfrac{x}{y}$
$-\ $ calcul de $x^{2}$
D'après la propriété des identités remarquables, on a :
$\begin{array}{rcl} x^{2}&=&(3+2\sqrt{2})^{2}\\\\&=&(3)^{2}+2\times 3\times 2\sqrt{2}+(2\sqrt{2})^{2}\\\\&=&9+12\sqrt{2}+(4\times 2)\\\\&=&9+12\sqrt{2}+8\\\\&=&17+12\sqrt{2}\end{array}$
Donc, $\boxed{x^{2}=17+12\sqrt{2}}$
$-\ $ calcul de $y^{2}$
D'après la propriété des identités remarquables, on a :
$\begin{array}{rcl} y^{2}&=&(3-2\sqrt{2})^{2}\\\\&=&(3)^{2}-2\times 3\times 2\sqrt{2}+(2\sqrt{2})^{2}\\\\&=&9-12\sqrt{2}+(4\times 2)\\\\&=&9-12\sqrt{2}+8\\\\&=&17-12\sqrt{2}\end{array}$
D'où, $\boxed{y^{2}=17-12\sqrt{2}}$
$-\ $ calcul de $xy$
D'après la propriété des identités remarquables, on a :
$\begin{array}{rcl} xy&=&(3+2\sqrt{2})(3-2\sqrt{2})\\\\&=&(3)^{2}-(2\sqrt{2})^{2}\\\\&=&9-(4\times 2)\\\\&=&9-8\\\\&=&1\end{array}$
Ainsi, $\boxed{xy=1}$
$-\ $ calcul de $\dfrac{x}{y}$
On a :
$\begin{array}{rcl}\dfrac{x}{y}&=&\dfrac{3+2\sqrt{2}}{3-2\sqrt{2}}\\\\&=&\dfrac{(3+2\sqrt{2})(3+2\sqrt{2})}{(3-2\sqrt{2})(3+2\sqrt{2})}\\\\&=&\dfrac{(3+2\sqrt{2})^{2}}{(3)^{2}-(2\sqrt{2})^{2}}\\\\&=&\dfrac{(3)^{2}+2\times 3\times 2\sqrt{2}+(2\sqrt{2})^{2}}{9-(4\times 2)}\\\\&=&\dfrac{9+12\sqrt{2}+8}{9-8}\\\\&=&\dfrac{17+12\sqrt{2}}{1}\\\\&=&17+12\sqrt{2}\end{array}$
D'où, $\boxed{\dfrac{x}{y}=17+12\sqrt{2}}$
b) Montrons que $\dfrac{x}{y}+\dfrac{y}{x}$ est un entier relatif.
En réduisant au même dénominateur, on trouve :
$\begin{array}{rcl} \dfrac{x}{y}+\dfrac{y}{x}&=&\dfrac{x\times x}{x\times y}+\dfrac{y\times y}{x\times y}\\\\&=&\dfrac{x^{2}}{xy}+\dfrac{y^{2}}{xy}\\\\&=&\dfrac{x^{2}+y^{2}}{xy}\end{array}$
Donc, $\boxed{\dfrac{x}{y}+\dfrac{y}{x}=\dfrac{x^{2}+y^{2}}{xy}}$
Puis, en remplaçant $x^{2}\;;\ y^{2}\ $ et $\ xy$ par leur valeur, on obtient :
$\begin{array}{rcl} \dfrac{x}{y}+\dfrac{y}{x}&=&\dfrac{x^{2}+y^{2}}{xy}\\\\&=&\dfrac{17+12\sqrt{2}+17-12\sqrt{2}}{1}\\\\&=&34\end{array}$
D'où, $\boxed{\dfrac{x}{y}+\dfrac{y}{x}=34\quad\text{qui est un entier relatif}}$
Par conséquent, $\dfrac{x}{y}+\dfrac{y}{x}$ est un entier relatif.
c) Montrons que $\dfrac{1}{z}=z-1$
Soit $z=\dfrac{\sqrt{5}+1}{2}$
Alors, $\dfrac{1}{z}=\dfrac{1}{\dfrac{\sqrt{5}+1}{2}}=\dfrac{2}{\sqrt{5}+1}$
Donc, en rendant rationnel le dénominateur, on obtient :
$\begin{array}{rcl}\dfrac{1}{z}&=&\dfrac{2}{\sqrt{5}+1}\\\\&=&\dfrac{2(\sqrt{5}-1)}{(\sqrt{5}+1)(\sqrt{5}-1)}\\\\&=&\dfrac{2(\sqrt{5}-1)}{(\sqrt{5})^{2}-(1)^{2}}\\\\&=&\dfrac{2(\sqrt{5}-1)}{(5-1}\\\\&=&\dfrac{2(\sqrt{5}-1)}{4}\\\\&=&\dfrac{\sqrt{5}-1}{2}\end{array}$
D'où, $\boxed{\dfrac{1}{z}=\dfrac{\sqrt{5}-1}{2}}$
Par ailleurs, en calculant $(z-1)$ on trouve :
$\begin{array}{rcl} z-1&=&\dfrac{\sqrt{5}+1}{2}-1\\\\&=&\dfrac{\sqrt{5}+1-2}{2}\\\\&=&\dfrac{\sqrt{5}-1}{2}\end{array}$
Ainsi, $\boxed{z-1=\dfrac{\sqrt{5}-1}{2}}$
Ce qui montre que $\dfrac{1}{z}=z-1$
Exercice 27
1) On donne : $P=\left(\dfrac{\sqrt{2}-\sqrt{3}}{\sqrt{2}}:\dfrac{1}{\sqrt{2}+\sqrt{3}}\right)\times \dfrac{\sqrt{2}}{4\sqrt{3}}.$
Montrons que $P=\dfrac{\sqrt{3}}{12}.$
En calculant l'expression de $P$, on obtient :
$\begin{array}{rcl} P&=&\dfrac{\dfrac{\sqrt{2}-\sqrt{3}}{\sqrt{2}}}{\dfrac{1}{\sqrt{2}+\sqrt{3}}}\times\dfrac{\sqrt{2}}{4\sqrt{3}}\\\\&=&\dfrac{\sqrt{2}-\sqrt{3}}{\sqrt{2}}\times\dfrac{\sqrt{2}+\sqrt{3}}{1}\times\dfrac{\sqrt{2}}{4\sqrt{3}}\\\\&=&\dfrac{(\sqrt{2}-\sqrt{3})(\sqrt{2}+\sqrt{3})}{4\sqrt{3}}\\\\&=&\dfrac{(\sqrt{2})^{2}-(\sqrt{3})^{2}}{4\sqrt{3}}\\\\&=&\dfrac{2-3}{4\sqrt{3}}\\\\&=&\dfrac{-1}{4\sqrt{3}}\end{array}$
Donc, $P=-\dfrac{1}{4\sqrt{3}}$
En rendant rationnel le dénominateur, on trouve :
$\begin{array}{rcl} P&=&-\dfrac{1}{4\sqrt{3}}\\\\&=&-\dfrac{1\times\sqrt{3}}{4\sqrt{3}\times\sqrt{3}}\\\\&=&-\dfrac{\sqrt{3}}{4\times 3}\\\\&=&-\dfrac{\sqrt{3}}{12}\end{array}$
D'où, $\boxed{P=-\dfrac{\sqrt{3}}{12}}$
2) On donne : $Q=-2\sqrt{48}+3\sqrt{192}-4\sqrt{75}$
a) Écrivons $Q$ sous la forme $a\sqrt{b}\ $ ($a\in\mathbb{Z}\;;\ b\in\mathbb{N}$)
On a :
$\begin{array}{rcl} Q&=&-2\sqrt{48}+3\sqrt{192}-4\sqrt{75}\\\\&=&-2\sqrt{16\times 3}+3\sqrt{64\times 3}-4\sqrt{25\times 3}\\\\&=&-2\sqrt{16}\times\sqrt{3}+3\sqrt{64}\times\sqrt{3}-4\sqrt{25}\times\sqrt{3}\\\\&=&-2\times 4\times\sqrt{3}+3\times 8\times\sqrt{3}-4\times 5\times\sqrt{3}\\\\&=&-8\sqrt{3}+24\sqrt{3}-20\sqrt{3}\\\\&=&-4\sqrt{3}\end{array}$
Ainsi, $\boxed{Q=-4\sqrt{3}}$
b) Encadrons $Q$ par deux entiers consécutifs.
On sait que : $1.732<\sqrt{3}<1.733$
Alors, multiplions chaque membre de l'inégalité par $-4$ en changeant le sens des inégalités.
On obtient :
$$-4\times 1.732>-4\times\sqrt{3}>-4\times 1.733$$
Ce qui donne : $-6.928>-4\sqrt{3}>-6.932$
Ce qui peut encore s'écrire :
$$-6.932<-4\sqrt{3}<-6.928$$
D'où, un encadrement de $Q$ par deux entiers consécutifs est donné par :
$$\boxed{-7<Q<-6}$$
3) Montrons que $P\ $ et $\ Q$ sont des inverses.
Pour cela, il suffit de vérifier que $P\times Q=1.$
En calculant le produit $P\times Q=1$, on trouve :
$\begin{array}{rcl} P\times Q&=&\left(-\dfrac{\sqrt{3}}{12}\right)\times(-4\sqrt{3})\\\\&=&\dfrac{4\sqrt{3}\times\sqrt{3}}{12}\\\\&=&\dfrac{4\times 3}{12}\\\\&=&\dfrac{12}{12}\\\\&=&1\end{array}$
Ainsi, $\boxed{P\times Q=1}$
Ce qui montre que $P\ $ et $\ Q$ sont des inverses.
4) En déduisons que $P(P-1)=\dfrac{P-1}{Q}.$
Comme $P\ $ et $\ Q$ sont des inverses alors, on a : $P\times Q=1$
Ainsi, $Q=\dfrac{1}{P}$
Donc, dans l'expression $\dfrac{P-1}{Q}$, en remplaçant $Q$ par $\dfrac{1}{P}$, on obtient :
$\begin{array}{rcl}\dfrac{P-1}{Q}&=&\dfrac{P-1}{\dfrac{1}{P}}\\\\&=&(P-1)\times\dfrac{P}{1}\\\\&=&(P-1)\times P\end{array}$
D'où, $\boxed{\dfrac{P-1}{Q}=P(P-1)}$
Exercice 28
1) On considère l'expression $X=\sqrt{300}+2\sqrt{3}-4\sqrt{75}.$
Écrivons $X$ sous la forme $a\sqrt{b}$ ; où $a\ $ et $\ b$ sont des entiers relatifs.
On a :
$\begin{array}{rcl} X&=&\sqrt{300}+2\sqrt{3}-4\sqrt{75}\\\\&=&\sqrt{100\times 3}+2\sqrt{3}-4\sqrt{25\times 3}\\\\&=&\sqrt{100}\times\sqrt{3}+2\sqrt{3}-4\sqrt{25}\times\sqrt{3}\\\\&=&10\times\sqrt{3}+2\sqrt{3}-4\times 5\times\sqrt{3}\\\\&=&10\sqrt{3}+2\sqrt{3}-20\sqrt{3}\\\\&=&-8\sqrt{3}\end{array}$
Alors, $\boxed{X=-8\sqrt{3}}$
2) Calculons $\left(2-\sqrt{3}\right)^{2}$ puis déduisons-en l'écriture de $Y=\sqrt{7-4\sqrt{3}}$ avec un seul radical.
On a :
$\begin{array}{rcl} \left(2-\sqrt{3}\right)^{2}&=&(2)^{2}-2\times 2\times \sqrt{3}+(\sqrt{3})^{2}\\\\&=&4-4\sqrt{3}+3\\\\&=&7-4\sqrt{3}\end{array}$
D'où, $\boxed{\left(2-\sqrt{3}\right)^{2}=7-4\sqrt{3}}$
Par suite, dans l'expression de $Y$, en remplaçant $7-4\sqrt{3}$ par $\left(2-\sqrt{3}\right)^{2}$, on obtient :
$\begin{array}{rcl} Y&=&\sqrt{7-4\sqrt{3}}\\\\&=&\sqrt{\left(2-\sqrt{3}\right)^{2}}\\\\&=&\left|2-\sqrt{3}\right|\end{array}$
Cherchons alors le signe de $(2-\sqrt{3}).$
Pour cela, comparons $2\ $ et $\ \sqrt{3}.$
Ces deux nombres étant positifs alors, comparons leur carré.
On a : $(2)^{2}=4\ $ et $\ (\sqrt{3})^{2}=3$
Comme $4$ est plus grand que $3$ alors, $2>\sqrt{3}.$
D'où, $2-\sqrt{3}>0$
Ainsi, $\left|2-\sqrt{3}\right|=2-\sqrt{3}.$
Par conséquent, $\boxed{Y=2-\sqrt{3}}$
Exercice 29
Écrivons le plus simplement possible les expressions suivantes :
$A=5\sqrt{300}+\sqrt{27}-3\sqrt{147}\ $ et $\ B=\dfrac{\sqrt{6-\sqrt{11}}\times\sqrt{6+\sqrt{11}}}{5}.$
On sait que :
$300=100\times 3$
$27=9\times 3$
$147=49\times 3$
Donc, en remplaçant dans l'expression de $A$, on obtient :
$\begin{array}{rcl} A&=&5\sqrt{300}+\sqrt{27}-3\sqrt{147}\\\\&=&5\sqrt{100\times 3}+\sqrt{9\times 3}-3\sqrt{49\times 3}\\\\&=&5\sqrt{100}\times\sqrt{3}+\sqrt{9}\times\sqrt{3}-3\sqrt{49}\times\sqrt{3}\\\\&=&5\times 10\times\sqrt{3}+3\times\sqrt{3}-3\times 7\times\sqrt{3}\\\\&=&50\sqrt{3}+3\sqrt{3}-21\sqrt{3}\\\\&=&32\sqrt{3}\end{array}$
Ainsi, $\boxed{A=32\sqrt{3}}$
En utilisant les propriétés de la racine carrée et des identités remarquables, on obtient :
$\begin{array}{rcl} B&=&\dfrac{\sqrt{6-\sqrt{11}}\times\sqrt{6+\sqrt{11}}}{5}\\\\&=&\dfrac{\sqrt{(6-\sqrt{11})\times(6+\sqrt{11})}}{5}\\\\&=&\dfrac{\sqrt{(6)^{2}-(\sqrt{11})^{2}}}{5}\\\\&=&\dfrac{\sqrt{36-11}}{5}\\\\&=&\dfrac{\sqrt{25}}{5}\\\\&=&\dfrac{5}{5}\\\\&=&1\end{array}$
D'où, $\boxed{B=1}$
Exercice 30
1) Calculons $\left(1+\sqrt{5}\right)^{2}\ $ et $\ \left(1-\sqrt{5}\right)^{2}$
En utilisant une propriété des identités remarquables, on a :
$\begin{array}{rcl} \left(1+\sqrt{5}\right)^{2}&=&(1)^{2}+2\times 1\times \sqrt{5}+(\sqrt{5})^{2}\\\\&=&1+2\sqrt{5}+5\\\\&=&6+2\sqrt{5}\end{array}$
D'où, $\boxed{\left(1+\sqrt{5}\right)^{2}=6+2\sqrt{5}}$
En utilisant une propriété des identités remarquables, on trouve :
$\begin{array}{rcl} \left(1-\sqrt{5}\right)^{2}&=&(1)^{2}-2\times 1\times \sqrt{5}+(\sqrt{5})^{2}\\\\&=&1-2\sqrt{5}+5\\\\&=&6-2\sqrt{5}\end{array}$
Ainsi, $\boxed{\left(1-\sqrt{5}\right)^{2}=6-2\sqrt{5}}$
2) On donne : $X=\sqrt{6-2\sqrt{5}}\ $ et $\ Y=\sqrt{6+2\sqrt{5}}$
a) Écrivons $X\ $ et $\ Y$ avec un seul radical.
Dans l'expression de $X$, en remplaçant $6-2\sqrt{5}$ par $\left(1-\sqrt{5}\right)^{2}$, on trouve :
$\begin{array}{rcl} X&=&\sqrt{6-2\sqrt{5}}\\\\&=&\sqrt{\left(1-\sqrt{5}\right)^{2}}\\\\&=&\left|1-\sqrt{5}\right|\end{array}$
Cherchons alors le signe de $(1-\sqrt{5}).$
Pour cela, comparons $1\ $ et $\ \sqrt{5}.$
Comme ces deux nombres sont positifs alors, comparons leur carré.
On a : $(1)^{2}=1\ $ et $\ (\sqrt{5})^{2}=5$
Comme $1$ est plus petit que $5$ alors, $1<\sqrt{5}.$
D'où, $1-\sqrt{5}<0$
Ainsi, $\left|1-\sqrt{5}\right|=-(1-\sqrt{5})=-1+\sqrt{5}.$
Par conséquent, $\boxed{X=-1+\sqrt{5}}$
Dans l'expression de $Y$, on remplace $6+2\sqrt{5}$ par $\left(1+\sqrt{5}\right)^{2}.$
On obtient alors :
$\begin{array}{rcl} Y&=&\sqrt{6+2\sqrt{5}}\\\\&=&\sqrt{\left(1+\sqrt{5}\right)^{2}}\\\\&=&\left|1+\sqrt{5}\right|\\\\&=&1+\sqrt{5}\end{array}$
D'où, $\boxed{Y=1+\sqrt{5}}$
b) Calculons $X+Y\ $ et $\ X-Y.$
En remplaçant $X\ $ et $\ Y$ par leur expression du résultat de $2)\,a)$, on obtient :
$\begin{array}{rcl} X+Y&=&(-1+\sqrt{5})+(1+\sqrt{5})\\\\&=&-1+\sqrt{5}+1+\sqrt{5}\\\\&=&2\sqrt{5}\end{array}$
Ainsi, $\boxed{X+Y=2\sqrt{5}}$
$\begin{array}{rcl} X-Y&=&(-1+\sqrt{5})-(1+\sqrt{5})\\\\&=&-1+\sqrt{5}-1-\sqrt{5}\\\\&=&-2\end{array}$
Donc, $\boxed{X-Y=-2}$
Exercice 31
On donne : $a=5-2\sqrt{6}\ $ et $\ b=5+2\sqrt{6}.$
1) Calculons $a\times b.$
En utilisant une propriété des identités remarquables, on a :
$\begin{array}{rcl} a\times b&=&(5-2\sqrt{6})(5+2\sqrt{6})\\\\&=&(5)^{2}-(2\sqrt{6})^{2}25-(4\times 6)\\\\&=&25-24\\\\&=&1\end{array}$
Alors, $\boxed{a\times b=1}$
Comme le produit de $a\ $ et $\ b$ est égal à $1$ alors, on peut en déduire que $a\ $ et $\ b$ sont des inverses.
2) Calculons $a^{2}\;;\ b^{2}\ $ et $\ \dfrac{a}{b}.$
En utilisant une propriété des identités remarquables, on trouve :
$\begin{array}{rcl} a^{2}&=&\left(5-2\sqrt{6}\right)^{2}\\\\&=&(5)^{2}-2\times 5\times 2\sqrt{6}+(2\sqrt{6})^{2}\\\\&=&25-20\sqrt{6}+(4\times 6)\\\\&=&25-20\sqrt{6}+24\\\\&=&49-20\sqrt{6}\end{array}$
Ainsi, $\boxed{a^{2}=49-20\sqrt{6}}$
En utilisant une propriété des identités remarquables, on a :
$\begin{array}{rcl} b^{2}&=&\left(5+2\sqrt{6}\right)^{2}\\\\&=&(5)^{2}+2\times 5\times 2\sqrt{6}+(2\sqrt{6})^{2}\\\\&=&25+20\sqrt{6}+(4\times 6)\\\\&=&25+20\sqrt{6}+24\\\\&=&49+20\sqrt{6}\end{array}$
D'où, $\boxed{b^{2}=49+20\sqrt{6}}$
Soit : $\dfrac{a}{b}=\dfrac{5-2\sqrt{6}}{5+2\sqrt{6}}$
Alors, en rendant rationnel le dénominateur puis en calculant, on trouve :
$\begin{array}{rcl}\dfrac{a}{b}&=&\dfrac{5-2\sqrt{6}}{5+2\sqrt{6}}\\\\&=&\dfrac{(5-2\sqrt{6})(5-2\sqrt{6})}{(5+2\sqrt{6})(5-2\sqrt{6})}\\\\&=&\dfrac{(5-2\sqrt{6})^{2}}{(5)^{2}-(2\sqrt{6})^{2}}\\\\&=&\dfrac{49-20\sqrt{6}}{25-(4\times 6)}\\\\&=&\dfrac{49-20\sqrt{6}}{25-24}\\\\&=&\dfrac{49-20\sqrt{6}}{1}\\\\&=&49-20\sqrt{6}\end{array}$
D'où, $\boxed{\dfrac{a}{b}=49-20\sqrt{6}}$
3) Vérifions que $\dfrac{a}{b}+\dfrac{b}{a}$ est un entier naturel.
En réduisant au même dénominateur, on trouve :
$\begin{array}{rcl} \dfrac{a}{b}+\dfrac{b}{a}&=&\dfrac{a\times a}{a\times b}+\dfrac{b\times b}{a\times b}\\\\&=&\dfrac{a^{2}}{a\times b}+\dfrac{b^{2}}{a\times b}\\\\&=&\dfrac{a^{2}+b^{2}}{a\times b}\end{array}$
Donc, $\boxed{\dfrac{a}{b}+\dfrac{b}{a}=\dfrac{a^{2}+b^{2}}{ab}}$
En remplaçant ensuite $a^{2}\;;\ a^{2}\ $ et $\ a\times b$ par leur valeur, on obtient :
$\begin{array}{rcl} \dfrac{a}{b}+\dfrac{b}{a}&=&\dfrac{a^{2}+b^{2}}{a\times b}\\\\&=&\dfrac{49-20\sqrt{6}+49+20\sqrt{6}}{1}\\\\&=&98\end{array}$
D'où, $\boxed{\dfrac{a}{b}+\dfrac{b}{a}=98\quad\text{qui est un entier naturel}}$
Par conséquent, $\dfrac{a}{b}+\dfrac{b}{a}$ est un entier naturel.
4) Soit $X=\sqrt{49-20\sqrt{6}}\ $ et $\ Y=\sqrt{49+20\sqrt{6}}$
Écrivons $X\ $ et $\ Y$ avec un seul radical.
D'après le résultat de la question $2)$, on a : $\left(5-2\sqrt{6}\right)^{2}=49-20\sqrt{6}$
Donc, dans l'expression de $X$, en remplaçant $49-20\sqrt{6}$ par $\left(5-2\sqrt{6}\right)^{2}$, on obtient :
$\begin{array}{rcl} X&=&\sqrt{49-20\sqrt{6}}\\\\&=&\sqrt{\left(5-2\sqrt{6}\right)^{2}}\\\\&=&\left|5-2\sqrt{6}\right|\end{array}$
Cherchons alors le signe de $(5-2\sqrt{6}).$
Pour cela, comparons $5\ $ et $\ 2\sqrt{6}.$
Comme ces deux nombres sont positifs alors, comparons leur carré.
On a : $(5)^{2}=25\ $ et $\ (2\sqrt{6})^{2}=24$
Comme $25$ est plus grand que $24$ alors, $5>2\sqrt{6}.$
D'où, $5-2\sqrt{6}>0$
Ainsi, $\left|5-2\sqrt{6}\right|=5-2\sqrt{6}.$
Par conséquent, $\boxed{X=5-2\sqrt{6}}$
De la même manière, on a : $\left(5+2\sqrt{6}\right)^{2}=49+20\sqrt{6}$
Donc, dans l'expression de $Y$, en remplace $49+20\sqrt{6}$ par $\left(5+2\sqrt{6}\right)^{2}.$
Ce qui donne alors :
$\begin{array}{rcl} Y&=&\sqrt{49+20\sqrt{6}}\\\\&=&\sqrt{\left(5+2\sqrt{6}\right)^{2}}\\\\&=&\left|5+2\sqrt{6}\right|\\\\&=&5+2\sqrt{6}\end{array}$
D'où, $\boxed{Y=5+2\sqrt{6}}$
Exercice 32
On considère l'expression ci-dessous :
$$H(x)=4\left(x+\sqrt{3}\right)^{2}-4\sqrt{3}\left(x+\sqrt{3}\right)+3$$
1) Développons, réduisons et ordonnons $H(x).$
Soit alors :
$\begin{array}{rcl} H(x)&=&4\left(x+\sqrt{3}\right)^{2}-4\sqrt{3}\left(x+\sqrt{3}\right)+3\\\\&=&4\left(x^{2}+2\times\sqrt{3}\times x+(\sqrt{3})^{2}\right)-4\sqrt{3}\times x-4\sqrt{3}\times\sqrt{3}+3\\\\&=&4\left(x^{2}+2\sqrt{3}x+3\right)-4\sqrt{3}x-4\times 3+3\\\\&=&4x^{2}+8\sqrt{3}x+12-4\sqrt{3}x-12+3\\\\&=&4x^{2}+4\sqrt{3}x+3\end{array}$
Ainsi, $\boxed{H(x)=4x^{2}+4\sqrt{3}x+3}$
2) Déduisons-en une factorisation de $H(x).$
D'après le résultat de la question $1)\;,\ H(x)$ est de la forme : $a^{2}+2ab+b^{2}$ avec ; $a=2x\ $ et $\ b=\sqrt{3}.$
Or, on sait que :
$$a^{2}+2ab+b^{2}=(a+b)^{2}$$
Donc, en utilisant cette propriété des identités remarquables, on a :
$$4x^{2}+4\sqrt{3}x+3=(2x+\sqrt{3})^{2}$$
D'où, $\boxed{H(x)=(2x+\sqrt{3})^{2}}$
Exercice 33
On donne :
$a=\dfrac{2-\sqrt{3}}{5+\sqrt{3}}$
$b=3\sqrt{18}+\sqrt{128}-\sqrt{338}$
$c=\sqrt{2}-3.$
1) Rendons rationnel le dénominateur de $a.$
Soit $5-\sqrt{3}$ l'expression conjuguée du dénominateur de $a.$
Alors, on a :
$\begin{array}{rcl} a&=&\dfrac{2-\sqrt{3}}{5+\sqrt{3}}\\\\&=&\dfrac{(2-\sqrt{3})(5-\sqrt{3})}{(5+\sqrt{3})(5-\sqrt{3})}\\\\&=&\dfrac{2\times 5-2\sqrt{3}-5\sqrt{3}-\sqrt{3}\times(-\sqrt{3})}{(5)^{2}-(\sqrt{3})^{2}}\\\\&=&\dfrac{10-7\sqrt{3}+3}{25-3}\\\\&=&\dfrac{13-7\sqrt{3}}{22}\end{array}$
D'où, $\boxed{a=\dfrac{13-7\sqrt{3}}{22}}$
2) Simplifions $b.$
On a :
$18=9\times 2$
$128=64\times 2$
$338=13^{2}\times 2$
Donc, en remplaçant dans l'expression de $b$, on obtient :
$\begin{array}{rcl} b&=&3\sqrt{18}+\sqrt{128}-\sqrt{338}\\\\&=&3\sqrt{9\times 2}+\sqrt{64\times 2}-\sqrt{13^{2}\times 2}\\\\&=&3\sqrt{9}\times\sqrt{2}+\sqrt{64}\times\sqrt{2}-\sqrt{13^{2}}\times\sqrt{2}\\\\&=&3\times 3\times\sqrt{2}+8\times\sqrt{2}-13\times\sqrt{2}\\\\&=&9\sqrt{2}+8\sqrt{2}-13\sqrt{2}\\\\&=&4\sqrt{2}\end{array}$
Ainsi, $\boxed{b=4\sqrt{2}}$
3) Calculons $c^{2}.$
On a :
$\begin{array}{rcl} c^{2}&=&\left(\sqrt{2}-3\right)^{2}\\\\&=&(\sqrt{2})^{2}-2\times 3\times \sqrt{2}+(3)^{2}\\\\&=&2-6\sqrt{2}+9\\\\&=&11-6\sqrt{2}\end{array}$
D'où, $\boxed{c^{2}=11-6\sqrt{2}}$
Déduisons-en que $p=\dfrac{\sqrt{5}-\sqrt{8}}{3\sqrt{5}-6\sqrt{2}}$ est un rationnel que l'on déterminera.
On a :
$\begin{array}{rcl} p&=&\dfrac{\sqrt{5}-\sqrt{8}}{3\sqrt{5}-6\sqrt{2}}\\\\&=&\dfrac{\sqrt{5}-\sqrt{4\times 2}}{3\sqrt{5}-6\sqrt{2}}\\\\&=&\dfrac{\sqrt{5}-\sqrt{4}\times\sqrt{2}}{3(\sqrt{5}-2\sqrt{2})}\\\\&=&\dfrac{(\sqrt{5}-2\sqrt{2})}{3(\sqrt{5}-2\sqrt{2})}\\\\&=&\dfrac{1}{3}\end{array}$
D'où, $\boxed{p=\dfrac{1}{3}\quad\text{qui est un nombre rationnel}}$
Exercice 34
Écrivons le plus simplement possible les expressions ci-dessous :
$$G=\sqrt{76-2\sqrt{37-\sqrt{\dfrac{21}{25}+\dfrac{1}{25}\times\sqrt{6+\sqrt{103-2\sqrt{\dfrac{9}{4}}}}}}}$$
En calculant de la droite vers la gauche, on obtient :
$\begin{array}{rcl} G&=&\sqrt{76-2\sqrt{37-\sqrt{\dfrac{21}{25}+\dfrac{1}{25}\times\sqrt{6+\sqrt{103-2\sqrt{\dfrac{9}{4}}}}}}}\\\\&=&\sqrt{76-2\sqrt{37-\sqrt{\dfrac{21}{25}+\dfrac{1}{25}\times\sqrt{6+\sqrt{103-2\times\dfrac{\sqrt{9}}{\sqrt{4}}}}}}}\\\\&=&\sqrt{76-2\sqrt{37-\sqrt{\dfrac{21}{25}+\dfrac{1}{25}\times\sqrt{6+\sqrt{103-2\times\dfrac{3}{2}}}}}}\\\\&=&\sqrt{76-2\sqrt{37-\sqrt{\dfrac{21}{25}+\dfrac{1}{25}\times\sqrt{6+\sqrt{103-3}}}}}\\\\&=&\sqrt{76-2\sqrt{37-\sqrt{\dfrac{21}{25}+\dfrac{1}{25}\times\sqrt{6+\sqrt{100}}}}}\\\\&=&\sqrt{76-2\sqrt{37-\sqrt{\dfrac{21}{25}+\dfrac{1}{25}\times\sqrt{6+10}}}}\\\\&=&\sqrt{76-2\sqrt{37-\sqrt{\dfrac{21}{25}+\dfrac{1}{25}\times\sqrt{16}}}}\\\\&=&\sqrt{76-2\sqrt{37-\sqrt{\dfrac{21}{25}+\dfrac{1}{25}\times 4}}}\\\\&=&\sqrt{76-2\sqrt{37-\sqrt{\dfrac{21}{25}+\dfrac{4}{25}}}}\\\\&=&\sqrt{76-2\sqrt{37-\sqrt{\dfrac{25}{25}}}}\\\\&=&\sqrt{76-2\sqrt{37-\sqrt{1}}}\\\\&=&\sqrt{76-2\sqrt{37-1}}\\\\&=&\sqrt{76-2\sqrt{36}}\\\\&=&\sqrt{76-2\times 6}\\\\&=&\sqrt{76-12}\\\\&=&\sqrt{64}\\\\&=&8\end{array}$
D'où, $\boxed{G=8}$
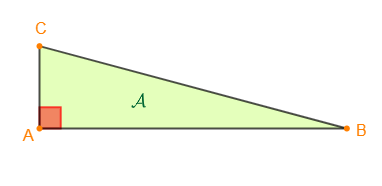
On donne un triangle $ABC$ rectangle en $A$ tel que $AC=\sqrt{3}-1\ $ et $\ BC=2\sqrt{2}.$
1) Calculons $AB^{2}$, déduisons-en que $AB=\sqrt{3}+1$ puis l'aire du triangle $ABC.$
Comme le triangle $ABC$ est rectangle en $A$ alors, d'après le théorème de Pythagore, on a :
$$AB^{2}+AC^{2}=BC^{2}$$
Ce qui entraine : $AB^{2}=BC^{2}-AC^{2}$
En remplaçant $AC^{2}\ $ et $\ BC^{2}$ par leur valeur, on obtient :
$\begin{array}{rcl} AB^{2}&=&BC^{2}-AC^{2}\\\\&=&(2\sqrt{2})^{2}-(\sqrt{3}-1)^{2}\\\\&=&(4\times 2)-\left((\sqrt{3})^{2}-2\times 1\times\sqrt{3}+(1)^{2}\right)\\\\&=&8-(3-2\sqrt{3}+1)\\\\&=&8-(4-2\sqrt{3})\\\\&=&8-4+2\sqrt{3}\\\\&=&4+2\sqrt{3}\end{array}$
Donc, $\boxed{AB^{2}=4+2\sqrt{3}}$
Déduisons-en que $AB=\sqrt{3}+1$
Comme $AB^{2}=4+2\sqrt{3}$ alors, on a : $\sqrt{AB^{2}}=\sqrt{4+2\sqrt{3}}$
Or, on sait que : $4+2\sqrt{3}=(\sqrt{3}+1)^{2}$
Donc, en remplaçant, on obtient : $\sqrt{AB^{2}}=\sqrt{(\sqrt{3}+1)^{2}}$
Ce qui donne : $|AB|=\left|\sqrt{3}+1\right|$
Par ailleurs, on sait que $AB$ est la longueur d'un côté du triangle donc, $AB$ est positive.
D'où, $|AB|=AB$
De plus, la somme de deux nombres positifs est un nombre positif donc, $\sqrt{3}+1>0$
Ainsi, $\left|\sqrt{3}+1\right|=\sqrt{3}+1$
Par conséquent, $\boxed{AB=\sqrt{3}+1}$
Calculons l'aire $\mathcal{A}$ de ce triangle.
On a :
$\begin{array}{rcl}\mathcal{A}&=&\dfrac{AB\times AC}{2}\\\\&=&\dfrac{(\sqrt{3}+1)\times(\sqrt{3}-1)}{2}\\\\&=&\dfrac{(\sqrt{3})^{2}-(1)^{2}}{2}\\\\&=&\dfrac{3-1}{2}\\\\&=&\dfrac{2}{2}\\\\&=&1\end{array}$
Ainsi, $\boxed{\mathcal{A}=1}$
2) Calculons $\dfrac{1}{AC}$ sans radical au dénominateur.
Soit : $\dfrac{1}{AC}=\dfrac{1}{\sqrt{3}-1}$
Donc, rendons rationnel le dénominateur de $\dfrac{1}{\sqrt{3}-1}$
Comme $\sqrt{3}+1$ est l'expression conjuguée de $\sqrt{3}-1$ alors, on a :
$\begin{array}{rcl}\dfrac{1}{AC}&=&\dfrac{1}{\sqrt{3}-1}\\\\&=&\dfrac{1\times(\sqrt{3}+1)}{(\sqrt{3}-1)(\sqrt{3}+1)}\\\\&=&\dfrac{\sqrt{3}+1}{(\sqrt{3})^{2}-(1)^{2}}\\\\&=&\dfrac{\sqrt{3}+1}{3-1}\\\\&=&\dfrac{\sqrt{3}+1}{2}\end{array}$
Ainsi, $\boxed{\dfrac{1}{AC}=\dfrac{\sqrt{3}+1}{2}}$
Déduisons-en un encadrement de $\dfrac{1}{AC}$ d'amplitude $0.01$
On sait que : $1.73<\sqrt{3}<1.74$
Alors, ajoutons $1$ à chaque membre de l'inégalité.
On obtient :
$$1.73+1<\sqrt{3}+1<1.74+1$$
Ce qui donne : $2.73<\sqrt{3}+1<2.74$
Divisons ensuite chaque membre de cette dernière inégalité par le même nombre $2.$
On trouve alors :
$$\dfrac{2.73}{2}<\dfrac{\sqrt{3}+1}{2}<\dfrac{2.74}{2}$$
Ce qui est équivalent à : $1.36<\dfrac{\sqrt{3}+1}{2}<1.37$
D'où, un encadrement de $\dfrac{1}{AC}$ d'amplitude $0.01$ est donné par :
$$\boxed{1.36<\dfrac{1}{AC}<1.37}$$
Exercice 35
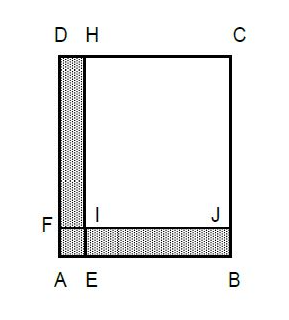
$ABCD\ $ et $\ CHIJ$ sont des carrés de côtés respectifs : $5\sqrt{3}-1\ $ et $\ \sqrt{27}.$ (Voir figure ci-dessous)
1) Calculons l'aire du carré $ABCD.$
L'aire $\mathcal{A}_{_{(ABCD)}}$ est donnée par :
$$\mathcal{A}_{_{(ABCD)}}=(\text{côté})^{2}$$
Comme son côté est de longueur $5\sqrt{3}-1$ alors, on a :
$\begin{array}{rcl} \mathcal{A}_{_{(ABCD)}}&=&(\text{côté})^{2}\\\\&=&(5\sqrt{3}-1)^{2}\\\\&=&(5\sqrt{3})^{2}-2\times 1\times 5\sqrt{3}+(1)^{2}\\\\&=&(25\times 3)-10\sqrt{3}+1\\\\&=&75-10\sqrt{3}+1\\\\&=&76-10\sqrt{3}\end{array}$
Ainsi, $\boxed{\mathcal{A}_{_{(ABCD)}}=76-10\sqrt{3}}$
2) Calculons l'aire du carré $CHIJ.$
L'aire $\mathcal{A}_{_{(CHIJ)}}$ est donnée par :
$$\mathcal{A}_{_{(ABCD)}}=(\text{côté})^{2}$$
Or, le côté de ce carré a pour longueur $\sqrt{27}$ donc, on a :
$\begin{array}{rcl} \mathcal{A}_{_{(CHIJ)}}&=&(\text{côté})^{2}\\\\&=&(\sqrt{27})^{2}\\\\&=&27\end{array}$
D'où, $\boxed{\mathcal{A}_{_{(CHIJ)}}=27}$
3) Calculons la longueur $AE.$
On a : $AE=AB-EB$
En observant la figure, on remarque que $EB=IJ=\sqrt{27}$
De plus, on sait que $AB=5\sqrt{3}-1$
Donc, en remplaçant $AB$ par $5\sqrt{3}-1\ $ et $\ EB$ par $\sqrt{27}$, on obtient :
$\begin{array}{rcl} AE&=&AB-EB\\\\&=&5\sqrt{3}-1-\sqrt{27}\\\\&=&5\sqrt{3}-1-\sqrt{9\times 3}\\\\&=&5\sqrt{3}-1-\sqrt{9}\times\sqrt{3}\\\\&=&5\sqrt{3}-1-3\sqrt{3}\\\\&=&2\sqrt{3}-1\end{array}$
Ainsi, $\boxed{AE=2\sqrt{3}-1}$
4) Calculons le périmètre du rectangle $CDFJ.$
Le périmètre $\mathcal{P}_{_{(CDFJ)}}$ du rectangle $CDFJ$ est donné par :
$$\mathcal{P}_{_{(CDFJ)}}=2\times(CD+CJ)$$
Comme $CD=5\sqrt{3}-1\ $ et $\ CJ=\sqrt{27}$ alors, on a :
$\begin{array}{rcl} \mathcal{P}_{_{(CDFJ)}}&=&2\times(CD+CJ)\\\\&=&2\times(5\sqrt{3}-1+\sqrt{27})\\\\&=&2\times(5\sqrt{3}-1+\sqrt{9\times 3})\\\\&=&2\times(5\sqrt{3}-1+\sqrt{9}\times\sqrt{3})\\\\&=&2\times(5\sqrt{3}-1+3\sqrt{3})\\\\&=&2\times(8\sqrt{3}-1)\\\\&=&16\sqrt{3}-2\end{array}$
D'où, $\boxed{\mathcal{P}_{_{(CDFJ)}}=16\sqrt{3}-2}$
5) Calculons l'aire de la surface coloriée.
En observant la figure, on remarque l'aire de la surface coloriée est égale à la différence entre l'aire du carré $ABCD$ et celle du carré $CHIJ.$
Ainsi, on a :
$\begin{array}{rcl} \mathcal{A}_{_{(\text{partie coloriée})}}&=&\mathcal{A}_{_{(ABCD)}}-\mathcal{A}_{_{(CHIJ)}}\\\\&=&76-10\sqrt{3}-27\\\\&=&49-10\sqrt{3}\end{array}$
D'où, $\boxed{\mathcal{A}_{_{(\text{partie coloriée})}}=49-10\sqrt{3}}$
Exercice 36
1) Écrivons les expressions $x\ $ et $\ y$ ci-dessous sous la forme $a\sqrt{b}$ où $a\ $ et $\ b$ sont des entiers positifs.
a) Soit : $x=2\sqrt{50}-3\sqrt{18}+\sqrt{200}-\sqrt{2}.$
Alors, on a :
$\begin{array}{rcl} x&=&2\sqrt{50}-3\sqrt{18}+\sqrt{200}-\sqrt{2}\\\\&=&2\sqrt{25\times 2}-3\sqrt{9\times 2}+\sqrt{100\times 2}-\sqrt{2}\\\\&=&2\sqrt{25}\times\sqrt{2}-3\sqrt{9}\times\sqrt{2}+\sqrt{100}\times\sqrt{2}-\sqrt{2}\\\\&=&2\times 5\times\sqrt{2}-3\times 3\times\sqrt{2}+10\times\sqrt{2}-\sqrt{2}\\\\&=&10\sqrt{2}-9\sqrt{2}+10\sqrt{2}-\sqrt{2}\\\\&=&10\sqrt{2}\end{array}$
Donc, $\boxed{x=10\sqrt{2}}$
b) Soit : $y=\sqrt{20}+\sqrt{80}-\dfrac{\sqrt{32}}{\sqrt{12}}\times\sqrt{48}.$
Alors, on a :
$\begin{array}{rcl} y&=&\sqrt{20}+\sqrt{80}-\dfrac{\sqrt{32}}{\sqrt{12}}\times\sqrt{48}\\\\&=&\sqrt{4\times 5}+\sqrt{16\times 5}-\dfrac{\sqrt{16\times 2}}{\sqrt{4\times 3}}\times\sqrt{16\times 3}\\\\&=&\sqrt{4}\times\sqrt{5}+\sqrt{16}\times\sqrt{5}-\dfrac{\sqrt{16}\times\sqrt{2}}{\sqrt{4}\times\sqrt{3}}\times\sqrt{16}\times\sqrt{3}\\\\&=&2\times\sqrt{5}+4\times\sqrt{5}-\dfrac{4\times\sqrt{2}}{2\times\sqrt{3}}\times 4\times\sqrt{3}\\\\&=&2\sqrt{5}+4\sqrt{5}-\dfrac{16\sqrt{2}}{2}\\\\&=&6\sqrt{5}-8\sqrt{2}\end{array}$
D'où, $\boxed{y=6\sqrt{5}-8\sqrt{2}}$
2) On donne les réels $m=1-2\sqrt{3}\ $ et $\ n=1+\sqrt{12}$
a) Sans calculer $m^{2}\ $ et $\ n^{2}$ montrons que $m+n\;,\ m\times n$ sont des entiers relatifs.
On a :
$\begin{array}{rcl} m+n&=&1-2\sqrt{3}+1+\sqrt{12}\\\\&=&2-2\sqrt{3}+\sqrt{4\times 3}\\\\&=&2-2\sqrt{3}+\sqrt{4}\times\sqrt{3}\\\\&=&2-2\sqrt{3}+2\sqrt{3}\\\\&=&2\end{array}$
Donc, $\boxed{m+n=2\quad\text{qui est un entier relatif}}$
On a :
$\begin{array}{rcl} m\times n&=&(1-2\sqrt{3})(1+\sqrt{12})\\\\&=&(1-2\sqrt{3})(1+\sqrt{4}\times\sqrt{3})\\\\&=&(1-2\sqrt{3})(1+2\sqrt{3})\\\\&=&(1)^{2}-(2\sqrt{3})^{2}\\\\&=&1-(4\times 3)\\\\&=&1-12\\\\&=&-11\end{array}$
D'où, $\boxed{m\times n=-11\quad\text{qui est un entier relatif}}$
b) Déduisons-en que $m^{2}+n^{2}$ est un entier relatif.
En effet, d'après la propriété des identités remarquables, on a :
$$(m+n)^{2}=m^{2}+2\times(m\times n)+n^{2}$$
Ce qui entraine : $m^{2}+n^{2}=(m+n)^{2}-2\times m\times n$
Ainsi, on a :
$\begin{array}{rcl} m^{2}+n^{2}&=&(m+n)^{2}-2\times(m\times n)\\\\&=&(2)^{2}-2\times(-11)\\\\&=&4+22\\\\&=&26\end{array}$
D'où, $\boxed{m^{2}+n^{2}=26\quad\text{qui est un entier relatif}}$
3) On pose $p=\dfrac{m}{n}.$
Rendons rationnel le dénominateur de $p.$
Soit : $p=\dfrac{1-2\sqrt{3}}{1+\sqrt{12}}$ alors, on a :
$\begin{array}{rcl} p&=&\dfrac{1-2\sqrt{3}}{1+\sqrt{12}}\\\\&=&\dfrac{(1-2\sqrt{3})(1-\sqrt{12})}{(1+\sqrt{12})(1-\sqrt{12})}\\\\&=&\dfrac{(1-2\sqrt{3})(1-2\sqrt{3})}{(1)^{2}-(\sqrt{12})^{2}}\\\\&=&\dfrac{(1-2\sqrt{3})^{2}}{1-12}\\\\&=&\dfrac{(1-2\sqrt{3})^{2}}{-11}\\\\&=&-\dfrac{(1-2\sqrt{3})^{2}}{11}\end{array}$
D'où, $\boxed{p=-\dfrac{(1-2\sqrt{3})^{2}}{11}}$
Exercice 37
On donne : $A=\left(\sqrt{5}-\sqrt{3}\right)^{2}\ $ et $\ B=x^{2}-7x+10.$
1) Calculons $A$ puis, déduisons-en l'expression simplifiée du nombre : $C=\dfrac{1}{2}\left(\sqrt{5}-\sqrt{8-2\sqrt{15}}\right).$
$-\ $ calcul de $A$
En développant, on obtient :
$\begin{array}{rcl} A&=&\left(\sqrt{5}-\sqrt{3}\right)^{2}\\\\&=&(\sqrt{5})^{2}-2\times\sqrt{5}\times\sqrt{3}+(\sqrt{3})^{2}\\\\&=&5-2\times\sqrt{5\times 3}+3\\\\&=&8-2\sqrt{15}\end{array}$
D'où, $\boxed{A=8-2\sqrt{15}}$
$-\ $ simplification de $C$
Dans l'expression de $C$, en remplaçant $8-2\sqrt{15}$ par $\left(\sqrt{5}-\sqrt{3}\right)^{2}$, on obtient :
$\begin{array}{rcl} C&=&\dfrac{1}{2}\left(\sqrt{5}-\sqrt{8-2\sqrt{15}}\right)\\\\&=&\dfrac{1}{2}\left(\sqrt{5}-\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^{2}}\right)\\\\&=&\dfrac{1}{2}\left(\sqrt{5}-\left|\sqrt{5}-\sqrt{3}\right|\right)\end{array}$
Cherchons alors le signe de $(\sqrt{5}-\sqrt{3}$
Pour cela, comparons $\sqrt{5}\ $ et $\ \sqrt{3}.$
Comme ces deux nombres sont positifs alors, comparons leur carré.
On a : $(\sqrt{5})^{2}=5\ $ et $\ (\sqrt{3})^{2}=3$
Comme $5$ est plus grand que $3$ alors, $\sqrt{5}>\sqrt{3}.$
Donc, $\sqrt{5}-\sqrt{3}>0$
D'où, $\left|\sqrt{5}-\sqrt{3}\right|=\sqrt{5}-\sqrt{3}.$
Par conséquent,
$\begin{array}{rcl} C&=&\dfrac{1}{2}\left(\sqrt{5}-\left|\sqrt{5}-\sqrt{3}\right|\right)\\\\&=&\dfrac{1}{2}\left(\sqrt{5}-(\sqrt{5}-\sqrt{3})\right)\\\\&=&\dfrac{1}{2}\left(\sqrt{5}-\sqrt{5}+\sqrt{3}\right)\\\\&=&\dfrac{1}{2}\times\sqrt{3}\end{array}$
Ainsi, $\boxed{C=\dfrac{\sqrt{3}}{2}}$
2) Calculons $B$ pour $x=\sqrt{2}.$
Pour cela, on remplace $x$ par $\sqrt{2}$, dans l'expression de $B(x).$
Alors, on a :
$\begin{array}{rcl} B(\sqrt{2})&=&(\sqrt{2})^{2}-7\times\sqrt{2}+10\\\\&=&2-7\sqrt{2}+10\\\\&=&12-7\sqrt{2}\end{array}$
D'où, $\boxed{B(\sqrt{2})=12-7\sqrt{2}}$
3) Donnons un encadrement du nombre $D=12-7\sqrt{2}$ sachant que $1.414<\sqrt{2}<1.415$ puis, déduisons-en la valeur approchée de $D$ à $10^{-2}$ près par défaut.
On sait que : $1.414<\sqrt{2}<1.415$
Alors, multiplions chaque membre de l'inégalité par le même nombre $-7$ en changeant le sens des inégalités.
On obtient :
$$-7\times 1.414>-7\sqrt{2}>-7\times 1.415$$
Ce qui donne : $-9.898>-7\sqrt{2}>-9.905$
En ajoutant $12$ à chaque membre de cette dernière l'inégalité, on obtient :
$$12-9.898>12-7\sqrt{2}>12-9.905$$
Donc, on a : $2.102>12-7\sqrt{2}>2.095$
Ce qui est équivalent à : $2.095<12-7\sqrt{2}<2.102$
D'où, un encadrement de $D$ à $10^{-2}$ près est donné par :
$$\boxed{2.09<D<2.10}$$
Par conséquent, la valeur approchée de $D$ à $10^{-2}$ près par défaut est égale à $2.09$
Auteur:
Diny Faye
Commentaires
Anonyme (non vérifié)
jeu, 04/11/2019 - 01:07
Permalien
Où sont les autres solutions
Dame gaye (non vérifié)
lun, 11/11/2019 - 19:05
Permalien
C´est formidable pour les
Diack (non vérifié)
jeu, 02/20/2020 - 20:36
Permalien
Je veux les autres solutions
Karamokho Danfakha (non vérifié)
ven, 06/12/2020 - 11:00
Permalien
Racine carré
Karamokho Danfakha (non vérifié)
ven, 06/12/2020 - 11:04
Permalien
Racine carré
Traoré (non vérifié)
mar, 08/18/2020 - 23:56
Permalien
J'aime beaucoup ce site les
Anonyme (non vérifié)
lun, 09/07/2020 - 17:03
Permalien
Formidable
Gisèle (non vérifié)
dim, 12/27/2020 - 22:22
Permalien
Être dans le groupe
Gisèle (non vérifié)
dim, 12/27/2020 - 22:22
Permalien
Être dans le groupe
Anonyme (non vérifié)
mer, 01/06/2021 - 19:23
Permalien
La correction des autres
Anonyme (non vérifié)
sam, 01/23/2021 - 18:55
Permalien
Nous aimons beaucoup ce site
Aissatou diop (non vérifié)
dim, 05/16/2021 - 22:50
Permalien
C formidable
Aissatou diop (non vérifié)
dim, 05/16/2021 - 22:50
Permalien
C formidable
Anonyme (non vérifié)
jeu, 11/04/2021 - 07:39
Permalien
Intéressant
Anonyme (non vérifié)
lun, 03/14/2022 - 15:35
Permalien
Où sont les autres
Anonyme (non vérifié)
lun, 03/14/2022 - 15:35
Permalien
Où sont les autres
Philippe TCHAM (non vérifié)
mar, 06/28/2022 - 23:58
Permalien
Appreciation
Anonyme (non vérifié)
jeu, 12/01/2022 - 21:55
Permalien
waouh c est formidable ce me
Ajouter un commentaire