Produit scalaire - 2nd
Classe:
Seconde
I. Définitions
I.1 Définition 1
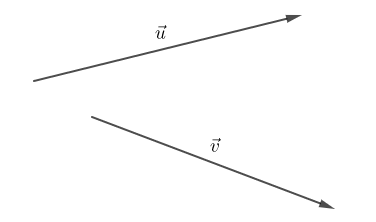
Soient $\vec{u}\ $ et $\ \vec{v}$ deux vecteurs non nuls, $A$ un point du plan. Il existe deux points $B\ $ et $\ C$ tels que $\overrightarrow{AB}=\vec{u}\ $ et $\ \overrightarrow{AC}=\vec{v}$
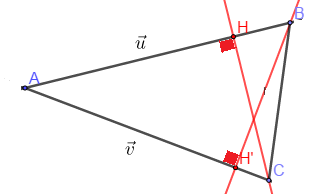
On appelle produit scalaire de $\vec{u}\ $ et $\ \vec{v}$ le réel noté $$\vec{u}\cdot\vec{v}=\overrightarrow{AB}\cdot\overrightarrow{AC}=\overline{AB}\times\overline{AH}=\overline{AH'}\times\overline{AC}$$ où $H$ est le projeté orthogonal de $C$ sur $(AB)$ et $H'$ est le projeté orthogonal de $B$ sur $(AC).$
I.2 Définition 2
$\overrightarrow{AB}\cdot\overrightarrow{AC}=||\overrightarrow{AB}||\times||\overrightarrow{AC}||\times\cos(\overrightarrow{AB},\ \overrightarrow{AC})$
En effet
$\overrightarrow{AB}\cdot\overrightarrow{AC}=\overline{AB}\times\overline{AC}=AB.AC=||\overrightarrow{AB}||\times||\overrightarrow{AC}||\times\underbrace{\cos(\overrightarrow{AB},\ \overrightarrow{AC})}_{=1}$
$\overrightarrow{AB}\cdot\overrightarrow{AC}=\overline{AB}\times\overline{AC}=-AB.AC=||\overrightarrow{AB}||\times||\overrightarrow{AC}||\times\underbrace{\cos(\overrightarrow{AB},\ \overrightarrow{AC})}_{=-1}$
$\overrightarrow{AB}\cdot\overrightarrow{AC}=\overline{AB}\times\overline{AA}=0=||\overrightarrow{AB}||\times||\overrightarrow{AC}||\times\underbrace{\cos(\overrightarrow{AB},\ \overrightarrow{AC})}_{=0}$
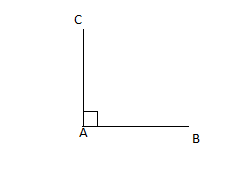
$\overrightarrow{AB}\cdot\overrightarrow{AC}=\overline{AB}\times\overline{AH}$
Or, $\cos(\overrightarrow{AB},\ \overrightarrow{AC})=\dfrac{\overline{AH}}{\overline{AC}}$ donc, $\overline{AH}=AC.\cos(\overrightarrow{AB},\ \overrightarrow{AC})$
Par suite, $\overrightarrow{AB}\cdot\overrightarrow{AC}=AB\times AC\times\cos(\overrightarrow{AB},\ \overrightarrow{AC})$
D'où, $\overrightarrow{AB}\cdot\overrightarrow{AC}=||\overrightarrow{AB}||\times||\overrightarrow{AC}||\times\cos(\overrightarrow{AB},\ \overrightarrow{AC})$
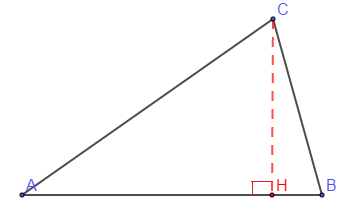
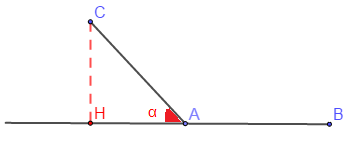
$\overrightarrow{AB}\cdot\overrightarrow{AC}=\overline{AB}\times\overline{AH}=-AB\times AH$
Or, $\cos(\overrightarrow{AB},\ \overrightarrow{AC})=\dfrac{\overline{AH}}{\overline{AC}}=\cos(\pi-(\overrightarrow{AB},\ \overrightarrow{AC}))=-\cos(\overrightarrow{AB},\ \overrightarrow{AC})$
Donc, $\overline{AH}=-AC.\cos(\overrightarrow{AB},\ \overrightarrow{AC})$
Par suite, $\overrightarrow{AB}\cdot\overrightarrow{AC}=AB\times AC\times\cos(\overrightarrow{AB},\ \overrightarrow{AC})$
D'où, $\overrightarrow{AB}\cdot\overrightarrow{AC}=||\overrightarrow{AB}||\times||\overrightarrow{AC}||\times\cos(\overrightarrow{AB},\ \overrightarrow{AC})$
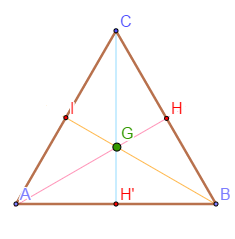
Activité
Soit $ABC$ un triangle équilatéral de coté 4, de centre $G$ et on désigne par $I$ le milieu du coté $[AC].$
Calculer les produits scalaires ci-dessous.
$\overrightarrow{IB}\cdot\overrightarrow{AC}\;;\ \overrightarrow{IB}\cdot\overrightarrow{CI}\;;\ \overrightarrow{IG}\cdot\overrightarrow{AI}\;;\ \overrightarrow{AB}\cdot\overrightarrow{AC}$
$\overrightarrow{BI}\cdot\overrightarrow{BI}\;;\ \overrightarrow{AB}\cdot\overrightarrow{AG}\;;\ \overrightarrow{GB}\cdot\overrightarrow{GC}$
Résolution
$\overrightarrow{IB}\cdot\overrightarrow{AC}=IB\times AC\times\cos(\overrightarrow{IB}\;,\ \overrightarrow{AC})$ or $\widehat{(\overrightarrow{IB}\;,\ \overrightarrow{AC})}=90^{\circ}$ donc, $\cos(\overrightarrow{IB}\;,\ \overrightarrow{AC})=0$
Ainsi, $\overrightarrow{IB}\cdot\overrightarrow{AC}=IB\times AC\times\cos(\overrightarrow{IB}\;,\ \overrightarrow{AC})=0$
$\overrightarrow{IB}\cdot\overrightarrow{CI}=IB\times CI\times\cos(\overrightarrow{IB}\;,\ \overrightarrow{CI})=0$ car, $(IB)\perp(IC)$
$\overrightarrow{IG}\cdot\overrightarrow{AI}=IG\times AI\times\cos(\overrightarrow{IG}\;,\ \overrightarrow{AI})=0$ car, $(IG)\perp(AI)$
$$\begin{array}{rcl}\overrightarrow{AB}\cdot\overrightarrow{AC}&=&AB\times AC\times\cos(\overrightarrow{AB}\;,\ \overrightarrow{AC})\\ \\ &=&4\times 4\times\cos\left(\dfrac{\pi}{3}\right)\\ \\ &=&4\times 4\times\dfrac{1}{2}\\ \\ &=& 8\end{array}$$
D'où, $\overrightarrow{AB}\cdot\overrightarrow{AC}=8$
$\overrightarrow{BI}\cdot\overrightarrow{BI}=BI^{2}\times\cos(\overrightarrow{BI}\;,\ \overrightarrow{BI})$ or d'après théorème de Pythagore on a $$\begin{array}{rcl} BI^{2}&=&BC^{2}-IC^{2}\\ \\ &=&4^{2}-2^{2}\\ \\ &=&16-4\\ \\&=&12\end{array}$$
D'où $\overrightarrow{BI}\cdot\overrightarrow{BI}=12$
$$\begin{array}{rcl}\overrightarrow{AB}\cdot\overrightarrow{AG}&=&AB\times AG\times\cos(\overrightarrow{AB}\;,\ \overrightarrow{AG})\quad\text{or }\ AG=\dfrac{2}{3}AH\ \text{ et }\ (\overrightarrow{AB}\;,\ \overrightarrow{AG})=\dfrac{(\overrightarrow{AB}\;,\ \overrightarrow{AC})}{2}\\ \\ &=&4\times\dfrac{2}{3}AH\times\cos\left(\dfrac{\pi}{6}\right)\quad\text{or }\ BH=BI\\ \\ &=&4\times\dfrac{2}{3}BI\times\dfrac{\sqrt{3}}{2}\\ \\ &=&4\times\dfrac{2}{3}\times 2\sqrt{3}\times\dfrac{\sqrt{3}}{2}\\ \\&=&8\end{array}$$
D'où, $\overrightarrow{AB}\cdot\overrightarrow{AG}=8$
$$\begin{array}{rcl}\overrightarrow{GB}\cdot\overrightarrow{GC}&=&GB\times GC\times\cos(\overrightarrow{GB}\;,\ \overrightarrow{GC})\quad\text{or }\ (\overrightarrow{GB}\;,\ \overrightarrow{GC})=2(\overrightarrow{AB}\;,\ \overrightarrow{AC})\\ \\ &=&\dfrac{2}{3}BI\times\dfrac{2}{3}BI\times\cos\left(\dfrac{2\pi}{3}\right)\\ \\ &=&\dfrac{4}{9}\times 12\times\left(-\dfrac{1}{2}\right)\ =\ -\dfrac{8}{3}\end{array}$$
D'où, $\overrightarrow{GB}\cdot\overrightarrow{GC}=-\dfrac{8}{3}$
I.3 Propriétés
$\centerdot\ \ \vec{u}\cdot\vec{v}=\vec{v}\cdot\vec{u}$
En effet, $\vec{u}\cdot\vec{v}=||\vec{u}||.||\vec{v}||.\cos(\vec{u},\ \vec{v})$
$\vec{v}\cdot\vec{u}=||\vec{v}||.||\vec{u}||.\cos(\vec{v},\ \vec{u})$, or $(\vec{v},\ \vec{u})=-(\vec{u},\ \vec{v})$
Donc, $\cos(\vec{v},\ \vec{u})=\cos(-(\vec{u},\ \vec{v}))=\cos(\vec{u},\ \vec{v}))$
D'où, $\vec{u}\cdot\vec{v}=\vec{v}\cdot\vec{u}$
$\centerdot\ \ \alpha\in\mathbb{R}, \ \vec{u}\cdot(\alpha\vec{v})=(\alpha\vec{u}\cdot\vec{v})=\alpha(\vec{u}\cdot\vec{v})$
$\centerdot\ \ \alpha, \beta\in\mathbb{R}, \ (\alpha\vec{u})\cdot(\beta\vec{v})=(\vec{u}\cdot\vec{v})(\alpha.\beta)$
$\centerdot\ \ \vec{u}\cdot(\vec{v}+\vec{w})=\vec{u}\cdot\vec{v}+\vec{u}\cdot\vec{w}$
$\centerdot\ \ \vec{u}\neq\vec{0}, \quad \vec{v}\neq\vec{0}, \quad \vec{u}\cdot\vec{v}=0 \quad \Longleftrightarrow\vec{u}\perp\vec{v}$
$\centerdot\ \ ||\vec{u}+\vec{v}||^{2}=||\vec{u}||^{2}+||\vec{v}||^{2}+2\vec{u}\cdot\vec{v}$
$\centerdot\ \ ||\vec{u}-\vec{v}||^{2}=||\vec{u}||^{2}+||\vec{v}||^{2}-2\vec{u}\cdot\vec{v}$
$\centerdot\ \ ||\vec{u}+\vec{v}||^{2}+||\vec{u}-\vec{v}||^{2}=2(||\vec{u}||^{2}+||\vec{u}||^{2})$
$\centerdot\ \ \vec{u}\cdot\vec{u}=||\vec{u}||^{2}$
I.4 Expression du produit scalaire dans une base orthonormé
$(O\;\ \vec{i}\;,\ \vec{j})$ un repère orthonormé direct.
$||\vec{i}||=||\vec{j}||=1$
$\vec{i}\perp\vec{j}$ et $\vec{i}\cdot\vec{j}=0$
$\vec{i}\cdot\vec{i}=||\vec{i}||^{2}=1$ et $\vec{j}\cdot\vec{j}=||\vec{j}||^{2}=1$
Considérons deux vecteurs $\vec{u}\begin{pmatrix}
x\\
y
\end{pmatrix}$ et $\vec{v}\begin{pmatrix}
x'\\
y'
\end{pmatrix}$ dans cette base.
x\\
y
\end{pmatrix}$ et $\vec{v}\begin{pmatrix}
x'\\
y'
\end{pmatrix}$ dans cette base.
On a : $\vec{u}=x\vec{i}+y\vec{j}$ et $\vec{v}=x'\vec{i}+y'\vec{j}$
Donc, $\vec{u}\cdot\vec{v}=(x\vec{i}+y\vec{j})\cdot(x'\vec{i}+y'\vec{j})=xx'(\vec{i}\cdot\vec{i})+\underbrace{xy'(\vec{i}\cdot\vec{j})}_{=0}+\underbrace{x'y(\vec{i}\cdot\vec{j})}_{=0}+yy'(\vec{j}\cdot\vec{j})$
D'où, $$\vec{u}\cdot\vec{v}=xx'+yy'$$
Exercice d'application
Le plan est muni d'un repère orthonormé $(O\;;\ \vec{i}\;,\ \vec{j}).$ Soit $A\begin{pmatrix} 1\\ 2\end{pmatrix}\;,\ B\begin{pmatrix} 3\\ 4\end{pmatrix}$ et $C\begin{pmatrix} -2\\ 1\end{pmatrix}$ trois points du plan.
1) Déterminer une équation de la médiatrice de $[AB]$
2) Déterminer une équation du cercle de diamètre $[BC]$
Résolution
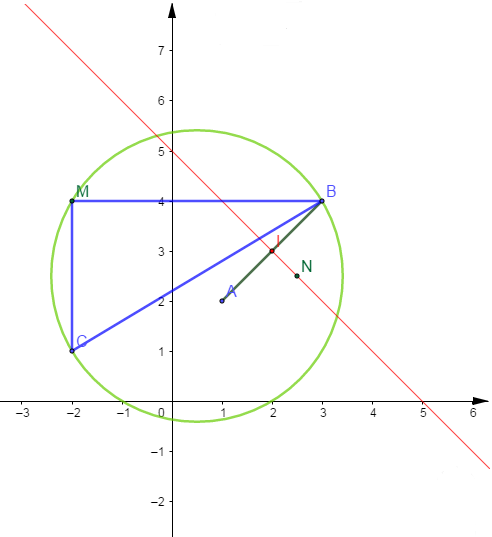
1) Soit $I$ milieu de $[AB]\;;\ I\begin{pmatrix} 2\\ 3\end{pmatrix}.$
$N\begin{pmatrix} x\\ y\end{pmatrix}$ appartenant à la médiatrice de $[AB]$ alors, $\overrightarrow{IN}\begin{pmatrix} x-2\\ y-3\end{pmatrix}\perp\overrightarrow{AB}\begin{pmatrix} 2\\ 2\end{pmatrix}.$
Donc, $\overrightarrow{IN}\cdot\overrightarrow{AB}=0\ \Leftrightarrow\ 2(x-2)+2(y-3)=0$
Ainsi, $(D)\ :\ x+y-5=0$
2) Soit $M\begin{pmatrix} x\\ y\end{pmatrix}\in(\mathcal{C})$ alors, $\overrightarrow{BM}\begin{pmatrix} x-3\\ y-4\end{pmatrix}\perp\overrightarrow{CM}\begin{pmatrix} x+2\\ y-1\end{pmatrix}.$
$$\begin{array}{rcl}\overrightarrow{BM}\perp\overrightarrow{CM}&\Leftrightarrow&\overrightarrow{BM}\perp\overrightarrow{CM}=0\\ \\ &\Leftrightarrow&(x-3)(x+2)+(y-4)(y-1)=0\\ \\ &\Leftrightarrow&x^{2}+y^{2}-x-5y-2=0\end{array}$$
D'où $(\mathcal{C})\ :\ x^{2}+y^{2}-x-5y-2=0$
I.5 Distance d'un point à une droite
Soient $(D)$ la droite d'équation $ax+by+c=0$, $M_{0}\begin{pmatrix}
x_{0}\\
y_{0}
\end{pmatrix}\notin(D)$ un point du plan, $\vec{n}\begin{pmatrix}
a\\
b
\end{pmatrix}$ un vecteur normal à $(D)$. Soit $H\begin{pmatrix}
x_{H}\\
y_{H}
\end{pmatrix}$ le projeté orthogonal de $M_{0}$ sur $(D)$.
x_{0}\\
y_{0}
\end{pmatrix}\notin(D)$ un point du plan, $\vec{n}\begin{pmatrix}
a\\
b
\end{pmatrix}$ un vecteur normal à $(D)$. Soit $H\begin{pmatrix}
x_{H}\\
y_{H}
\end{pmatrix}$ le projeté orthogonal de $M_{0}$ sur $(D)$.
Nous appelons $d(M_{0}, \ (D))$ la distance de $M_{0}$ à $(D)$.
On a : $$d(M_{0}, \ (D))=||\overrightarrow{M_{0}H}||$$
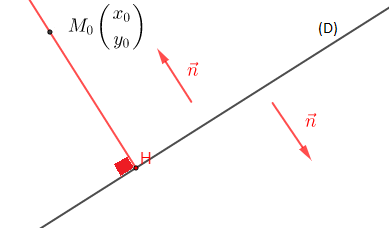
Calculons $\overrightarrow{M_{0}H}\cdot\vec{n}$ de deux façons différentes.
On a :
$$\begin{array}{rcl}\overrightarrow{M_{0}H}\cdot\vec{n} & = & ||\overrightarrow{M_{0}H}||.||\vec{n}||.\cos(\overrightarrow{M_{0}H},\ \vec{n}) \\ \\ & = & a(x_{H}-x_{0})+b(y_{H}-y_{0}) \\ \\ & = & ax_{H}+by_{H}-ax_{0}-by_{0}\end{array}$$
Or, $H\in(D)$ donc, ses coordonnées vérifient l'équation de la droite $(D)$.
$\Rightarrow ax_{H}+by_{H}+c=0$, ce qui donne $ax_{H}+by_{H}=-c$
$\Rightarrow \overrightarrow{M_{0}H}\cdot\vec{n}=-c-ax_{0}-by_{0}$
$\Rightarrow ||\overrightarrow{M_{0}H}\cdot\vec{n}||=|-c-ax_{0}-by_{0}|=|ax_{0}+by_{0}+c|$
On avait $||\overrightarrow{M_{0}H}\cdot\vec{n}||=||\overrightarrow{M_{0}H}||.||\vec{n}||$
donc, $||\overrightarrow{M_{0}H}||=\dfrac{|ax_{0}+by_{0}+c|}{||\vec{n}||}$ $\ $.
Comme $||\vec{n}||=\sqrt{a^{2}+b^{2}}$ alors, $$d(M_{0}, \ (D))=||\overrightarrow{M_{0}H}||=\dfrac{|ax_{0}+by_{0}+c|}{\sqrt{a^{2}+b^{2}}}$$
Exemple
Soit la droite $(D)$ d'équation $2x-y+3=0$ et $A\begin{pmatrix} 5\\ 1\end{pmatrix}$ un point du plan.
Déterminer $d(A\;,\ (D))$
Résolution
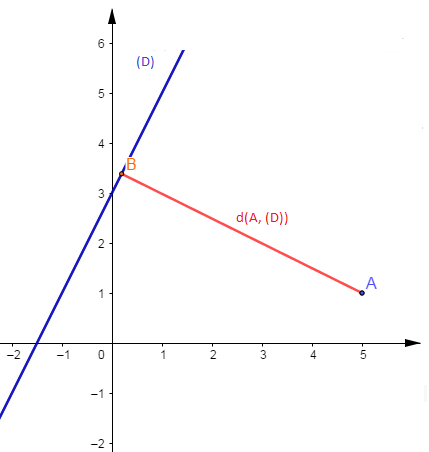
Soit $\vec{n}\begin{pmatrix} 2\\ -1\end{pmatrix}$ un vecteur normal à $(D)$ alors on a : \begin{eqnarray} d(A\;,\ (D))&=&\dfrac{|(2)(5)+(-1)(1)+3|}{\sqrt{2^{2}+(-1)^{2}}}\nonumber \\ \\&=&\dfrac{12}{\sqrt{5}}\nonumber \\ \\&=&\dfrac{12\sqrt{5}}{5}\nonumber \end{eqnarray}
I.6 Relations d'Alkashi
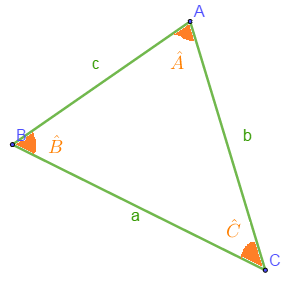
Soit $ABC$ un triangle d'angles $\widehat{A}$, $\ \widehat{B}$ et $\widehat{C}$ respectivement opposés aux cotés $a$, $\ b$ et $c$. Nous avons :
$\centerdot\ \ a^{2}=b^{2}+c^{2}-2bc.cos\widehat{A}$
$\centerdot\ \ b^{2}=a^{2}+c^{2}-2ac.cos\widehat{B}$
$\centerdot\ \ c^{2}=a^{2}+b^{2}-2ab.cos\widehat{C}$
Preuve
On a :
$$\begin{array}{rcl} BC^{2} & = & (\overrightarrow{BA}+\overrightarrow{AC})^{2} \\ \\ & = & (-\overrightarrow{AB}+\overrightarrow{AC})^{2} \\ \\ & = & ||\overrightarrow{AB}||^{2}+||\overrightarrow{AC}||^{2}-2\overrightarrow{AC}\cdot\overrightarrow{AB} \\ \\ & = & ||\overrightarrow{AB}||^{2}+||\overrightarrow{AC}||^{2}-2AB.AC\cos(\overrightarrow{AB},\ \overrightarrow{AC})\end{array}$$
D'où, $\ a^{2}=b^{2}+c^{2}-2bc.cos\widehat{A}$
$$\begin{array}{rcl} AC^{2} & = & (\overrightarrow{AB}+\overrightarrow{BC})^{2} \\ \\ & = & (-\overrightarrow{BA}+\overrightarrow{BC})^{2} \\ \\ & = & ||\overrightarrow{BA}||^{2}+||\overrightarrow{BC}||^{2}-2\overrightarrow{BA}\cdot\overrightarrow{BC} \\ \\ & = & ||\overrightarrow{BA}||^{2}+||\overrightarrow{BC}||^{2}-2BA.BC\cos(\overrightarrow{BA},\ \overrightarrow{BC})\end{array}$$
D'où, $\ b^{2}=c^{2}+a^{2}-2ac.cos\widehat{B}$
$$\begin{array}{rcl} AB^{2} & = & (\overrightarrow{AC}+\overrightarrow{CB})^{2} \\ \\ & = & (-\overrightarrow{CA}+\overrightarrow{CB})^{2} \\ \\ & = & ||\overrightarrow{CA}||^{2}+||\overrightarrow{CB}||^{2}-2\overrightarrow{CA}\cdot\overrightarrow{CB} \\ \\ & = & ||\overrightarrow{CA}||^{2}+||\overrightarrow{CB}||^{2}-2CA.CB\cos(\overrightarrow{CA},\ \overrightarrow{CB})\end{array}$$
$$\begin{array}{rcl} AB^{2} & = & (\overrightarrow{AC}+\overrightarrow{CB})^{2} \\ \\ & = & (-\overrightarrow{CA}+\overrightarrow{CB})^{2} \\ \\ & = & ||\overrightarrow{CA}||^{2}+||\overrightarrow{CB}||^{2}-2\overrightarrow{CA}\cdot\overrightarrow{CB} \\ \\ & = & ||\overrightarrow{CA}||^{2}+||\overrightarrow{CB}||^{2}-2CA.CB\cos(\overrightarrow{CA},\ \overrightarrow{CB})\end{array}$$
D'où, $\ c^{2}=a^{2}+b^{2}-2ab.cos\widehat{C}$
I.7 Relation des sinus
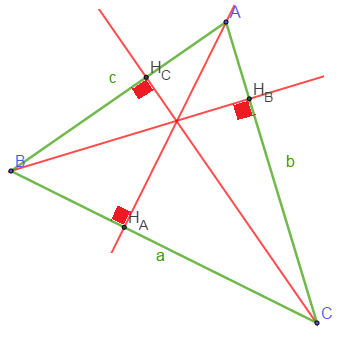
Soit $\mathcal{S}$ l'aire du tringle $ABC$. Considérons $H_{A}$, $\ H_{B}$ et $H_{C}$ les projections orthogonales de $A$, $\ B$ et $C$ sur $(BC)$, $\ (AC)$ et $(AB)$ respectivement. On a : $$\dfrac{sin\widehat{A}}{a}=\dfrac{\sin\widehat{B}}{b}=\dfrac{\sin\widehat{C}}{c}=\dfrac{2\mathcal{S}}{abc}$$
Preuve
On a : $\mathcal{S}=\dfrac{BC\times AH_{A}}{2}=\dfrac{AB\times CH_{C}}{2}=\dfrac{AC\times BH_{B}}{2}$ or,
$\sin\widehat{C}=\dfrac{AH_{A}}{AC} \quad \Rightarrow \ AH_{A}=AC.\sin\widehat{C}=b.\sin\widehat{C}$
$\sin\widehat{B}=\dfrac{CH_{C}}{BC} \quad \Rightarrow \ CH_{C}=BC.\sin\widehat{B}=a.\sin\widehat{B}$
$\sin\widehat{A}=\dfrac{BH_{B}}{AB} \quad \Rightarrow \ BH_{B}=AB.\sin\widehat{A}=c.\sin\widehat{A}$
Donc, $\mathcal{S}=\dfrac{BC.b.\sin\widehat{C}}{2}=\dfrac{AB.a.\sin\widehat{B}}{2}=\dfrac{AC.c.\sin\widehat{A}}{2}$
Ainsi, $\ \mathcal{S}=\dfrac{a.b.\sin\widehat{C}}{2}=\dfrac{c.a.\sin\widehat{B}}{2}=\dfrac{b.c.\sin\widehat{A}}{2}$
Par suite, $\ 2\mathcal{S}=a.b.\sin\widehat{C}=c.a.\sin\widehat{B}=b.c.\sin\widehat{A}$
D'où, $\ \dfrac{2\mathcal{S}}{abc}=\dfrac{sin\widehat{A}}{a}=\dfrac{\sin\widehat{B}}{b}=\dfrac{\sin\widehat{C}}{c}$
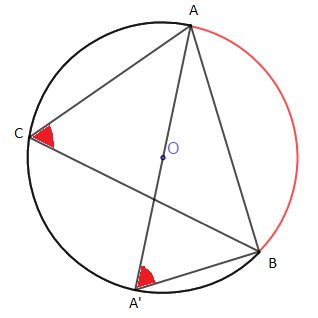
Si de plus nous considérons le cercle $\mathcal{C}$ circonscrit au triangle $ABC$, de centre $O$ (point de rencontre des trois médianes) et de rayon $R.$
Soit $A'$ le symétrique de $A$ par rapport à $O.$ On a :
$\sin\widehat{C}=\sin\widehat{AA'B}=\dfrac{AB}{AA'}\ $ or, $\ AA'=2R\ $ donc, $\ \sin\widehat{C}=\dfrac{c}{2R}$
D'où, $$\dfrac{\sin\widehat{C}}{c}=\dfrac{1}{2R}$$
II. Lignes de niveau
Activité
$A$ et $B$ deux points du plan $\mathcal{P}$ tels $AB=4\;cm.$
On définit l'application $f$ \begin{eqnarray} f\ :\ \mathcal{P}&\rightarrow&\mathbb{R}\nonumber \\ M&\rightarrow&f(M)=\overrightarrow{AB}\cdot\overrightarrow{AM}\nonumber \end{eqnarray}
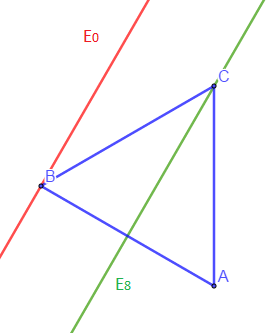
1) Si $C$ est tel que $ABC$ est équilatérale direct, calculer $f(C)$
2) Déterminer l'ensemble $E_{0}$ des points $M$ du plan tels que $f(M)=0$
3) Déterminer l'ensemble $E_{k}$ des points $M$ du plan tels que $f(M)=k$
4) Déterminer l'ensemble $E_{8}$ des points $M$ du plan tels que $f(M)=8$
Résolution
1) Soit $f(M)=\overrightarrow{AB}\cdot\overrightarrow{AM}$
On a : $$\begin{array}{rcl} f(C)&=&\overrightarrow{AB}\cdot\overrightarrow{AC}\\ \\ &=&AB\times AC\times\cos(\overrightarrow{AB}\;,\ \overrightarrow{AC})\\ \\ &=&4\times 4\times\dfrac{1}{2}\\ \\&=&8\end{array}$$
2) $E_{0}=\{M\in\mathcal{P}\;;\ f(M)=0\}$
$\overrightarrow{AB}\cdot\overrightarrow{AM}=0\ \Rightarrow\ \overrightarrow{AB}\perp\overrightarrow{AM}$
$E_{0}$ est donc la perpendiculaire à $(AB)$ passant par $A.$
3) Soit le repère $\left(A\;,\ \dfrac{\overrightarrow{AB}}{4}\right)\;;\ x_{A}=0\;,\ x_{B}=4$

$\overrightarrow{AB}\cdot\overrightarrow{AM}=k\ \Rightarrow\ \overline{AB}\times\overline{AH}_{k}=k$ où $H_{k}$ est le projeté orthogonal de $M$ sur $(AB).$
$$\begin{array}{rcl}\overline{AB}\times\overline{AH}_{k}=k&\Leftrightarrow&(x_{B}-x_{A})(x_{H_{k}}-x_{A})=k\\ \\ &\Leftrightarrow&4x_{H_{k}}=k\\ \\ &\Rightarrow&x_{H_{k}}=\dfrac{k}{4}\end{array}$$
Donc, $E_{k}$ est la perpendiculaire à $(AB)$ passant par $H_{k}$ tel que $x_{H_{k}}=\dfrac{k}{4}$
4) $f(M)=8$ donc $E_{8}$ est la perpendiculaire à $(AB)$ passant par $H_{8}$ tel que $x_{H_{8}}=\dfrac{8}{4}=2.$
Ainsi, $E_{8}$ passe par le milieu de $[AB]$ donc c'est la médiatrice de $[AB].$
Complément
$\centerdot\ \ \mathbf{E}=\left\lbrace M\in\mathcal{P} ;\ \overrightarrow{MA}\cdot\overrightarrow{MB}=0\right\rbrace$ est le cercle de diamètre $[AB]$.
Soit $I$ milieu de $[AB] \ $, on a :
$$\begin{array}{rcl}\overrightarrow{MA}\cdot\overrightarrow{MB}&=&(\overrightarrow{MI}+\overrightarrow{IA})\cdot(\overrightarrow{MI}+\overrightarrow{IB})\\ \\ &=&MI^{2}+\overrightarrow{MI}\cdot\underbrace{(\overrightarrow{IA}+\overrightarrow{IB})}_{=\vec{0}}+\overrightarrow{IA}\cdot\overrightarrow{IB}\\ \\ &=&MI^{2}-\dfrac{\overrightarrow{AB}}{2}\cdot\dfrac{\overrightarrow{AB}}{2}\ =\ 0\\ \\ \Rightarrow\ MI^{2}&=&\dfrac{AB^{2}}{4}\end{array}$$
Et on retrouve bien le cercle de centre $I$ et de rayon $\dfrac{AB}{2}$. C'est tout simplement le cercle de diamètre $[AB]$
$\centerdot\ \ \mathbf{E}=\left\lbrace M\in\mathcal{P} ;\ \overrightarrow{MA}\cdot\overrightarrow{MB}=k>0\right\rbrace$ est le cercle de centre $I$ milieu de $[AB]$ et de rayon $R=\sqrt{k+\dfrac{AB^{2}}{4}}$.
En suivant la même approche du raisonnement précédent on obtient :
$MI^{2}=k+\dfrac{AB^{2}}{4}$
On reconnait bien un cercle de centre $I$; milieu de $[AB]$ et de rayon $R=\sqrt{k+\dfrac{AB^{2}}{4}}$.
Et dans un contexte plus général, il suffit juste d'avoir $k>-\dfrac{AB^{2}}{4}$ pour que le cercle soit bien défini.
$\centerdot\ \ \mathbf{E}=\left\lbrace M\in\mathcal{P} ;\ ||\overrightarrow{MA}||=||\overrightarrow{MB}||\right\rbrace$ est la médiatrice du segment $[AB]$.
Soit $I$ milieu de $[AB]$ , on a :
$$\begin{array}{rcl} ||\overrightarrow{MA}||=||\overrightarrow{MB}|| & \Leftrightarrow & ||\overrightarrow{MA}||^{2}=||\overrightarrow{MB}||^{2} \\ \\ & \Leftrightarrow & ||\overrightarrow{MA}||^{2}-||\overrightarrow{MB}||^{2}=0 \\ \\ & \Leftrightarrow & (\overrightarrow{MA}-\overrightarrow{MB})\cdot(\overrightarrow{MA}+\overrightarrow{MB})=0 \\ \\ & \Leftrightarrow & (\overrightarrow{MI}+\overrightarrow{IA}-\overrightarrow{MI}-\overrightarrow{IB})\cdot(\overrightarrow{MI}+\overrightarrow{IA}+\overrightarrow{MI}+\overrightarrow{IB})=0 \\ \\ & \Leftrightarrow & 2\overrightarrow{BA}\cdot\overrightarrow{MI}=0 \\ \\ & \Leftrightarrow & \overrightarrow{AB}\cdot\overrightarrow{MI}=0\end{array}$$
On reconnait la perpendiculaire à $(AB)$ passant par $I$. C'est la médiatrice du segment $[AB]$.
Théorème de la médiane
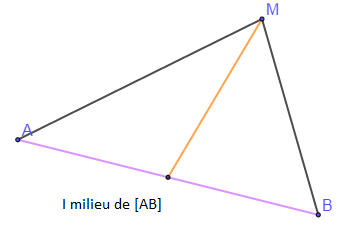
Soient $I$ milieu du segment $[AB]$ et $M$ un point du plan tel que $MBA$ soit un triangle. Alors on a :
$\overrightarrow{MI}=\dfrac{1}{2}(\overrightarrow{MA}+\overrightarrow{MB})$
$$MA^{2}+MB^{2}=2MI^{2}+\dfrac{AB^{2}}{2}$$
Preuve
$I$ milieu de $[AB]$, alors $I$ est isobarycentre de $A$ et $B$, donc on a :
$\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI} \ \Rightarrow \ \overrightarrow{MI}=\dfrac{1}{2}(\overrightarrow{MA}+\overrightarrow{MB})$
$$\begin{array}{rcl} MA^{2}+MB^{2} & = & (\overrightarrow{MI}+\overrightarrow{IA})^{2}+(\overrightarrow{MI}+\overrightarrow{IB})^{2} \\ \\ & = & MI^{2}+IA^{2}+2\overrightarrow{MI}\cdot\overrightarrow{IA}+MI^{2}+IB^{2}+2\overrightarrow{MI}\cdot\overrightarrow{IB} \\ \\ & = & 2MI^{2}+IA^{2}+IB^{2}+2\overrightarrow{MI}\cdot(\overrightarrow{IA}+\overrightarrow{IB})\end{array}$$
Or, $IA=IB=\dfrac{AB}{2}$ et $\overrightarrow{IA}+\overrightarrow{IB}=\vec{0}$
D'où, $MA^{2}+MB^{2}=2MI^{2}+\dfrac{AB^{2}}{4}+\dfrac{AB^{2}}{4}=2MI^{2}+\dfrac{AB^{2}}{2}$
Travaux Pratiques
Soit $A$ et $B$ deux points du plan tels que $AB=6.$
Déterminons l'ensemble des points $M$ du plan tels que $2MA^{2}+3MB^{2}=k$
Soit $G$ barycentre de $(A\;,\ 2)\;,\ (B\;,\ 3)$
On a :
$$\begin{array}{rcl} 2MA^{2}+3MB^{2}=k&\Leftrightarrow&2(\overrightarrow{MG}+\overrightarrow{GA})^{2}+3(\overrightarrow{MG}+\overrightarrow{GB})^{2}=k \\ \\ &\Leftrightarrow&2(MG^{2}+2\overrightarrow{MG}\cdot\overrightarrow{GA}+GA^{2})+3(MG^{2}+2\overrightarrow{MG}\cdot\overrightarrow{GB}+GB^{2})=k \\ \\ &\Leftrightarrow&5MG^{2}+4\overrightarrow{MG}\cdot\overrightarrow{GA}+6\overrightarrow{MG}\cdot\overrightarrow{GB}+2GA^{2}+3GB^{2}=k \\ \\ &\Leftrightarrow &5MG^{2}+2\overrightarrow{MG}\cdot\underbrace{(2\overrightarrow{GA}+3\overrightarrow{GB})}_{=\vec{0}}+2GA^{2}+3GB^{2}=k \\ \\ &\Leftrightarrow & MG^{2}=\dfrac{k-2GA^{2}-3GB^{2}}{5}\end{array}$$
$-\ $ si $\;\dfrac{k-2GA^{2}-3GB^{2}}{5}<0\;,\ \mathbf{E}_{k}=\emptyset$
$-\ $ si $\;\dfrac{k-2GA^{2}-3GB^{2}}{5}=0\;,\ \mathbf{E}_{k}=\{G\}$
$-\ $ si $\;\dfrac{k-2GA^{2}-3GB^{2}}{5}>0\;$ alors $\;MG=\sqrt{\dfrac{k-2GA^{2}-3GB^{2}}{5}}$
D'où, $\mathbf{E}_{k}$ est le cercle de centre $G$ et de rayon $r=\sqrt{\dfrac{k-2GA^{2}-3GB^{2}}{5}}$
$$\mathbf{E}_{k}=\mathcal{C}\left(G\;,\ \sqrt{\dfrac{k-2GA^{2}-3GB^{2}}{5}}\right)$$
Auteur:
Diny Faye & Seyni Ndiaye

Ajouter un commentaire