Calcul vectoriel 2nd : Savoir-faire
Classe:
Seconde
Rappels de cours
I. Rappels sur les vecteurs
a) Un vecteur non nul est caractérisé par sa direction, son sens et sa norme.
Le vecteur nul n'a pas de direction.
Deux vecteurs $\overrightarrow{AB}$ et $\overrightarrow{CD}$ sont égaux si et seulement si ils ont même direction, même sens et même norme.
Cela signifie que le quadrilatère $ABDC$ est un parallélogramme (éventuellement aplati).
Étant donné un point $O$ et un vecteur, il existe un unique point $M$ tel que $\overrightarrow{OM} =\vec{u}$ (Axiome d'Euclide)
b) Les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{BA}$ sont opposés. On note :
$$\overrightarrow{BA} = -\overrightarrow{AB}$$
$$\overrightarrow{BA} = -\overrightarrow{AB}$$
c) Soient $A\;,\ B$ et $C$ 3 points quelconques, éventuellement égaux. On a la relation de Chasles : $$\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$$
On définit ainsi la somme de 2 vecteurs $\vec{u}=\overrightarrow{AB}$ et $\vec{v}=\overrightarrow{BC}$
d) $\overrightarrow{AB}=\vec{0}$ équivaut à $A \ = \ B$
e) Pour dessiner $\vec{u} +\vec{v}$, on dessine un représentant de $\vec{u}$ et un représentant $\vec{v}$ de la même origine. $\vec{u} +\vec{v}$est alors l'une des diagonales du parallélogramme construit sur $\vec{u}$ et $\vec{v}$..
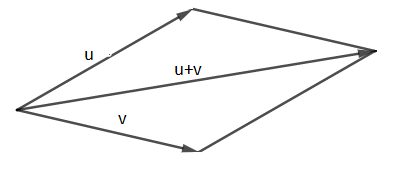
Autre méthode : dessiner à l'extrémité du vecteur $\vec{u}$ un représentant du vecteur $\vec{v}$(Utilisation de la relation de Chasles).
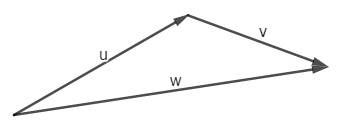
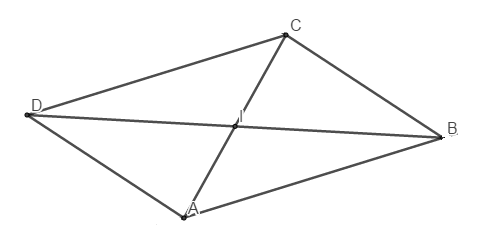
f) Le quadrilatère $ABCD$ est un parallélogramme si et seulement si on a l'une des conditions suivantes :
$^*)$ $\overrightarrow{AB}=\overrightarrow{DC}$ $^*)$ $\overrightarrow{AD}=\overrightarrow{BC}$ $^*)$ $\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$
$^*)$ Les diagonales $[AC]$ et $[BD]$ ont même milieu.
g) Pour tous vecteurs $\vec{u}$, $\vec{v}$ et $\vec{w}$, on a :
$^*)$ $\vec{u}+\vec{v}=\vec{v}+\vec{u}$ $^*)$ $\vec{u}+ (\vec{v}+\vec{w}) \ = ( \vec{u}+ \vec{v})+\vec{w}$ $^*)$ $\vec{u}+\vec{0}=0+\vec{u} =\vec{u}$.
h) Le produit du réel $\alpha$ (non nul) par le vecteur $\vec{u}$ est le vecteur noté $\alpha .\vec{u}$ et ayant :
$-\ \ $ la même direction direction que $\vec{u}$
$-\ \ $ le sens du $\vec{u}$ si $\alpha>0$ et les sens contraires de $\vec{u}$ si $\alpha >0$
$-\ \ $ pour norme $ |\alpha|\times ||\vec{u}||$.
i) Pour tout réel $\alpha$ et tous vecteurs $\vec{u}$ et $\vec{v}$, on a :
$^*)$ $\alpha (\vec{u}+\vec{v})=\alpha \vec{u}+\vec{v}$ $^*)$ $\alpha (\beta \vec{u})=(\alpha \beta)\vec{u}$ $^*)$ $1(\vec{u}=\vec{u}$
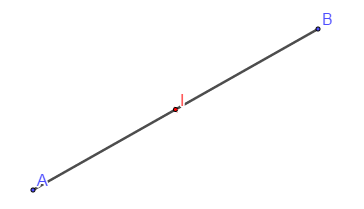
j) $I$ est le milieu du segment $[AB]$ se traduit par l'une des conditions suivantes :
$^*) \ \overrightarrow{AI}=\frac{1}{2}\overrightarrow{AB}$ $^*) \ \overrightarrow{IA}+\overrightarrow{IB}=\vec{0}$ $^*) \ \overrightarrow{AI}=\overrightarrow{IB}$
Pour tout point $M$ du plan, on a :$\ \overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}$
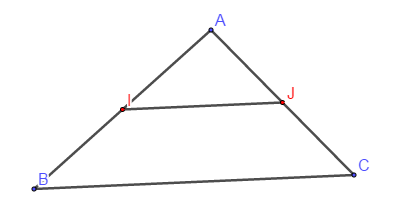
k) Soit $ABC$ un triangle, $I$ milieu de $[AB]\;,\ J$ milieu de $[AC].$ On a : $\ \overrightarrow{IJ}=\dfrac{1}{2}\overrightarrow{BC}$
l) Deux vecteurs $\vec{u}$ et $\vec{v}$ sont dits colinéaires si l'un d'eux est nul ou bien s'ils ont la même direction. Cela équivaut à l'existence d'un réel $\alpha$ tel que $\vec{u}=\alpha \vec{v}$, ou $\vec{v}=\alpha \vec{u}$.
m) Les points $A\;,\ B$ et $C$ sont alignés si et seulement si les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$ sont colinéaires, c'est-à-dire qu'il existe un réel $\alpha$ tel que $\overrightarrow{AB}=\alpha \overrightarrow{AC}$ ou $\overrightarrow{AC}=\alpha \overrightarrow{AB}$.
n) Les droites $(AB)$ et $(CD)$ sont parallèles si et seulement si les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$ sont colinéaires.
Remarque
Pour prouver que les vecteurs $\overrightarrow{IJ}$ et $\overrightarrow{IK}$ sont colinéaires, on peut les exprimer en fonction de deux vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$ dont on sait qu'ils sont non colinéaires, puis comparer ces deux expressions pour en déduire une relation entre $\overrightarrow{AB}$ et $\overrightarrow{CD}$.
II. Approche basée sur les compétences exigibles
II.1 Construire une combinaison linéaire de vecteurs
II.1.1 Représenter une somme ou une différence de vecteurs
Méthode
Pour représenter la somme de deux vecteurs,
$\centerdot\ \ $ Lorsque les deux vecteurs sont "bout à bout", on peut appliquer directement la relation de Chasles :
$$\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$$
$$\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$$
$\centerdot\ \ $ Sinon, quitte à remplacer l'un des vecteurs par un vecteur qui lui est égal, on peut se ramener à la situation où les vecteurs ont même origine. On construit alors un parallélogramme.
Pour soustraire deux vecteurs, on fait la somme du premier et de l'opposé du deuxième.
II.1.2 Représenter un point défini par une relation de colinéarité
Méthode
Soit $ABC$ un triangle.
$\centerdot\ \ $ Pour représenter un point $E$ défini par une relation vectorielle du type $$\overrightarrow{AE}=k\overrightarrow{AB}$$
Il faut d'abord remarquer que cette relation entraîne que $E$ est un point de la droite $(AB).$ Le signe permet de choisir une des deux demi-droites d'origine $A.$
$\centerdot\ \ $ Pour représenter un point $F$ défini par une relation vectorielle du type $$\overrightarrow{BF}=k\overrightarrow{AC}$$
Il faut remarquer que cette relation exprime le fait que $F$ est situé sur la droite parallèle à $(AC)$ passant par $B.$
II.1.3 Représenter une combinaison linéaire de deux vecteurs
Méthode
Utiliser simultanément les deux méthodes précédentes.
II.2 Décomposer un vecteur à l'aide de la relation de Chasles
Méthode
On peut décomposer, à l'aide de la relation de Chasles, un vecteur quelconque en la somme de deux ou plusieurs autres. La condition à respecter est que, dans cette nouvelle écriture, le premier vecteur écrit doit avoir même origine que le vecteur de départ et le dernier vecteur doit avoir même extrémité que lui. D'autre part, entre deux vecteurs "voisins", il doit toujours y avoir la même lettre à l'extrémité du premier qu'au début du second.
Dans le cas d'une relation de colinéarité, il faut décomposer les vecteurs en utilisant des points bien choisis.
II.3 Passer de la relation vectorielle $\overrightarrow{AC}=\lambda\overrightarrow{AB}$ à la relation algébrique $AC=|\lambda|AB$
Méthode
Il faut tout d'abord trouver le coefficient de colinéarité entre deux vecteurs, puis passer aux normes
II.4 Utiliser les relations vectorielles pour démontrer des propriétés géométriques (distance, alignement, milieu, parallélisme)
Auteur:
Mouhamadou Ka
Professeur au Lycée Lamine Guèye

Commentaires
Anonyme (non vérifié)
ven, 09/18/2020 - 11:03
Permalien
svp aidez moi tout de suite
Anonyme (non vérifié)
dim, 01/17/2021 - 10:50
Permalien
Aïcha
Anonyme (non vérifié)
mer, 01/20/2021 - 21:53
Permalien
Prk on peut pas tlchgé ce
Amadou kane (non vérifié)
dim, 10/24/2021 - 12:44
Permalien
Apprentissage
Amadou kane (non vérifié)
dim, 10/24/2021 - 12:45
Permalien
Cours et exercices
mayé faye (non vérifié)
ven, 10/13/2023 - 21:19
Permalien
aidez moi svp je ne peux pas
Ajouter un commentaire