Bac Maths, S Polynésie mars 2023

Épreuve d'enseignement de spécialité

Les parties $A$ et $B$ peuvent être traitées indépendamment

Chaque jour, un athlète doit sauter une haie en fin d'entraînement. 

 

Son entraîneur estime, au vu de la saison précédente que

 

$\bullet\ $si l'athlète franchit la haie un jour, alors il la franchira dans $90\%$ des cas le jour suivant ; 

 

$\bullet\ $si l'athlète ne franchit pas la haie un jour, alors dans $70\%$ des cas il ne la franchira pas non plus le lendemain.

 

On note pour tout entier naturel $n$ :

 

$\bullet\ $ $\mathbb{R_{n}}$ l'évènement : « L'athlète réussit à franchir la haie lors de la $n$-ième séance »,

 

$\bullet\ $ $p_{n}$ la probabilité de l'évènement $\mathbb{R_{n}}$ 

 

On considère que $p_{o}=0.6$

 

1. Soit n un entier naturel, recopier l'arbre pondéré ci-dessous et compléter les pointillés.

 

 

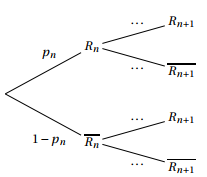
2. Justifier en vous aidant de l'arbre que, pour tout entier naturel $n$, on a 

$$p_{n+1}=0.6p_n+0.3$$

 

3. On considère la suite $\left(u_{n}\right)$ définie, pour tout entier naturel $n$, par 

 

a. Démontrer que la suite $\left(u_{n}\right)$ est une suite géométrique dont on précisera la raison et le premier terme.

 

b. Démontrer que, pour tout entier $n$ naturel $n$ :

$$p_n=0.75-0.15\times {0.6}^n$$

 

En déduire que la suite $\left(p_{n}\right)$ est convergente et déterminer sa limite $ell$

 

d. Interpréter la valeur de ℓ dans le cadre de l'exercice.

Après de nombreuses séances d'entraînement, l'entraineur estime maintenant que l'athlète franchit chaque haie avec une probabilité de $0.75$ et ce indépendamment d'avoir franchi ou non les haies précédentes.

 

On note $X$ la variable aléatoire qui donne le nombre de haies franchies par l'athlète à l'issue d'un $400$ mètres haies qui comporte $10$ haies,

 

1. Préciser la nature et les paramètres de la loi de probabilité suivie par $X.$

 

2. Déterminer, à $10^{-3}$ près, la probabilité que l'athlète franchisse les $10$ haies.

 

3. Calculer $p\left(X\geq 9\right)$ près

L'espace est muni d'un repère orthonormé $\left(O\ ; \vec{i}\;,\vec{j}\;,\vec{k}\right)$

 

On considère :

 

$\bullet\ $Le point $A(1\ ;\ -1\ ;\ -1)$ ;

 

$\bullet\ $Le plan $\mathfrak{p}_{1}$, d'équation : $5x+2y+4z=14$ ; 

 

$\bullet\ $Le plan $\mathfrak{p}_{2}$ d'équation : $10x+14y+3z=19$ ; 

 

$\bullet\ $La droite $\mathfrak{D}$ de représentation paramétrique :

 

$\left\lbrace\begin{array }{rcl} x&=&1+2t\ y&=&-t\quad\text{où }t\text{ décrit }\mathbb{R}\ z&=&3-2t \end{array}\right.$

 

1. Justifier que les plans $\mathfrak{P}_{1}$ et $\mathfrak{P}_{2}$ ne sont pas parallèles.

 

2. Démontrer que $\mathfrak{D}$ est la droite d'intersection de $\mathfrak{P}_{1}$ et $\mathfrak{P}_{2}.$

 

3. a. Vérifier que $A$ n'appartient pas à $\mathfrak{P}_{1}$

 

b. Justifier que $A$ n'appartient pas à $\mathfrak{D}.$

 

Pour tout réel $t$, on note $M$ le point de $\mathfrak{D}$ de coordonnées $(1+2t ; -t ; 3-2t)$

 

On considère alors la fonction $f$ qui à tout réel $t$ associe $AM^{2}$, soit $f(t)=AM^{2}.$

 

a. Démontrer que pour tout réel $t$, on a : 

 

$f(t)=9t^{2}-18t+17$

 

b. Démontrer que la distance $AM$ est minimale lorsque $M$ a pour coordonnées $(3 ; -1 ; 1)$

 

5. On note $H$ le point de coordonnées $(3 ; -1 ; 1)$

 

Démontrer que la droite $(AH)$ est perpendiculaire à $\mathfrak{D}$

Les parties $A$ et $B$ peuvent être traitées indépendamment

Le plan est ramené à un repère orthogonal.

 

On a représenté ci-dessous la courbe d'une fonction $f$ définie et deux fois dérivable sur $\mathfrak{R}$, ainsi que celle de sa dérivée $f'$ et de sa dérivée seconde $f"$

 

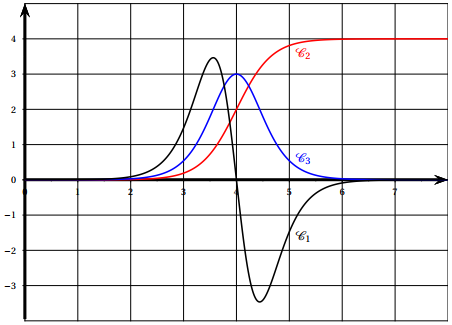
1. Déterminer, en justifiant votre choix, quelle courbe correspond à quelle fonction.

 

2. Déterminer, avec la précision permise par le graphique, le coefficient directeur de la tangente à la courbe $\mathfrak{C_{1}}$ au point d'abscisse $4.$

 

3. Donner avec la précision permise par le graphique, l'abscisse de chaque point d'inflexion de la courbe $\mathfrak{C_{1}}$

Soit un réel k strictement positif.

 

On considère la fonction $g$ définie sur $\mathcal{R}$ par :

$$g(x)={\displaystyle \frac{4}{1+e^{-k{x}^{\cdot }}}}$$

 

1. Déterminer les limites de $g$ en $+\infty$ et en $-\infty$,

 

2. Prouver que $g'(0)=k.$

 

3. En admettant le résultat ci-dessous obtenu avec un logiciel de calcul formel, prouver que la courbe de $g$ admet un point d'inflexion au point d'abscisse $0.$

 

$$$\text{Extra close brace or missing open brace}$$$

Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse. 

 

Chaque réponse doit être justifiée. 

 

Une réponse non justifiée ne rapporte aucun point :

 

1. Affirmation : La suite $u$ définie pour tout entier naturel $n$ par $u_{n}=\dfrac{(-1)^{n}}{n+1}$ est bornée.

 

2. Affirmation : Toute suite bornée est convergente.

 

3. Affirmation : Toute suite croissante tend vers $+\infty$

 

4. Soit la fonction $f$ définie sur $\mathcal{R}$ par $f(x)=\ln\left(x^{2}+2x+2\right)$

 

Affirmation : La fonction $f$ est convexe sur l'intervalle $[-3\ ;\ 1]$

 

On considère la fonction mystère définie ci-dessous qui prend une liste $L$ de nombres en paramètre.

 

On rappelle que $1$ en $(L)$ renvoie la longueur, c'est-à-dire le nombre d'éléments de la liste $L.$

 

$\bosed{\text{def mystère}(L) : \ M=L[0]\ #\text{On initialise }M{avec le premier élément de la liste }L\ \text{for }i\text{in range (1\text{en}}(L)) : \ if L[i]> M : \ M=L[i]\ \text{return }M}$

 

Affirmation : L'exécution de mystère $([2,3, 7, 0, 6, 3, 2, 0, 5])$ renvoie $7.$