1. Fonction logarithme.

    1.1.  Définition et propriétés

Définition : La fonction logarithme népérien est une fonction, notée $ln~ x$ , qui vérifie les propriétés suivantes : elle est définie sur $]0 ; +\infty[$ ;$ ln~1 = 0$ et dérivable sur $]0 ; +\infty [$ et sa dérivée est la fonction inverse, autrement dit $(ln x)’ = \frac{1}{x}$ .

Conséquences

• $ln~ 0$ ou $ln(–3)$ n'ont pas de sens...
• La fonction $ln$ étant dérivable sur $]0 ; +\infty[$, elle est continue sur cet intervalle.
• La fonction $ln$ a pour dérivée $\frac{1}{x}$ : on dit aussi que $\frac{1}{x}$ a pour primitive $ln~ x$ sur l’intervalle $]0 ; +\infty[$.
• Comment calculer $ln~ x$ ?: Il n'y a pas si longtemps, on utilisait des tables numériques....Aujourd'hui, on dispose de la touche ln de nos calculatrices, qui ne donne, dans la plupart des cas, qu'une valeur approchée de $ln~ x$.

    1.2.  Les propriétés algébriques de la fonction ln x

         a. Propriété fondamentale

Soient les réels strictements positifs , on a :

                    $ln~ ab = ln~ a + ln~ b$

On dit que la fonction logarithme transforme les produits en sommes.

         b. Conséquence : les autres propriétés algébriques

Pour tous réels strictement positifs a et b, et tout entier relatif n, on a :

• $ln~ a^ n = n ln~ a$
• $ln \frac{a}{b} = ln~ a – ln~ b$  en particulier        $ln \frac{1}{b} = ln~ a – ln~ b$             .
• $ln\sqrt{a} =\frac{1}{2} ln~ a$

Applications : Calculer sans calculatrice                     

$ln(e^2) ;  ln(\frac{1}{e}) ;  ln(\frac{1}{e^3}) ;  ln(\sqrt{e})$

Solution :

$ln(e^2)= 2$   $ln(\frac{1}{e})=-1$   $ln(\frac{1}{e^3})=-3$   $ln(\sqrt{e})=\frac{1}{2}$

         c. Résolution de l’équation   a^x = b

Pour tout $a > 0$  et $a \neq 1$ , et pour tout $b > 0$.

Pour résoudre l’équation $a^x = b$ d’inconnue $x$, on utilise une des propriétés du logarithme népérien :

$ln(a^x) = ln~b$   équivaut à    $x ln~a = ln~b$,    d’où : $x = \frac{ln~b}{ln~a}$

Applications :

• Résoudre l’équation                 2^x = 1024                   x = 10
• La population d’une ville s’accroît chaque année de 1%. Dans combien d’année la population sera-t-elle passée de 45 000 à 49 216 habitants ?

Équivaut à résoudre 49216 = 45000 x 1,01ⁿ ,  soit  ln 49 216 = ln(45000 x 1,01ⁿ)

D’où               $n = \frac{ln~ 49 216 – ln~ 45 000}{ln~ 1,01} = 9 ans$

      1.3.  Étude de la fonction logarithme népérien

         a. Définition  de la fonction ln x

La fonction $ln ~ x$  est définie sur $]0 ; +\infty[$. Comme elle est dérivable sur cet intervalle, elle est aussi continue sur $]0 ; +\infty[$. $(ln x)’\frac{1}{x} = > 0$pour x > 0 : par suite la fonction $ln$ est strictement croissante.

• Tous les résultats sont résumés par le tableau de variation suivant.

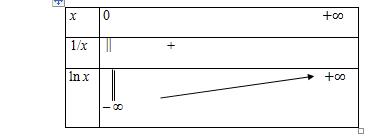
On obtient la représentation graphique suivante :

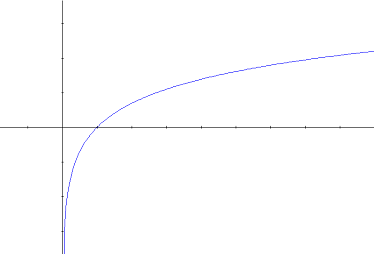
Le signe de ln x se déduit du sens de variation de f :  

ln x < 0 équivaut à 0 < x < 1

ln x = 0 équivaut à x = 1               

ln x > 0 équivaut à x > 1.

• ln A = ln B équivaut à A = B    et        
• ln A < ln B équivaut à A < B

b. Le nombre e : Comme ln 2 < 1 et ln 3 > 1, l’équation ln x = 1 admet une seule solution sur l’intervalle [2 ; 3]: il existe un seul nombre réel noté e tel que ln e =1 Le nombre e est appelé base des logarithmes népériens. Une valeur approchée de e avec 3 décimales exactes est :

e 2,718

On peut remarquer que pour tout entier relatif n, on a :

ln (eⁿ) = n.

      1.2. Fonction logarithme décimal

         a.  Définition

Pour tout x,   log (10^x)  = x.  Où alors,   y = logx  alors  x = 10^y

         b. Sens de variation et tracé de la courbe y = logx

Remplir à l’aide de la touche "log" de la calculatrice le tableau de valeurs suivant, arrondir les valeurs au dixième.

Puis tracer la courbe y = log x sur l'intervalle [0,01 ; 10]

On admettra le tableau de variation suivant,

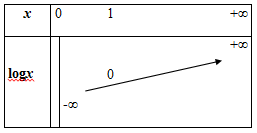
         c. Propriétés

Soient   a et  b deux nombres strictement positifs

•    $ log~ab = log~  a + log~ b$
•    $ log\frac{a}{b}  = log~ a – log~ b$
•    $ log~ a^n   = nlog~ a$
•     $log~ 10 = 1$

Applications :
a. Calculer sans calculatrice les valeurs de $ log~10^3$, $log~10^{-5}$, $log \sqrt[3]{10}$
$ log~10^3 = 3 \times log~10 = 3 \times 1 = 3$ ;$ log~10^{-5} = -5$ ; $log \sqrt[3]{10}=\frac{3}{2} \times log~ 10=1,5\times1 =1,5$
b. On pose $a = log~2$ et $b = log~3$ : Exprimer en fonction de a et b les nombres suivants :    $log~4$ ; $log~5$ ; $log~6$ ; $log~8$ ; $log~9$ ; $log~12$ ; $log~15$ ; $log~16$ ; $log~18$ ; $log~20$.

$log~4 = 2a$    $log~5 =$ pas de sol.    $log~6 = a + b$    $log~8 = 3a$    $log~9 = 3b$    $log~12 = b + 2a$
$log15 = b + log~5$    $log~16 = 4a$    $log~18 = a + 3b$    $log~20 = 2a + log~5$
    
c. Un capital de 100 000€ (notée $C_0$) : est placé à intérêts composés au taux de 3%.
a. Exprimer le capital $C_n$ de la nième année en fonction de $C_0$.
$C_n = C_0\times (1,03)^n$
b. Calculer la valeur acquise au bout de 7ans, 11 ans et 15 ans.
$C_7 = 122 987$€        $C_11 = 138 423$€        $C_15 = 155 797$€
c. Au bout de combien d'années ce capital aura-t-il doublé ?
$100 000 \times (1,03)^n = 200 000$    soit     $(1,03)^n = 2$    $n = \frac{log2}{log1,03}= 23,5$ ans

2.  Fonction exponentielle.

      2.1. Fonctions exponentielles

 Définition : Soit a >0. La fonction $f : x \mapsto a^x$ est appelée fonction exponentielle de base a.
 Exemples :Les fonctions $f(x) = 2^x$ ; $g(x) = 0,5^x$ ; $h(x) = e^x$ sont des fonctions exponentielles de bases respectives 2 ; 0,5 ; e.
Sur la calculatrice on utilise les touches  $〖  x〗^y$      et $〖  e〗^x$      pour déterminer leurs valeurs.
Propriétés : Soit a un réel strictement positif ( différent de 1), On admettra que pour tous réels x et y :
$ax > 0$                 $a^x =\frac{1}{a^x}$            $a^x \times a^y = a^{x+y}$
$\frac{a^x}{a^y}= a^{x-y}$            $(a^x)^y = a^{xy}$            $a^x \times b^x = (ab)^x$
Remarque : Pour tout x réel, la fonction exponentielle de base a définie par
$x \mapsto ax (a >0$  et  $a \neq 1$) peut également être définie de la manière suivante :
$x \mapsto e^{x lna}$

      2.2. Fonction exponentielle de base e :

La  fonction exponentielle de base e est la fonction définie par $x \mapsto e^x$

A l’aide de la calculatrice, remplissons le tableau de valeurs suivant,

Tracer la fonction sur cet intervalle.

 On admet le tableau de variation de la fonction

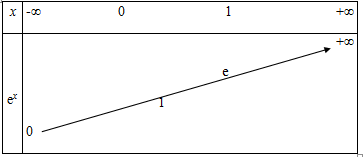
Applications
1. Écrire plus simplement,
$e^{ln~3} = 3^1 = 3$              $e^{-ln2} = 2^{-1} = \frac{1}{2}$            $e^{\frac{1}{2}ln~5} = 5^{0,5}$
2. Résoudre les équations suivantes,
a) $e^{x+1} = 1$         b) $e^2x = 1$         c) $e^x = 2$
d) $e^2x = 2$ soit $x = \frac{ln2}{2} = 0,35$           e) $2^x = 5$ soit $x= \frac{ln5}{ln2} = 2,3$
 f) $(1,05)^x = 3$ soit $x = \frac{ln~3}{ln~1,05} = 22,5$   g) $(1,07)^x = 6000$ soit $x = \frac{ln~6000}{ln~1,07} = 128,6$

Exercices d’application
Résoudre dans R les équations suivantes :

• $e^{x+1} = 1$  ;      $e^{2x} = 1$   ;      $e^x = 2$     ;      $(1,05)^x  =3$   ;       $(1,07)^x =6000$
• $ln ( 3x – 2 ) = 0$        ;    $ln ( 3x – 2 ) + ln ( 2x + 4 ) = ln ( x + 2 )$
• $ln ( x – 4 ) + ln ( x – 1 ) = 1$     ;    $2.(ln ( x ))^2 – 3.ln ( x ) – 5 = 0$
• $(ln ( x ))^2 – ln ( x^2 ) – 3 = 0$    ;    $2.(ln ( x ))^2 – 7.ln ( x ) + 6 = 0$