Bac Maths D, Tunisie 2012

Pour chacune des questions suivantes, une seule des trois réponses proposées est exacte.

Le candidat indiquera sur sa copie le numéro de la question et la lettre correspondant à la réponse choisie.

Aucune justification n'est demandée.

L'espace est rapporté à un repère orthonormé direct $(O\;,\ \vec{i}\;,\ \vec{j}\;,\ \vec{k}).$

On considère les points $A(1\;,\ 0\;,\ 0)$, $B(0\;,\ 1\;,\ 0)$ et $C(0\;,\ 0\;,\ 2).$

1. Le vecteur $\overrightarrow{OB}\wedge\overrightarrow{OC}$ es égale à

a. $\overrightarrow{OA}$           

b. $2\overrightarrow{OA}$                 

c. $−2\overrightarrow{OA}$

2. Le réel $\dfrac{1}{6}\left(\overrightarrow{AB}\wedge\overrightarrow{AO}\right)\cdot\overrightarrow{AC}$ est égal à  

a. $0$      

b.$\dfrac{1}{3}$      

c. $2.$

3. La droite $(BC)$ est l'intersection des plans d'équations

a. $x=1$ et $2y+z-2=0.$

b. $x=0$ et $y+2z-1=0.$

c. $x=0$ et $2y+z-2=0.$

4. Une équation de la sphère de centre $O$ et tangente au plan $(ABC)$ est  

a. $x^{2}+y^{2}+z^{2}=1.$

b. $x^{2}+y^{2}+z^{2}=\dfrac{4}{9}.$

c. $x^{2}+y^{2}+z^{2}-2x=\dfrac{4}{9}$

Le plan est muni d'un repère orthonormé direct $(O\;,\ \vec{u}\;,\ \vec{v}).$
 
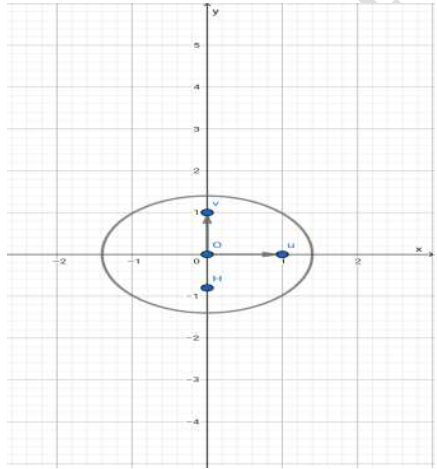
On désigne par $(\mathcal{C})$ le cercle de centre $O$ et de rayon $1$ et par $I$ et $A$ les points d'affixes respectives $1$ et $a=\sqrt{3}+\mathrm{i}.$
 
1. a) Donner la forme exponentielle de $a.$
 
b) Construire $A.$
 
2. Soit $B$ le point d'affixe $b=\dfrac{a−1}{1−a}.$
 
a. Vérifier que $b\bar{b}=1.$
 
En déduire que le point $B$ appartient au cerclé $(\mathcal{C}).$

b. Montrer que $\dfrac{b-1}{a-1}$ est un réel.

En déduire que les points $A$, $B$ et $I$ sont alignés.

c. Construire le point $B$ dans le repère.

3. Soit $\theta$ un argument du nombre complexe $b.$

Montrer que $\cos\theta=\dfrac{2\sqrt{3}-3}{5-2\sqrt{3}}$ et $\sin\theta=\dfrac{2-2\sqrt{3}}{5-2\sqrt{3}}.$

$$\begin{array}{|l|c|c|c|c|} \hline \text{Groupe}&A&B&AB&O\\ \hline  \text{Pourcentage}&31\%&18\%&5\%&46\%\\  \hline \end{array}$$

Le centre National de la Transfusion sanguine a diffusé le tableau ci-contre donnant la répartition des groupes sanguins en Tunisie.

I. 1. Quelle est la probabilité qu'un tunisien ait un sang du groupe $O$ ?     

2. Quatre donneurs se présentent dans un centre de transfusion sanguine.         

a. Quelle est la probabilité qu'un seul parmi les quatre ait un sang du groupe $O$ ?          

b. Quelles est la probabilité de trouver les quatre groupes sanguins chez ces donneurs ?
 
II. In dépendamment du groupe sanguin, le sang peut posséder le facteur Rhésus.

Si le sang d'un individu possède ce facteur, il est dit Rhésus positif $\left(Rh_{+}\right)$, sinon il est dit de Rhésus négatif $\left(Rh^{-}\right).$

Un individu ayant un sang de groupe $O$ et de Rhésus négatif est appelé un donneur universel.

En Tunisie, $9\%$ des individus du groupe $O$ sont de Rhésus négatif.

1. Montrer que la probabilité qu'un tunisien soit un donneur universel est $0.0414.$

2. Dans un centre de transfusion sanguine, $n$ donneur se représentent.

On note $X$ la variable aléatoire égale au nombre de donneur universels parmi les $n$ donneurs.

a. Déterminer la loi de probabilité de $X.$

b. Déterminer l'espérance de $X$ en fonction de $n.$

c. Déterminer le nombre moyen des donneurs universels parmi $5000$ donneurs.

A l'instant $t=0(t$ exprimé en heures$)$ un médecin injecte à un patient une dose de $1.4\,mg$ d'une substance médicamenteuse qui n'est pas présente dans le sang.

Cette substance se répartit instantanément dans le sang, ensuite elle est progressivement éliminée.

On note $Q(t)$ la quantité de substance $($en $mg)$ présente dans le sang à l'instant $t$, $(t\geq 0).$

On admet que la fonction $Q\ :\ t\mapsto Q(t)$ vérifie l'équation différentielle $(E)\ :\  y'+(0.115)y=0.$

1. Résoudre l'équation $(E).$

2. a. Justifier que $Q(t)=1.4\mathrm{e}^{−0.115t}\;,\ T\geq 0.$

b. Donner le sens de variation de la fonction $Q.$

c. Résoudre dans $[0 \ ;\ +\infty[$ l'équation $Q(t)=0.7$ ; la solution sera arrondie à l'unité.

3. Pour une efficacité optimale de ce médicament, sa quantité présente dans le sang doit être comprise entre $0.7\,mg$ et $1.4\,mg.$

Expliquer pourquoi le médecin prescrit à ce patient une injection de $0.7\,mg$ chaque six heures.

Dans l'annexe ci-jointe $(O\;,\ \vec{i}\;,\ \vec{j})$ est un repère orthonormé du plan.

$\mathcal{C_{f}}$ est la représentation graphique de la fonction $f$ définie sur $\mathbb{R}$, par $f(x)=\dfrac{−x^{2}+x\ln x+x}{(x+1)^{2}}$ pour $x>0$ et $f(0)=0.$

Le réel $\alpha$ est l'abscisse du point d'intersection sur la courbe $\mathcal{C_{f}}$ avec l'axe des abscisses autres que le point $O.$

1. a. Par lecture graphique, donner le signe de $f(x).$

b. Montrer que $\ln\alpha=-(\alpha+1).$

2. On considère la fonction $g$ définie sur $[\alpha\ ;\ +\infty[$ par $f(x)=\dfrac{x\ln x}{x+1}+1$ et on désigne par $\mathcal{C_{f}}$ la courbe représentative de $g$ dans le repère $(O\;,\ \vec{i}\;,\ \vec{j}).$

Montrer que $\lim\limits_{x\rightarrow +\infty}g(x)=+\infty$ et que $\lim\limits_{x\rightarrow +\infty}\dfrac{g(x)}{x}=0$
            
3. a. Montrer que pour tout réel $x$ appartenant à l'intervalle $[\alpha\ ;\ +\infty[$, $g(x)=-\dfrac{f(x)}{x}$
 
b. Dresser le tableau de variation de $g.$
 
4. a. Montrer que $g(\alpha)=1-\alpha.$

b. Construire alors, sur l'annexe, le point de la courbe $\mathcal{C_{g}}$ d'abscisse $\alpha.$

c. Tracer la courbe $\mathcal{C_{g}}$

5. On désigne par $\mathcal{A}$ l'aire (en unité d'aire) de la partie du plan limitée par les courbes $\mathcal{C_{g}}$, $\mathcal{C_{f}}$ et les droites d'équations $x=\alpha$ et $x=1.$

a. Montrer, en utilisant une intégration par partie que
$$\int^{1}_{\alpha}f(x)\mathrm{d}x=-[xg(x)]_{\alpha}^{1}+\int^{1}_{\alpha}g(x)\mathrm{d}x$$

b. En déduire que $\mathcal{A}=\alpha^{2}-\alpha+1.$